Презентация на тему: Цилиндры и цилиндрические поверхности

Цилиндры и цилиндрические поверхности Геометрия 11 класс Р.О.Калошина, ГОУ лицей №533

План урока Цилиндрическая поверхность Сечение круговой цилиндрической поверхности Уравнение круговой цилиндрической поверхности Понятие цилиндра Круговой цилиндр Прямой круговой цилиндр Диктант Ответы
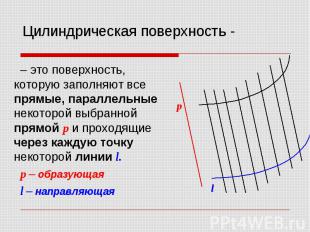
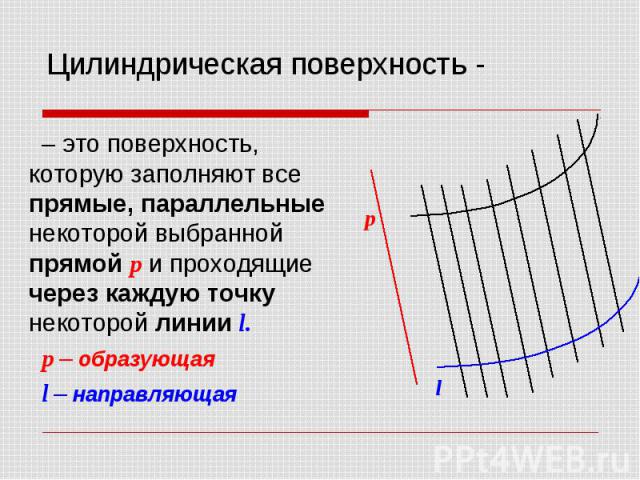
Цилиндрическая поверхность - – это поверхность, которую заполняют все прямые, параллельные некоторой выбранной прямой p и проходящие через каждую точку некоторой линии l. p – образующая l – направляющая
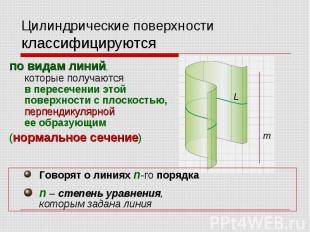
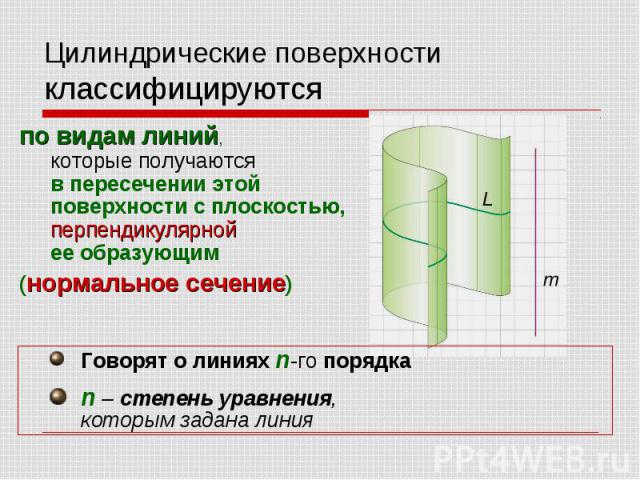
Цилиндрические поверхности классифицируютсяпо видам линий, которые получаются в пересечении этой поверхности с плоскостью, перпендикулярной ее образующим (нормальное сечение) Говорят о линиях n-го порядка n – степень уравнения, которым задана линия

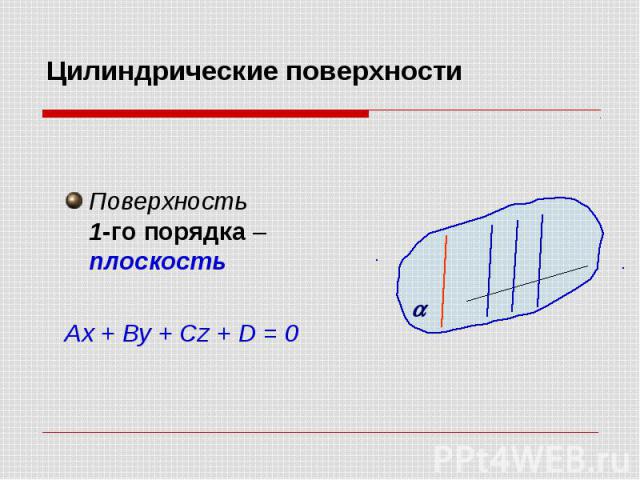
Цилиндрические поверхности Поверхность 1-го порядка – плоскость Ax + By + Cz + D = 0
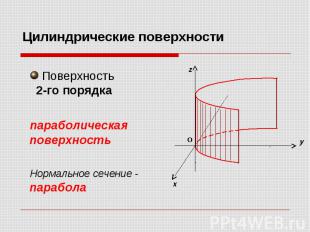
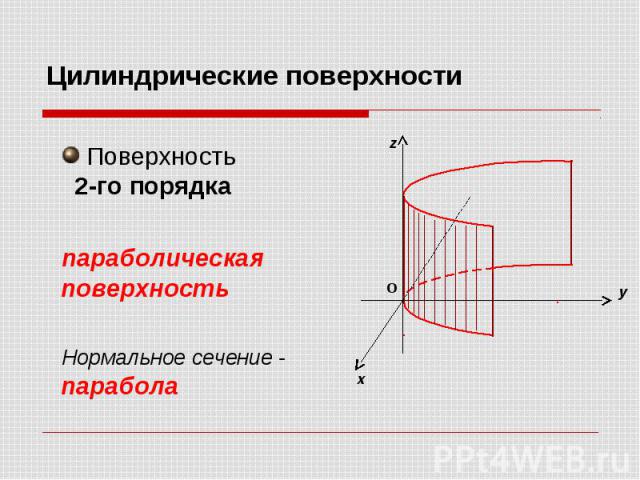
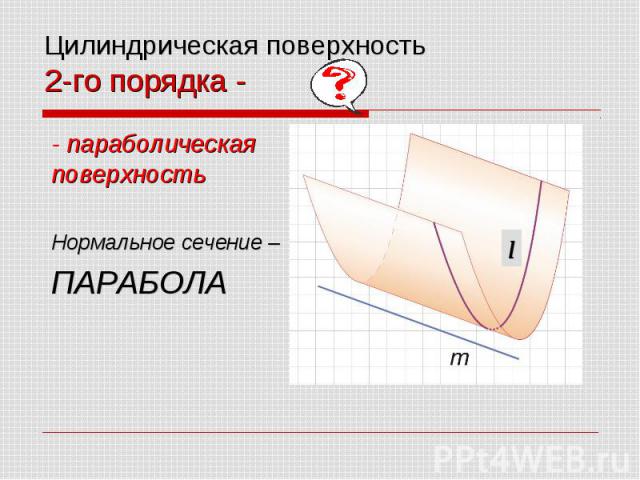
Цилиндрические поверхности Поверхность 2-го порядка параболическая поверхность Нормальное сечение - парабола
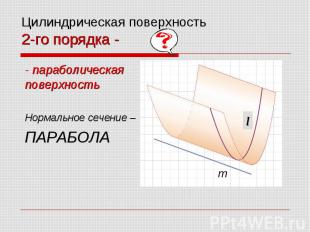
Цилиндрическая поверхность 2-го порядка - - параболическая поверхность Нормальное сечение – ПАРАБОЛА
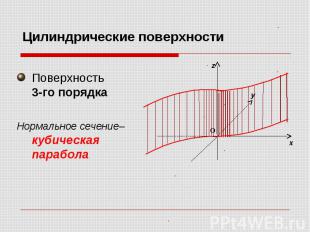
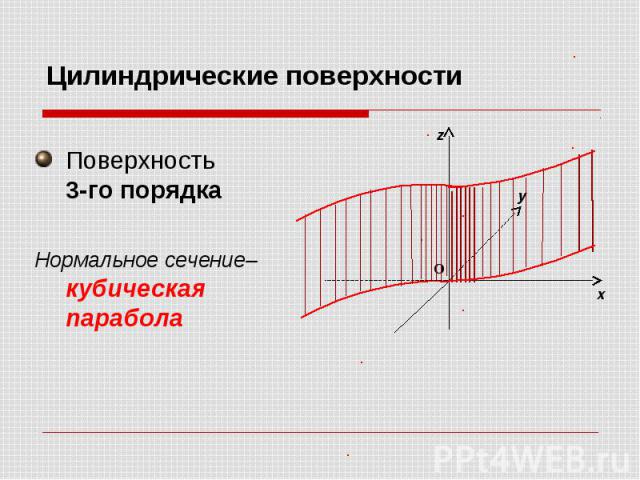
Цилиндрические поверхности Поверхность 3-го порядка Нормальное сечение– кубическая парабола

Круговая цилиндрическая поверхность – поверхность 2-го порядка получена вращением прямой l вокруг параллельной ей оси m. Нормальное сечение – окружность Круговая цилиндрическая поверхность, как и порождающая ее прямая, бесконечна в обе стороны.
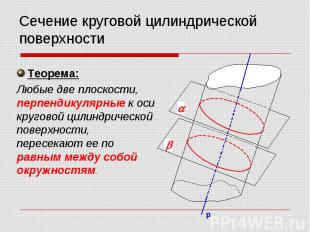
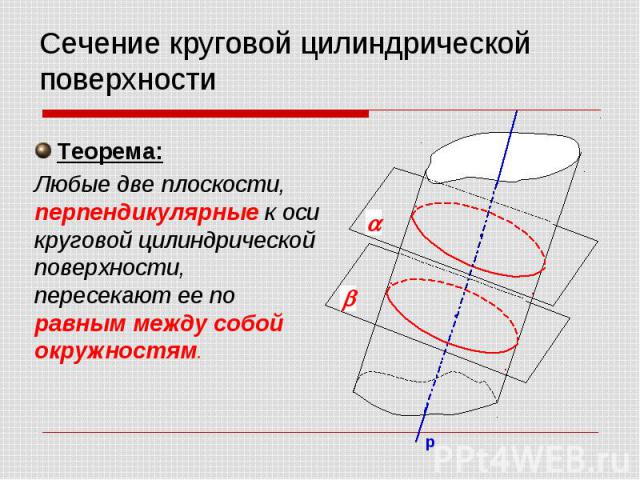
Сечение круговой цилиндрической поверхности Теорема: Любые две плоскости, перпендикулярные к оси круговой цилиндрической поверхности, пересекают ее по равным между собой окружностям.
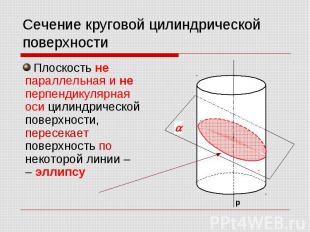
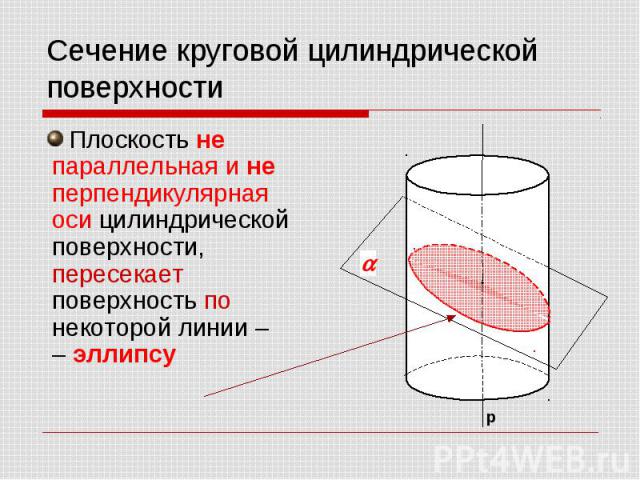
Сечение круговой цилиндрической поверхности Плоскость не параллельная и не перпендикулярная оси цилиндрической поверхности, пересекает поверхность по некоторой линии – – эллипсу
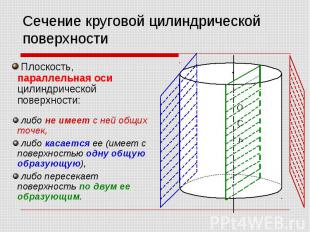
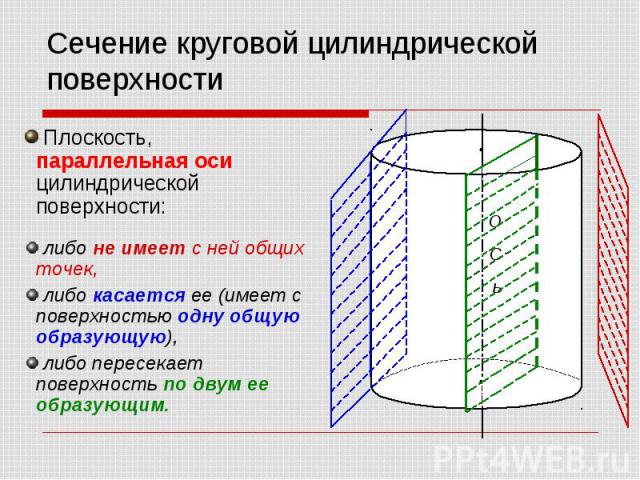
Сечение круговой цилиндрической поверхности Плоскость, параллельная оси цилиндрической поверхности: либо не имеет с ней общих точек, либо касается ее (имеет с поверхностью одну общую образующую), либо пересекает поверхность по двум ее образующим.
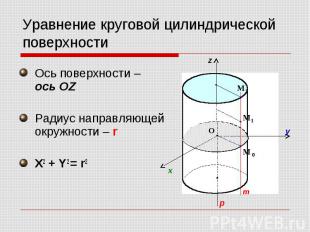
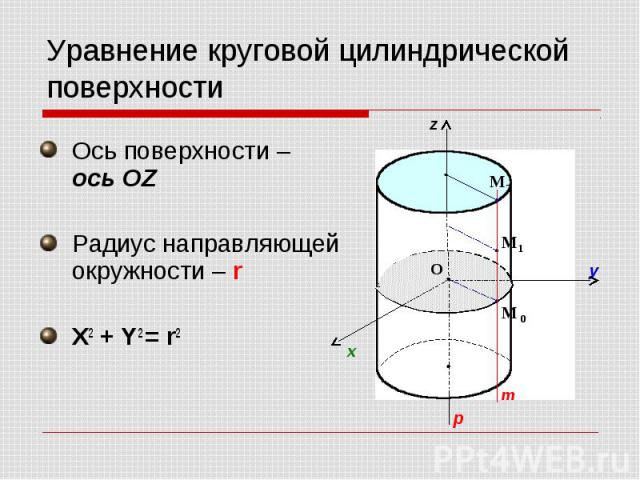
Уравнение круговой цилиндрической поверхности Ось поверхности – ось OZ Радиус направляющей окружности – r X2 + Y2 = r2

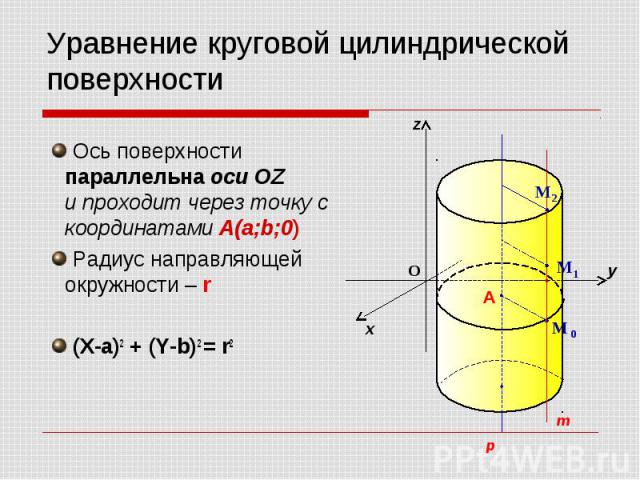
Уравнение круговой цилиндрической поверхности Ось поверхности параллельна оси OZ и проходит через точку с координатами A(a;b;0) Радиус направляющей окружности – r (X-a)2 + (Y-b)2 = r2
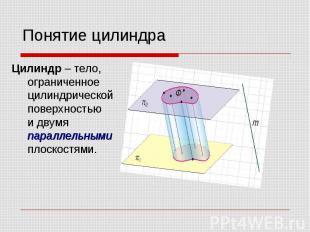
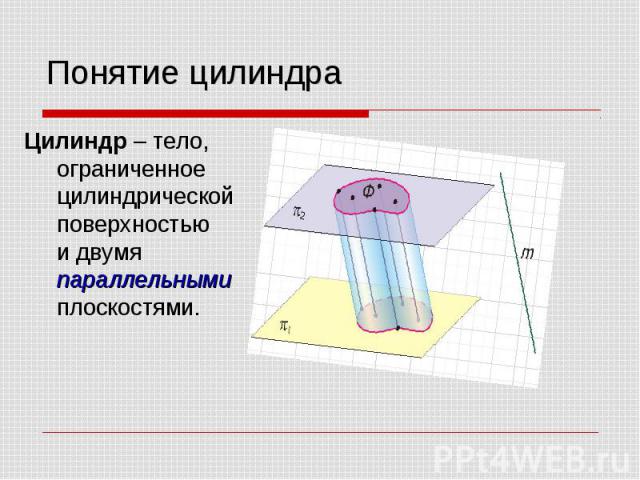
Понятие цилиндра Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями.

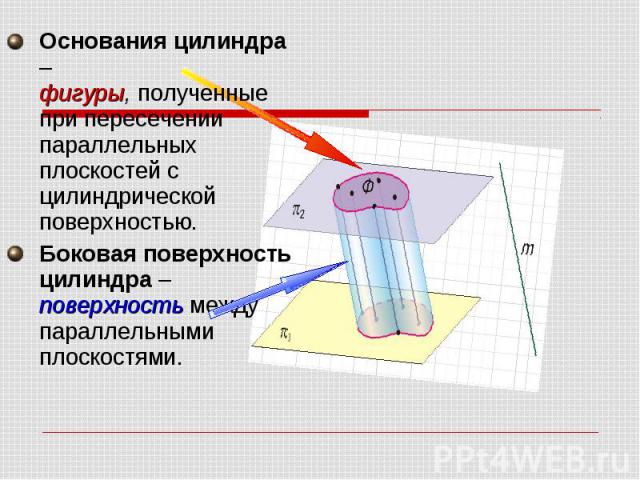
Основания цилиндра – фигуры, полученные при пересечении параллельных плоскостей с цилиндрической поверхностью. Боковая поверхность цилиндра – поверхность между параллельными плоскостями.
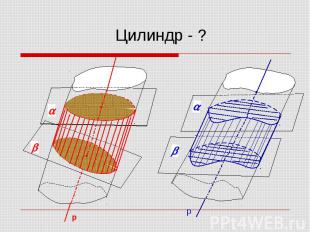
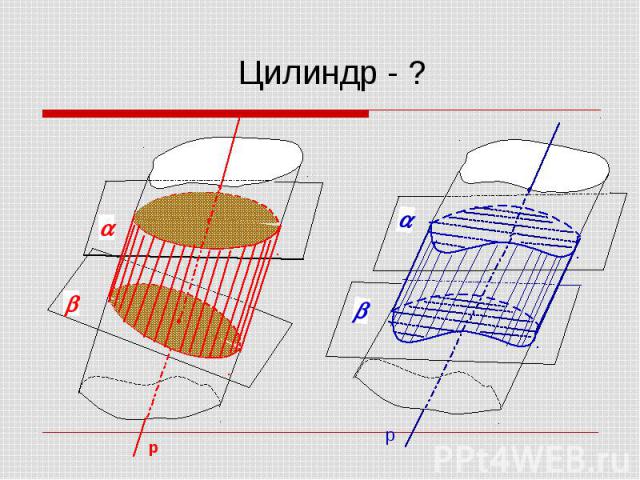
Цилиндр - ?
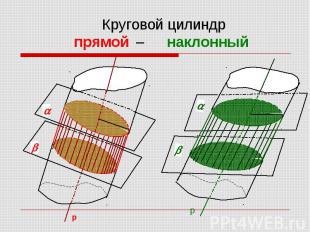
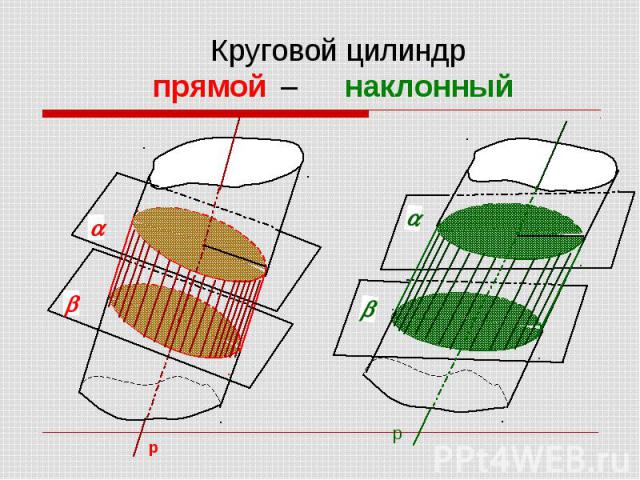
Круговой цилиндр прямой – наклонный
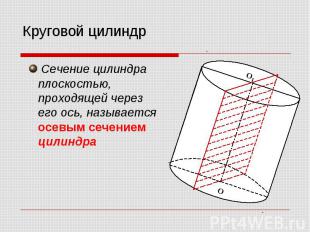
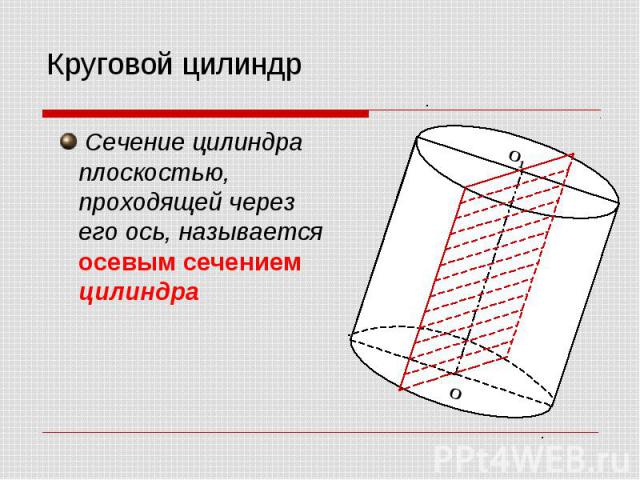
Круговой цилиндр Сечение цилиндра плоскостью, проходящей через его ось, называется осевым сечением цилиндра
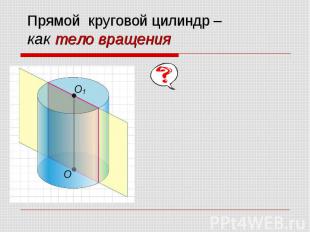
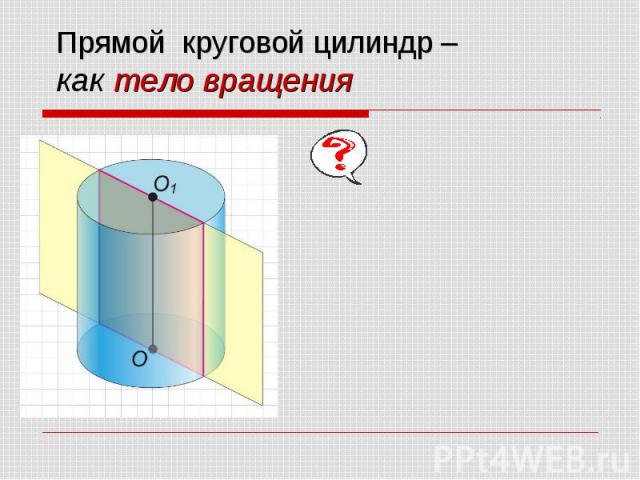
Прямой круговой цилиндр – как тело вращения
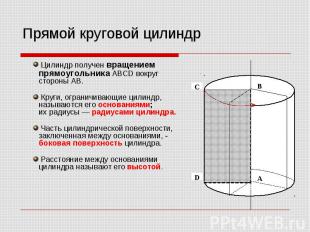
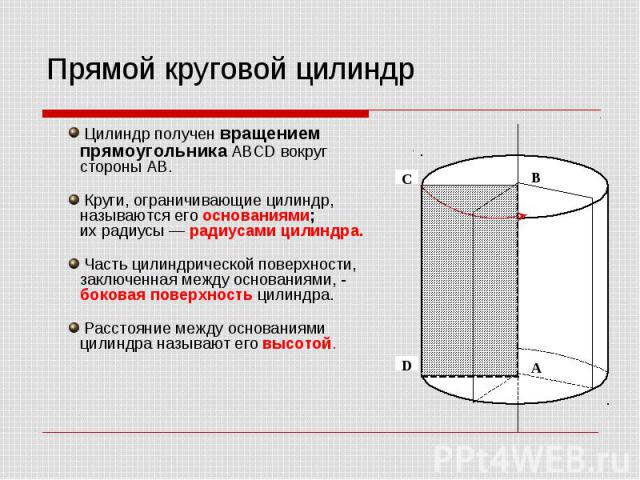
Прямой круговой цилиндр Цилиндр получен вращением прямоугольника ABCD вокруг стороны AB. Круги, ограничивающие цилиндр, называются его основаниями; их радиусы — радиусами цилиндра. Часть цилиндрической поверхности, заключенная между основаниями, - боковая поверхность цилиндра. Расстояние между основаниями цилиндра называют его высотой.
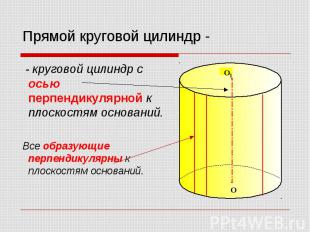
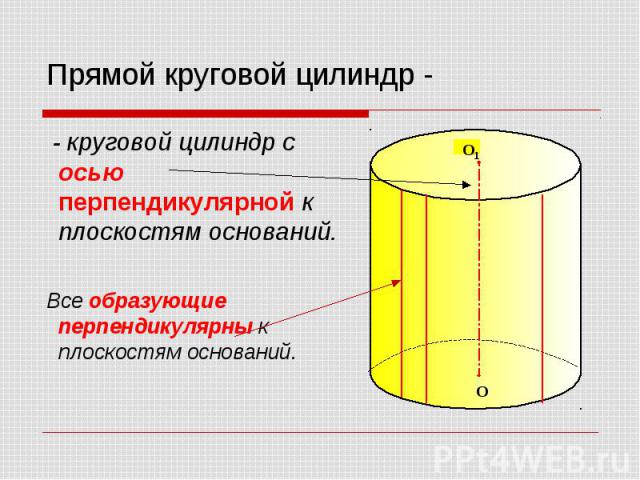
Прямой круговой цилиндр - - круговой цилиндр с осью перпендикулярной к плоскостям оснований. Все образующие перпендикулярны к плоскостям оснований.
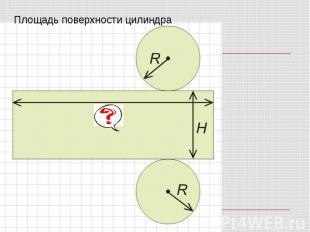
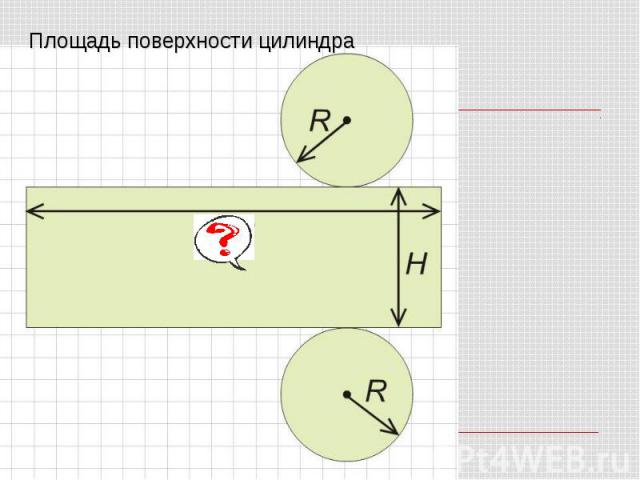
Площадь поверхности цилиндра

Тест (Ответ: 1 – «да»; 0 – «нет»)