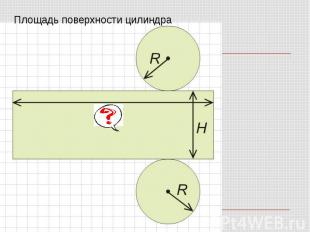
Презентация на тему: Цилиндры и цилиндрические поверхности

Цилиндрическая поверхность Цилиндрическая поверхность Сечение круговой цилиндрической поверхности Уравнение круговой цилиндрической поверхности Понятие цилиндра Круговой цилиндр Прямой круговой цилиндр Диктант Ответы

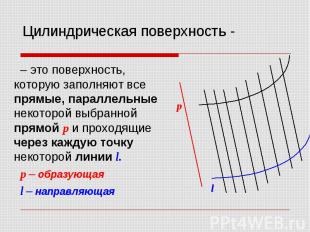
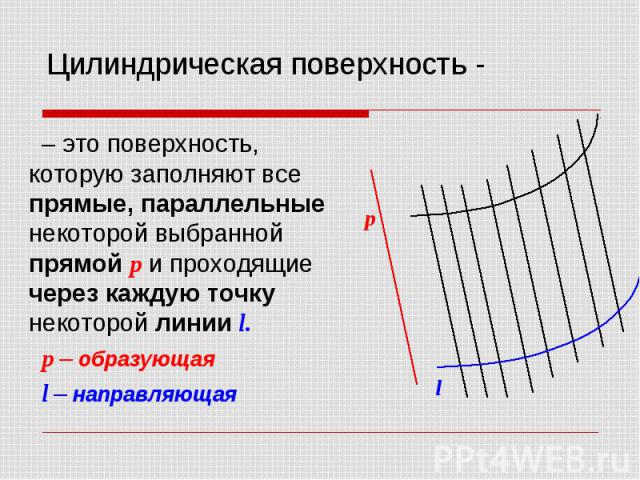
– это поверхность, которую заполняют все прямые, параллельные некоторой выбранной прямой p и проходящие через каждую точку некоторой линии l. – это поверхность, которую заполняют все прямые, параллельные некоторой выбранной прямой p и проходящие через каждую точку некоторой линии l. p – образующая l – направляющая

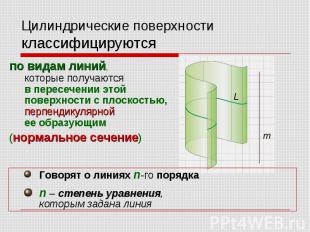
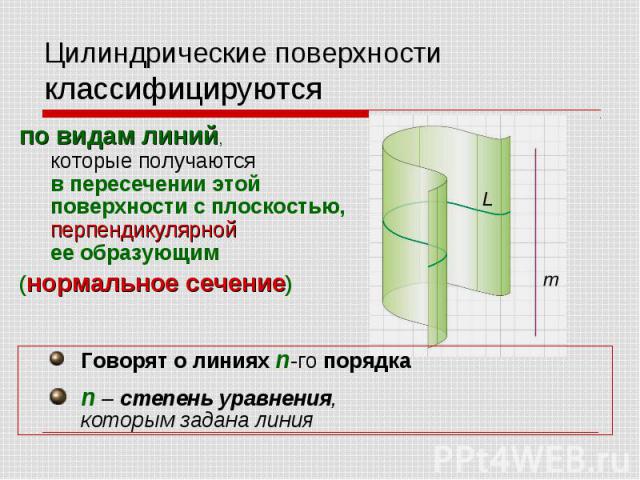
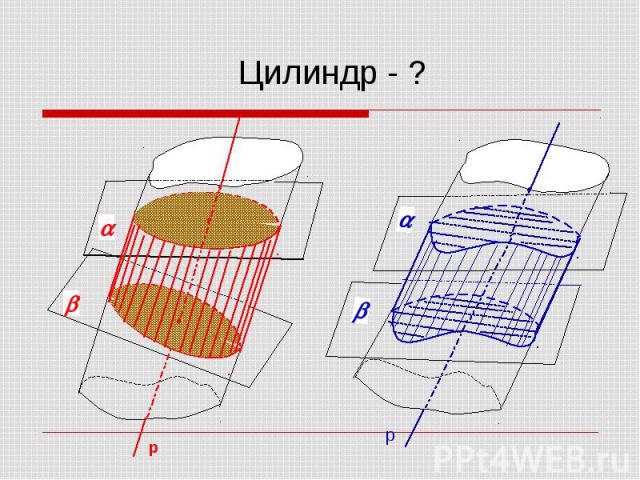
по видам линий, которые получаются в пересечении этой поверхности с плоскостью, перпендикулярной ее образующим по видам линий, которые получаются в пересечении этой поверхности с плоскостью, перпендикулярной ее образующим (нормальное сечение)

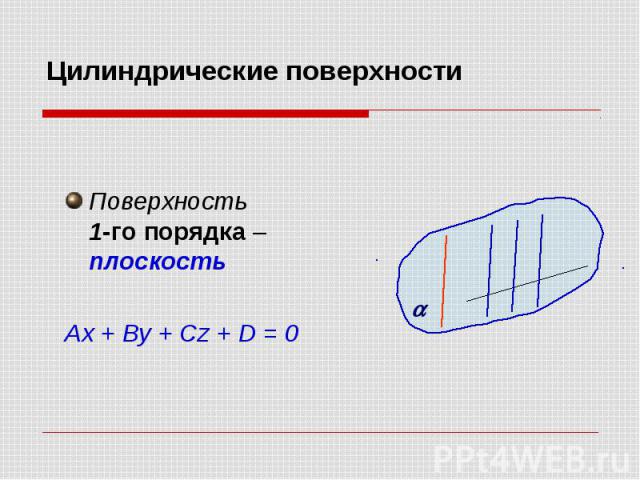
Поверхность 1-го порядка – плоскость Ax + By + Cz + D = 0

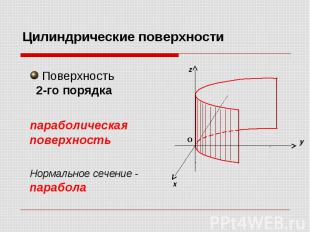
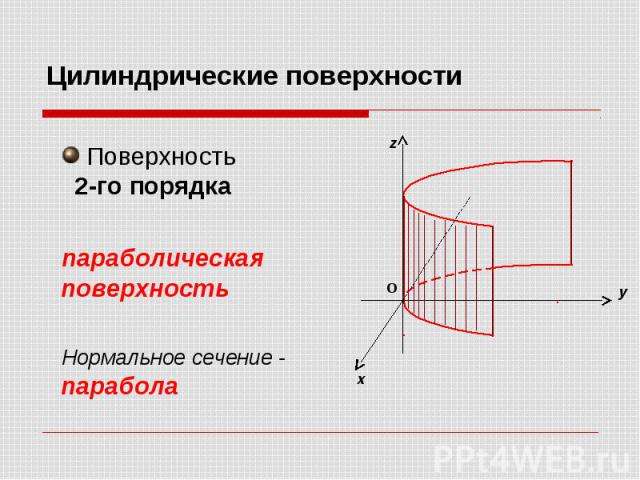
Поверхность 2-го порядка параболическая поверхность Нормальное сечение - парабола

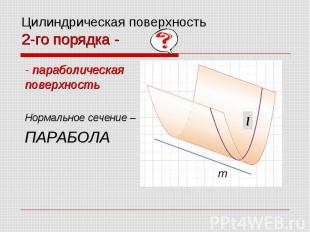
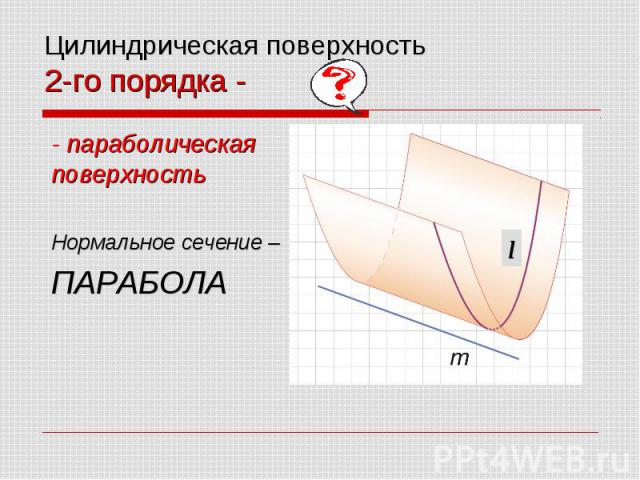
- параболическая поверхность - параболическая поверхность Нормальное сечение – ПАРАБОЛА

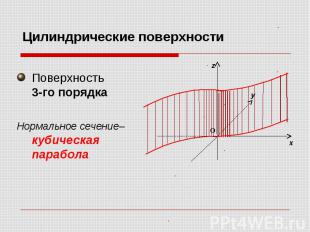
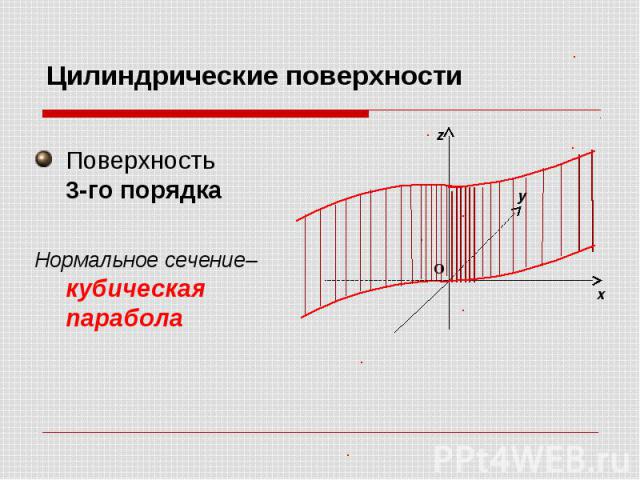
Поверхность 3-го порядка Нормальное сечение– кубическая парабола

получена вращением прямой l вокруг параллельной ей оси m. получена вращением прямой l вокруг параллельной ей оси m. Нормальное сечение – окружность

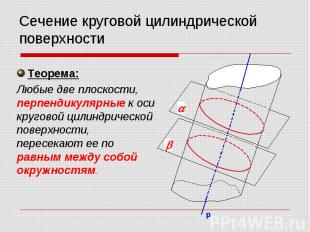
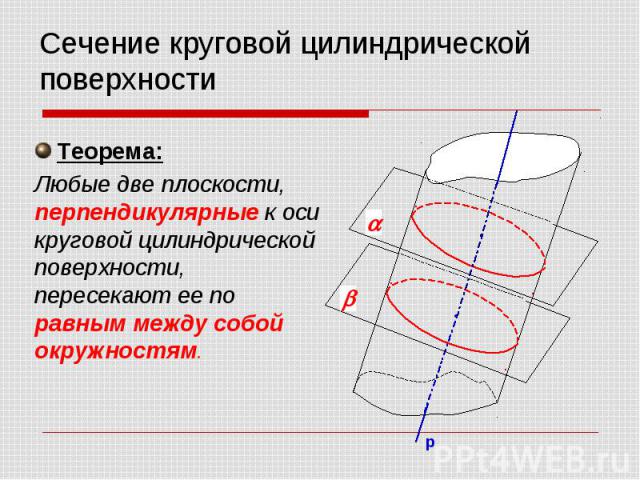
Теорема: Любые две плоскости, перпендикулярные к оси круговой цилиндрической поверхности, пересекают ее по равным между собой окружностям.

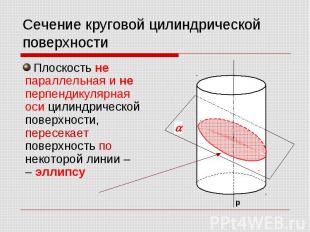
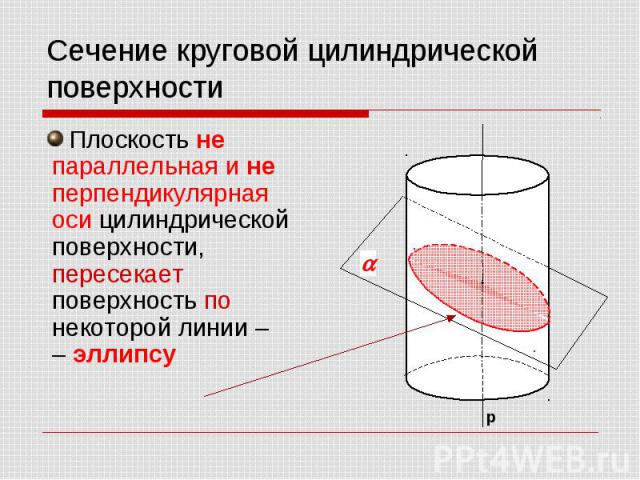
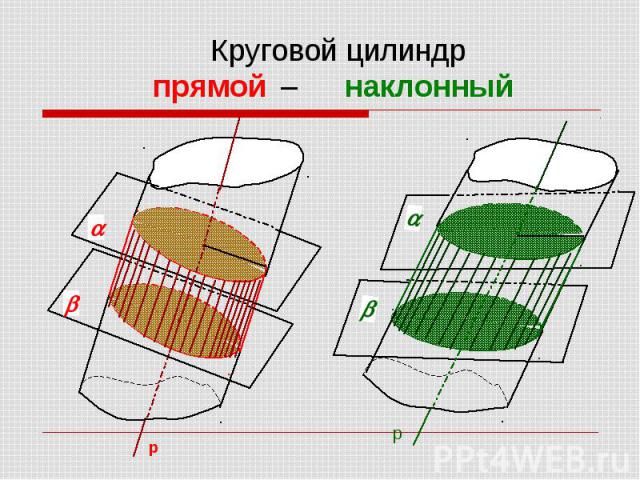
Плоскость не параллельная и не перпендикулярная оси цилиндрической поверхности, пересекает поверхность по некоторой линии – – эллипсу Плоскость не параллельная и не перпендикулярная оси цилиндрической поверхности, пересекает поверхность по некоторой линии – – эллипсу

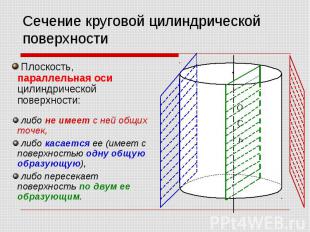
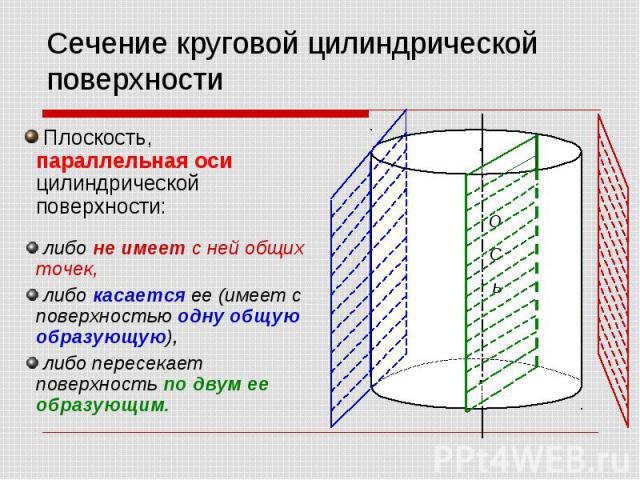
Плоскость, параллельная оси цилиндрической поверхности: Плоскость, параллельная оси цилиндрической поверхности: либо не имеет с ней общих точек, либо касается ее (имеет с поверхностью одну общую образующую), либо пересекает поверхность по двум ее образующим.

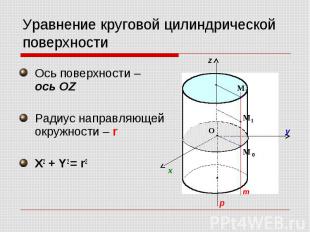
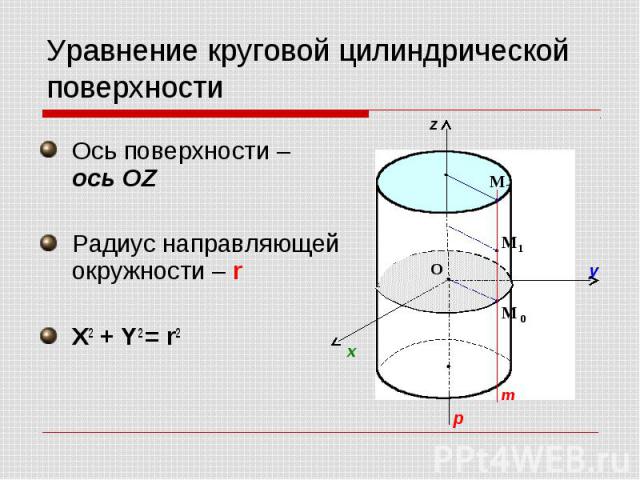
Ось поверхности – ось OZ Ось поверхности – ось OZ Радиус направляющей окружности – r X2 + Y2 = r2

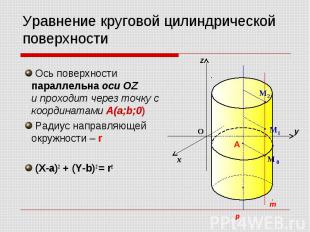
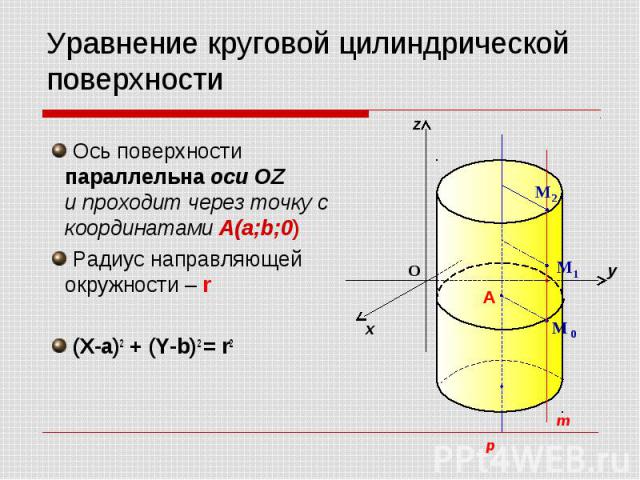
Ось поверхности параллельна оси OZ и проходит через точку с координатами A(a;b;0) Ось поверхности параллельна оси OZ и проходит через точку с координатами A(a;b;0) Радиус направляющей окружности – r (X-a)2 + (Y-b)2 = r2

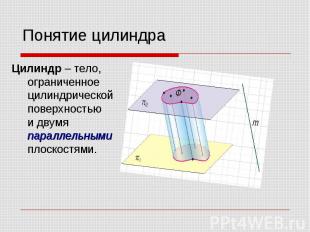
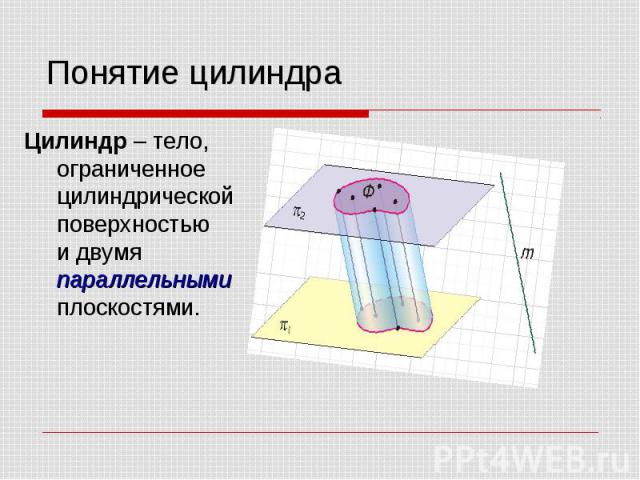
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями. Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями.

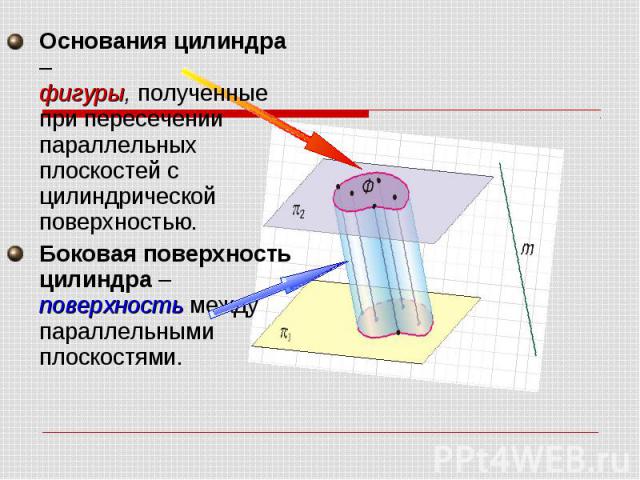
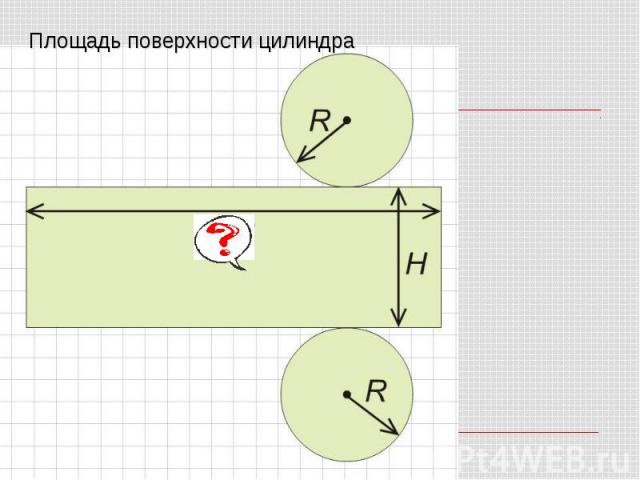
Основания цилиндра – фигуры, полученные при пересечении параллельных плоскостей с цилиндрической поверхностью. Основания цилиндра – фигуры, полученные при пересечении параллельных плоскостей с цилиндрической поверхностью. Боковая поверхность цилиндра – поверхность между параллельными плоскостями.

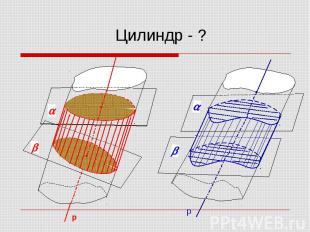
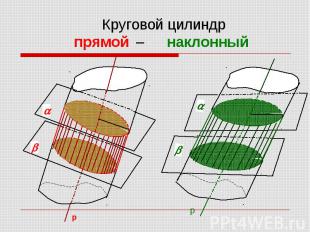
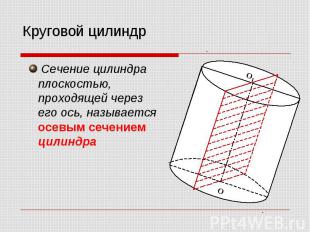
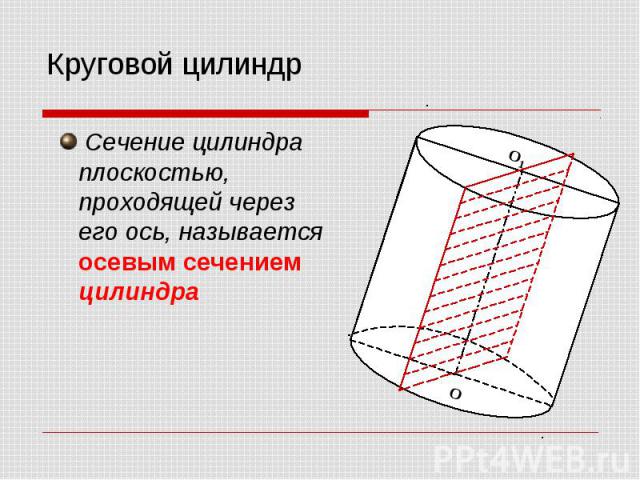
Сечение цилиндра плоскостью, проходящей через его ось, называется осевым сечением цилиндра Сечение цилиндра плоскостью, проходящей через его ось, называется осевым сечением цилиндра

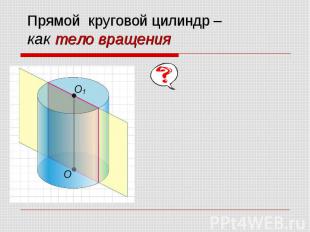
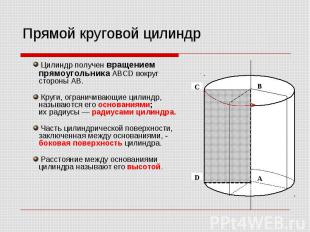
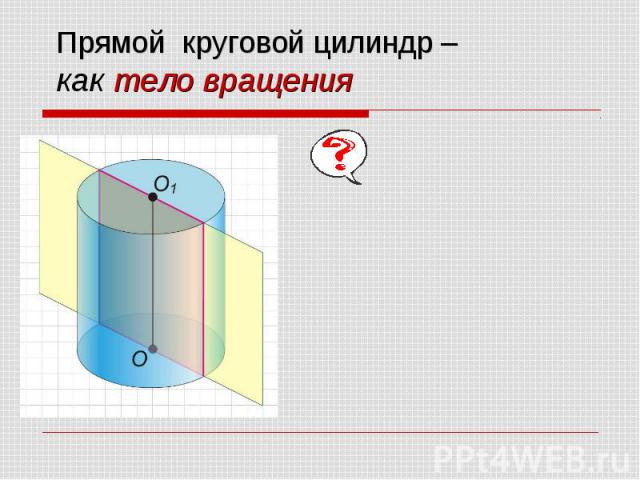
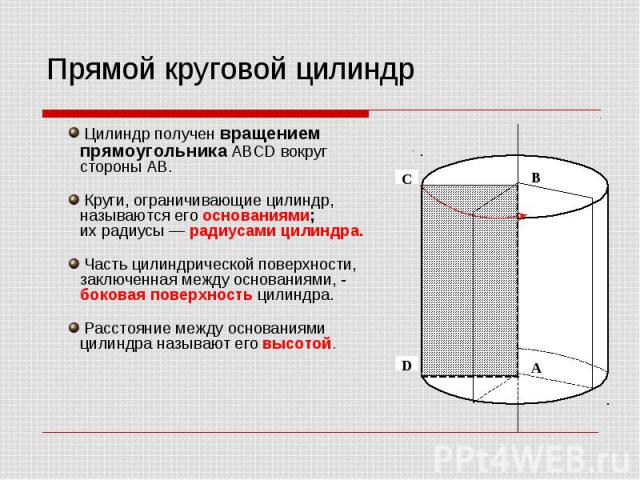
Цилиндр получен вращением прямоугольника ABCD вокруг стороны AB. Цилиндр получен вращением прямоугольника ABCD вокруг стороны AB. Круги, ограничивающие цилиндр, называются его основаниями; их радиусы — радиусами цилиндра. Часть цилиндрической поверхности, заключенная между основаниями, - боковая поверхность цилиндра. Расстояние между основаниями цилиндра называют его высотой.

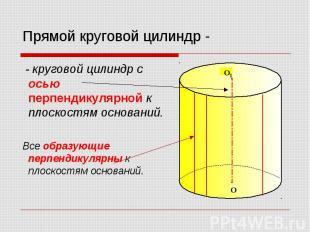
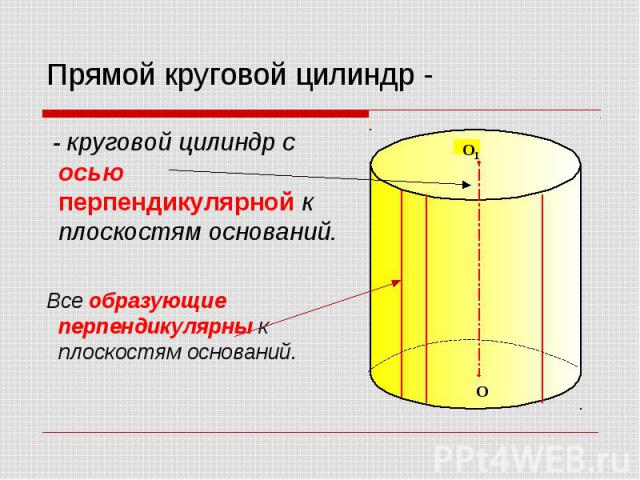
- круговой цилиндр с осью перпендикулярной к плоскостям оснований. - круговой цилиндр с осью перпендикулярной к плоскостям оснований. Все образующие перпендикулярны к плоскостям оснований.