Презентация на тему: Геометрия Лобачевского

МОУ Первоманская СОШ №2 Научно-исследовательская работа по математике на тему "Геометрия Лобачевского" Выполнил ученик 11 класса Баранов ОлегРуководитель: учитель математики Бунакова Ольга Николаевна

Гипотеза Многие математики, жившие после Евклида, пытались доказать, что эта аксиома (V постулат Евклида) – лишняя, т.е. она может быть доказана как теорема на основании остальных аксиом, но большинству из них так ничего и не удалось. Одним из тех, кто попытался сделать переворот в геометрии был Николай Иванович Лобачевский. Возможно, именно его геометрия способствовала бурному развитию современной геометрии.

Проблема: Большинство современных людей даже не знают о том, кто такой Николай Иванович Лобачевский и что он сделал для развития геометрии. Возможно они даже и не пытались узнать об этом. Эта работа поможет больше узнать о трудах этого человека, а кому-то углубить свои знания!

Цели: 1) Расширение знаний в области математики2) Закрепление навыков по созданию научно-исследовательских работ3) Выступление с научно-исследовательской работой на различных мероприятиях

Задачи: 1) Нахождение и обработка информации2) Создание научно-исследовательской работы3) Разработка стратегии выступлений

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, т. к. именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, общи обеим геометриям и образуют так называемую абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие отделы, включая тригонометрию и начала аналитической и дифференциальной геометрии.

Основное содержаниние" геометрии Лобачевского"

1) В Лобачевского геометрии не существует подобных, но неравных треугольников; треугольники равны, если их углы равны. Поэтому существует абсолютная единица длины, т. е. отрезок, выделенный по своим свойствам, подобно тому, как прямой угол выделен своими свойствами. Таким отрезком может служить, например, сторона правильного треугольника с данной суммой углов. 2) Сумма углов всякого треугольника меньше p и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность p — (a + b + g), где a, b, g — углы треугольника, пропорциональна его площади. 3) Через точку О, не лежащую на данной прямой а, проходит бесконечно много прямых, не пересекающих а и находящихся с ней в одной плоскости; среди них есть две крайние b, b', которые и называются параллельными прямой а в смысле Лобачевского. 4) Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.

5) Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом. 6) Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом. 7) Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии. 8) Длина окружности не пропорциональна радиусу, а растет быстрее. 9) Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии.

Применение "геометрии Лобачевского"

Сам Лобачевский применил свою геометрию к вычислению определённых интегралов. В теории функций комплексного переменного геометрия Лобачевского помогла построить теорию автоморфных функций. Связь с геометрией Лобачевского была здесь отправным пунктом исследований Пуанкаре, который писал, что «неевклидова геометрия есть ключ к решению всей задачи». Геометрия Лобачевского находит применение также в теории чисел, в её геометрических методах, объединённых под названием «геометрия чисел».

Была установлена тесная связь геометрии Лобачевского с кинематикой специальной (частной) теорией относительности .   Замечательное приложение геометрия Лобачевского нашла в общей теории относительности. Если считать распределение масс материи во Вселенной равномерным (это приближение в космических масштабах допустимо), то оказывается, что при определённых условиях пространство имеет геометрию Лобачевского. Таким образом, предположение Лобачевского о его геометрии как возможной теории реального пространства оправдалось.

Приложения(модели)

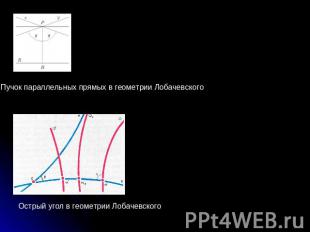
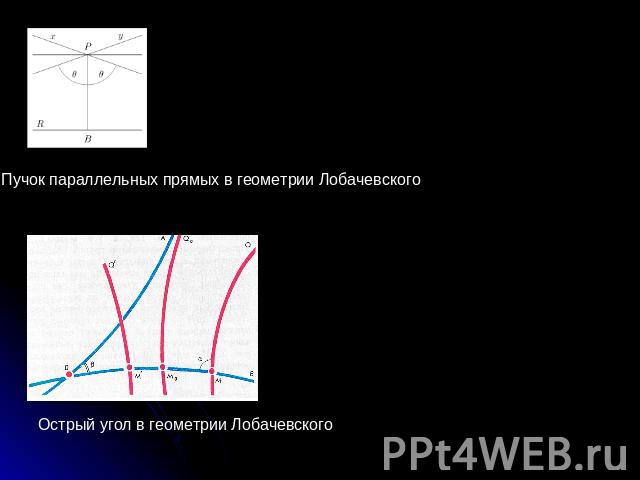
Пучок параллельных прямых в геометрии Лобачевского Острый угол в геометрии Лобачевского

В 1868 году итальянский математик Э.Бельстрами исследовал вогнутую поверхность, называемую псевдосферой, и доказал, что на этой поверхности действует геометрия Лобачевского! Расположения трех прямых на плоскости Лобачевского

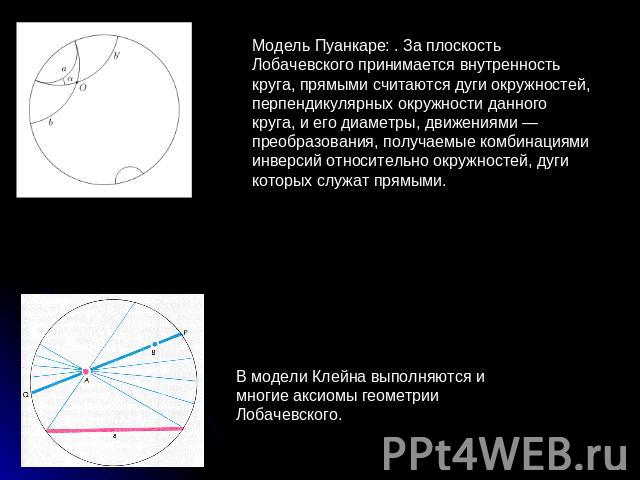
Модель Пуанкаре: . За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми. В модели Клейна выполняются и многие аксиомы геометрии Лобачевского.

Окружности Лобачевского в интерпретации Пуанкаре изображаются евклидовыми окружностями, целиком лежащими в верхней полуплоскости     Орициклы изображаются евклидовыми окружностями верхней полуплоскости, касающимися оси XX, при условии исключения точки касания

Литература: 1) А. Д. Александров, А. Л. Вернар, В. И. Рыжик, Геометрия М: Просвещение, 1991).2) Атанасян Л.С., Базылев В.Т. Геометрия. Ч.II. Просвещение, 19983) Каган В.Ф. Лобачевский. М., 1948. 4) www.yandex.ru5) Вахтин Б.М. Великий русский математик Н.И. Лобачевский. М., 1956 6) Широков П.А.: Краткий очерк основ геометрии Лобачевского.

СПАСИБО ЗА ВНИМАНИЕ!