Презентация на тему: Древняя геометрия

Геометрия в древней Греции Математика древней Греции прошла длительный и сложный путь развития, начиная с VI столетия до н.э. и по VI век. Историки науки выделяют три периода ее развития в соответствии с характером знаний: 1 - Накопление отдельных математических фактов и проблем (6 - 5B.B. до н.э.). 2 - Систематизация полученных знаний (4 - 3 в.в. до н.э.). 3 - Период вычислительной математики (3в. до н.э. - 6 в.).

еликие учёные древности

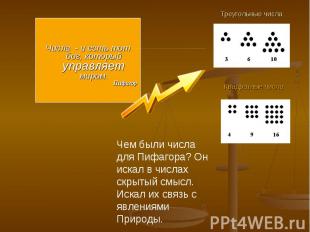
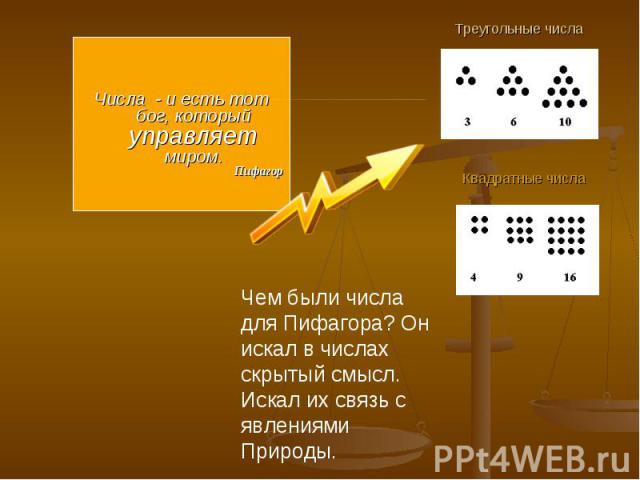
Треугольные числа Числа  - и есть тот бог, который управляет миром. Пифагор

Теорема Пифагора Теорема Пифагора гласит “в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов”.

гипетский треугольник Прямоугольные треугольники с целочисленными сторонами называют египетскими, а тройки целых чисел, для которых выполняется соотношение, связывающее стороны прямоугольного треугольника- пифагоровыми тройками

Фалес Милетский (625 – 547 гг. до н.э) История приписывает Фалесу следующие теоремы: круг делится диаметром пополам; углы при основании равнобедренного треугольника равны; противоположные углы между двумя пересекающимися прямыми (т.е. вертикальные углы) равны; если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (второй признак равенства треугольников); вписанный угол, опирающийся на диаметр, – прямой; если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки (теорема Фалеса).

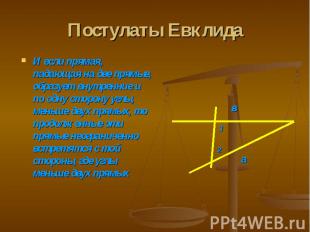
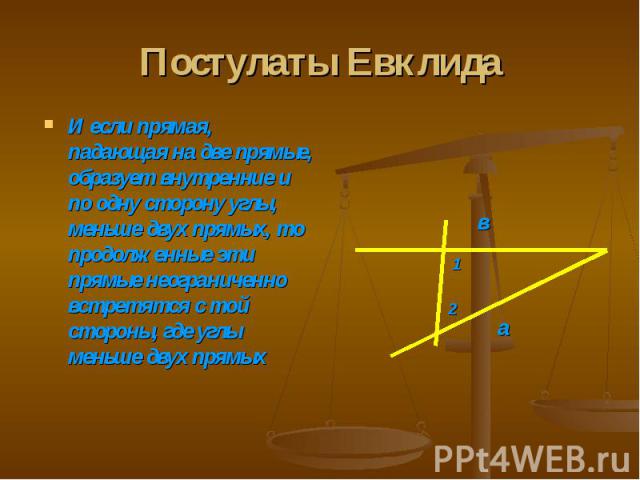
Постулаты Евклида И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньше двух прямых, то продолженные эти прямые неограниченно встретятся с той стороны, где углы меньше двух прямых

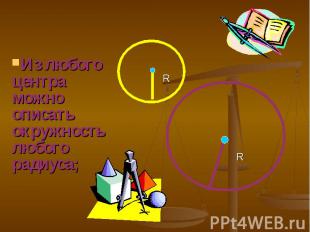
R R

Из каждой точки ко всякой другой точке можно провести прямую; Из каждой точки ко всякой другой точке можно провести прямую;

Каждую ограниченную прямую можно продолжить неопределённо; Каждую ограниченную прямую можно продолжить неопределённо;

Все прямые углы равны; Все прямые углы равны;