![Повторение: Ломаная АВС, где А ( 5; 1 ), В ( 3; 5 ), С ( 0; 0 ) – часть графика некоторой функции f ( x ). Область определения этой функции – промежуток [ -5; 5 ]. Постройте ее график, зная, что: I – f ( x ) – четная . II – f ( x ) – нечетная.](/images/51/1523/640/img4.jpg "Повторение: Ломаная АВС, где А ( 5; 1 ), В ( 3; 5 ), С ( 0; 0 ) – часть графика некоторой функции f ( x ). Область определения этой функции – промежуток [ -5; 5 ]. Постройте ее график, зная, что: I – f ( x ) – четная . II – f ( x ) – нечетная.")
Презентация на тему: Четные и нечетные функции
Четные и нечетные функции. МОУ СОШ №256 г.Фокино Каратанова Марина Николаевна
Повторение: Какая функция называется четной? Какая функция называется нечетной?
Повторение: Может ли быть четной или нечетной функция, областью определения которой является:
Повторение: Функция f (x) – четная, f ( 3 ) = 25 , тогда f ( -3 ) = ? f ( -8 ) = 71, тогда f ( 8 ) = ?
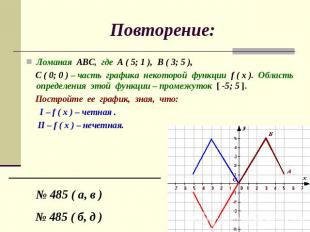
Повторение: Ломаная АВС, где А ( 5; 1 ), В ( 3; 5 ), С ( 0; 0 ) – часть графика некоторой функции f ( x ). Область определения этой функции – промежуток [ -5; 5 ]. Постройте ее график, зная, что: I – f ( x ) – четная . II – f ( x ) – нечетная.
Домашнее задание:№№ 515; 490; 492 ( б ).
Четные и нечетные функции.Математический диктант.
№ 1. Является ли функция четной или нечетной?
№ 2. I вариант. Каково свойство графика нечетной функции? II вариант. Каково свойство графика четной функции?
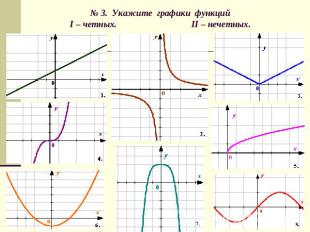
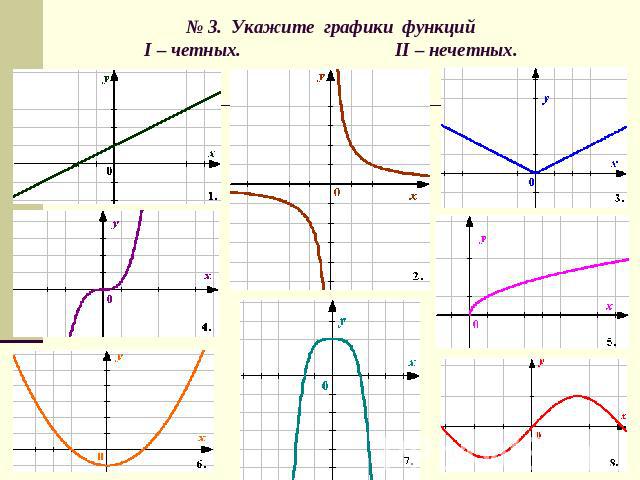
№ 3. Укажите графики функцийI – четных. II – нечетных.
