Презентация на тему: Четные и нечетные функции

Числовые функции.

Область определения функции Область значений функции Нули функции Интервалы знакопостоянства Интервалы монотонности Наибольшее и наименьшее значения Ограниченность функции Непрерывность Свойства функции

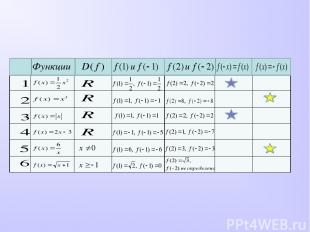
Проверка домашнего задания  Функции Область определения  Нули функции Координаты точек пересечения графика функции с Оy   Промежутки знакопостоянства  y > 0 y < 0                                  

Тема: Четные и нечетные функции сформулировать определение четности и нечетности функции; научиться определять и использовать чётность при исследовании функций и построении графиков. Цели:

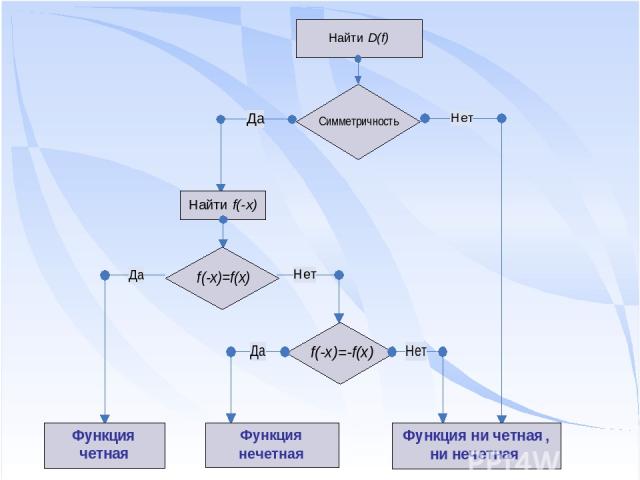
Функция y = f(x), заданная на множестве X называется четной, если для любого значения x из множества X выполняется равенство f(-x) = f(x). Функция y = f(x), заданная на множестве X называется нечетной, если для любого значения x из множества X выполняется равенство f(-x) = - f(x).

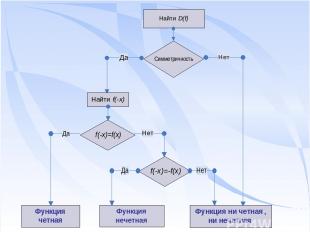
Алгоритм исследования функции на симметричность

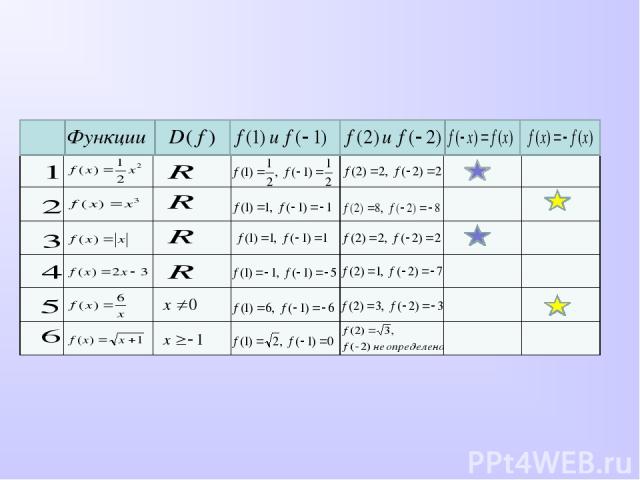
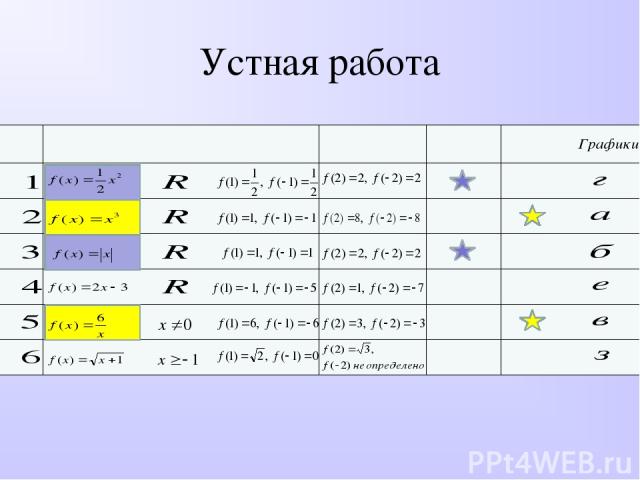
Устная работа                                                                                                                

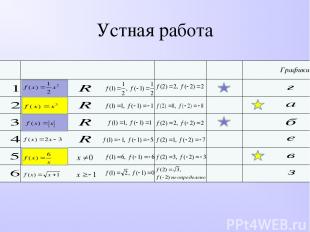
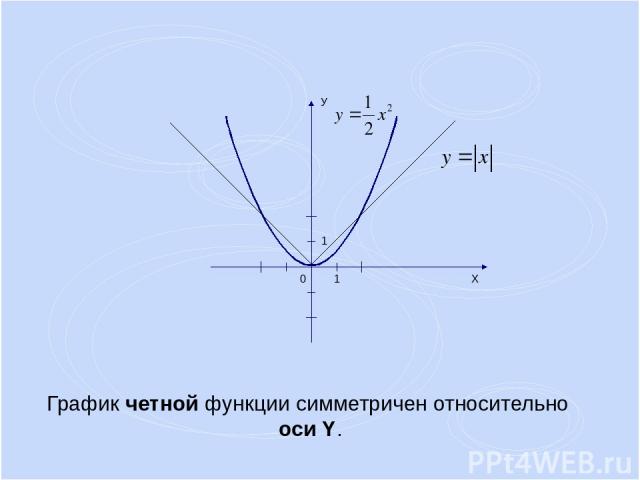
График четной функции симметричен относительно оси Y.

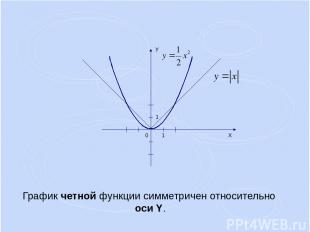
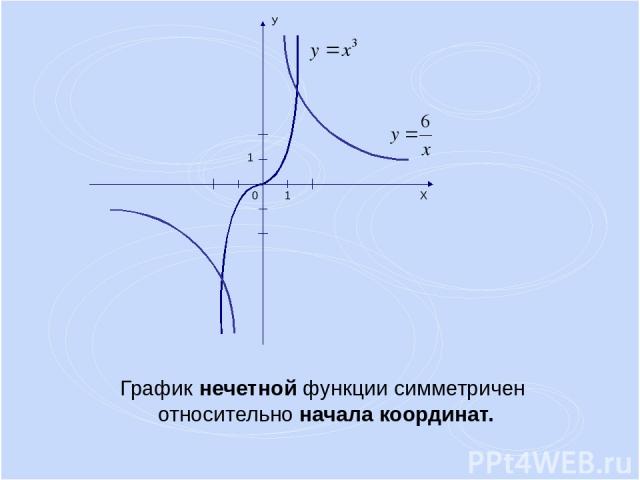
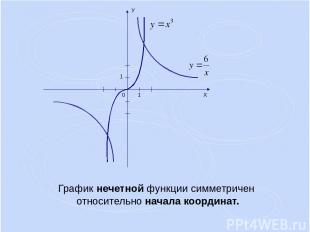
График нечетной функции симметричен относительно начала координат.

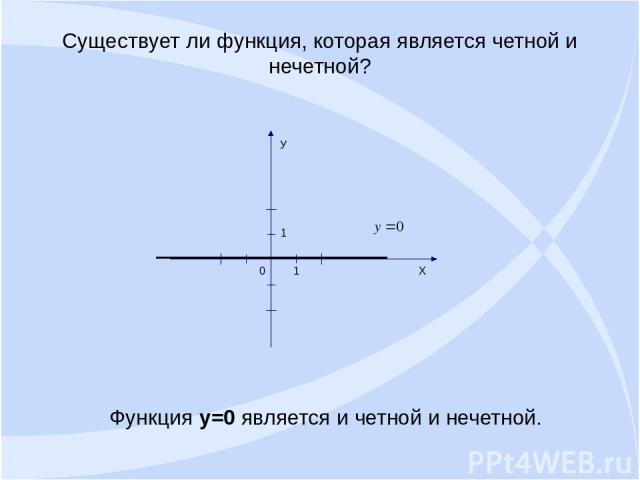
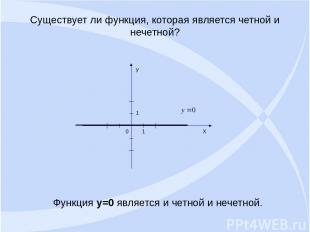
Существует ли функция, которая является четной и нечетной? Функция y=0 является и четной и нечетной.

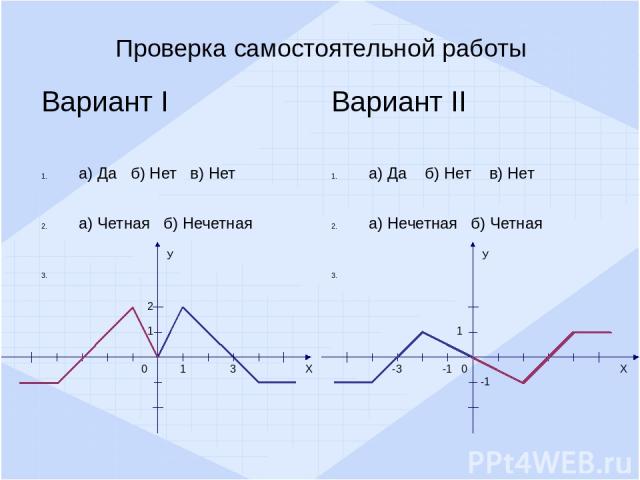
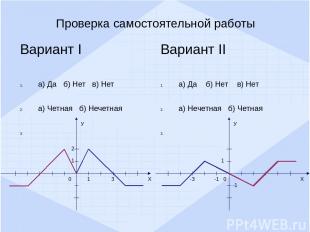
Вариант I а) Да б) Нет в) Нет а) Четная б) Нечетная Вариант II а) Да б) Нет в) Нет а) Нечетная б) Четная Проверка самостоятельной работы

№ 11.11, 11.21, 11.22; Доказать свойства чётности и нечётности (стр 114 учебника); ***(Задание из ЕГЭ ) Нечётная функция у = f(х) определена на всей числовой прямой. Для всякого неотрицательного значения переменной х значение этой функции совпадает со значением функции g (х) = х(х+1)(х+3)(х-7). Найдите значение функции при х=3. Домашнее задание

Подведение итогов