Презентация на тему: Прямоугольная декартова система координат

Прямоугольная декартова система координат

Тем, кто любит математику, Тем, кто знает математику, Тем, кто ещё не знает, Что он любит математику И тем, кто других учит математике Предназначена эта научно-практическая конференция «Известная и неизвестная прямоугольная система координат».

«То, что мы знаем – ограничено, а то, что мы не знаем – бесконечно…» французский математик и астроном Пьер-Симон Лаплас

Широта – параллели, долгота - меридианы Система географических координат Нанесенные на глобусы и карты параллели и меридианы составляют градусную сетку.

Участники конференции Секция лингвистики: «Толкование происхождения слов, связанных с декартовой системой координат» Секция истории: «История возникновения системы координат» Секция математики: «Декартовы координаты в пространстве» Секция прикладной математики: «Метод координат и его применение к решению задач» Секция искусствоведов: «Декартовы координаты в искусстве» Отдел практики: «Я расскажу вам о своей работе…» (о профессиях, использующих в своей работе теорию о системе координат)

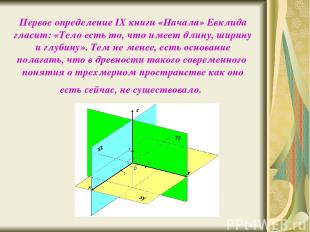
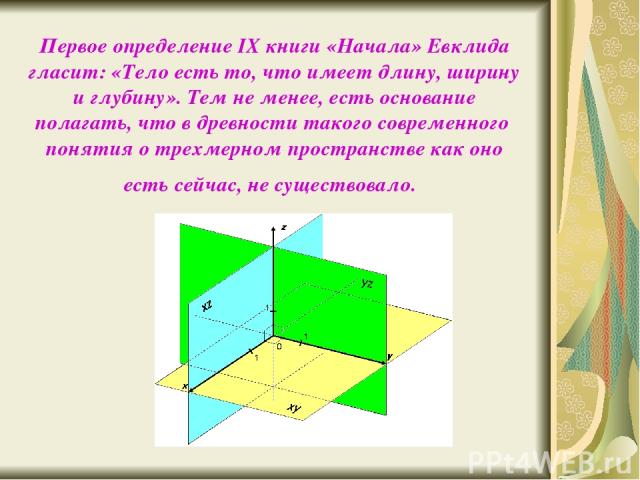
Первое определение IX книги «Начала» Евклида гласит: «Тело есть то, что имеет длину, ширину и глубину». Тем не менее, есть основание полагать, что в древности такого современного понятия о трехмерном пространстве как оно есть сейчас, не существовало.

История возникновения координат и системы координат начинается давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Изображать числа в виде точек, а точкам давать числовые обозначения было желанием ещё античной геометрии. Уже во II веке древнегреческий астроном Клавдий Птоломей пользовался широтой и долготой в качестве координат. Но, конечно же, основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту. Клавдий Птоломей Пьер Ферма Рене Декарт

Высь, ширь, глубь. Лишь три координаты. Мимо них где путь? Засов закрыт. С Пифагором слушай сфер сонаты, Атомам дли счёт, как Демокрит. Валерий Брюсов.

«Математика – мощный и универсальный метод познания природы, образец для других наук». Рене Декарт

В 1637 г. во Франции вышла книга, которая принесла её автору невероятную известность. По обычаям того времени она имела довольно длинное название: «Рассуждение о методе, позволяющем направлять разум и отыскивать истину в науках. Кроме того, Диоптрика, Метеоры и Геометрия, которые являются приложениями этого метода». Автор книги был Рене Декарт. Первые строки книги «Рассуждение о методе…» были такие слова Декарта: «Я мыслю, следовательно, я существую».

В декартовой системе координат получили реальное истолкование отрицательные числа.   Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Рене Декарт и Пьер Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

- Назовите координаты точек, лежащих на координатных осях. Какие из данных точек лежат на координатных осях и на какой: А(5;0;0), В(-7;5;0), С(0;0;-9), М(0;8;0), Р(0;1;0)? - Назовите координаты точек, лежащих в координатных плоскостях. Какие из данных точек лежат в координатных плоскостях и в какой: А(3;0;5), В(-1; 4; 6), С(0;5;-9), М(5;5;0), Х(9;7;0)? - Назовите координаты точки, совпадающей с началом координат; лежащей в пространстве. Выбрать среди заданных точек те, которые лежат в пространстве или в начале координат: А(0;7;-2), О (0;0;0), В(2;4;-4), М(8;-5;2), Р(0;0;0). Как определить положение точки в пространстве?

Письменно: решить задачу 1) Дано: А (1;-1;2), В (3;1;-2) Найдите координаты середины отрезка АВ и его длину. 2) Подготовка к ЕНТ (сб. тестов НЦТ 2009 год, В 3 № 24) Найти координаты центра тяжести треугольника с вершинами в точках А(3; -4; 7), В(-5; 3; -2) и С(8; 7; -8). А. (-2; -2; 1), В. (-5; 3; 9), С. (2; 2; 1), D. (2; 2; -1), Е. (2; -2; -1).

Из планиметрии мы знаем, что центр тяжести треугольника, указанного в условии задачи, находится в точке пересечения его медиан. Из элементарной геометрии известно, что три медианы треугольника пересекаются в одной точке, причем эта точка делит медианы в отношении 2:1, считая от вершины треугольника.

Координаты центра тяжести однородной треугольной пластинки, если не учитывать ее толщину, равны среднему арифметическому однородных координат ее вершин. Координаты центра тяжести треугольника, расположенного в пространстве будут находиться по формулам: ХЕ = УЕ = ZЕ = Z1 + Z2 + Z3 3

Подготовка к ЕНТ (сб. апробационных тестов НЦТ 2013 год, В 0173 № 24) Найти координаты центра тяжести треугольника с вершинами в точках А(7; -4), В(-1; 8) и С(-12; -1). А. (2; 1), В. (-2; 1), С. (3; -2), D. (-1; 2), Е. (2,5; 3). Ответ: В.(-2; 1)

Работа с учебником: решение задач № 4 стр. 68; дополнительно: № 9 стр. 68

Интересные факты о Рене Декарте. Немалой заслугой Декарта было введение удобных обозначений, сохранившихся до наших дней: латинских букв x, y, z - для неизвестных; a, b, c - для коэффициентов, x2, y5, a7- для степеней. Основное новшество Декарта - введение переменных величин как координатных отрезков переменной длины. Идея геометрии Декарта состоит в том, что геометрический объект задается уравнением, связывающим переменные величины. По свойствам уравнения судят о свойствах геометрического объекта. Декарт считается одним из основателей новой математики. Его имя сохранили термины: «декартовы координаты», «декартов лист», «правило знаков Декарта», «метод неопределенных коэффициентов Декарта».

Интересен тот факт, что Рене Декарт увлекался не только математикой как наукой. Он увлекался науками от медицины до метеорологии. Его многочисленные труды были посвящены философии, астрономии, психологии, физиологии, физике и другим наукам. Декарт первый математически вывел закон преломления света (независимо от В. Снеллиуса) на границе двух различных сред. Точная формулировка этого закона позволила усовершенствовать оптические приборы, которые тогда стали играть огромную роль в астрономии и навигации. В честь Рене Декарта назван кратер на Луне. Великий физиолог И. П. Павлов поставил памятник-бюст   Рене Декарту возле своей лаборатории (Колтуши), потому что считал его предтечей своих исследований.

«В чистой математике живет всегда художник: архитектор и даже поэт». Томас Манн (А. Принсгейм)

Системы координат пронизывают всю практическую жизнь человека и находят свое применение почти в каждой специальности. Назовите те специальности, которые на ваш взгляд с своей работе используют теорию Рене Декарта.

Контрольные вопросы: - Объясните, как определяются координаты точки в пространстве. - Сколько чисел задают любую точку на плоскости, в пространстве? - Каким свойством обладают координаты точек, лежащих на координатных осях? - Каким свойством обладают координаты точек, лежащих в координатных плоскостях? С(0; 0; 8), D (-1;5;0), Е(0; 7;4), F(-6;-1; 0), К(0;0;0), М(0;-3;5), N(2;4;-1), Р(0;-6;0), А(1;0;5). Определите точки, принадлежащие: а) осям координат х, у, z; б) координатным плоскостям ху, хz, уz.

«Изучив столько всего, лишь теперь, уразумел я, что на самом деле не знаю ничего…» Омар Хайям