Презентация на тему: Определение двугранных углов

Цели урока: 1. Расширить понятие : «Угол» 2.Вывести определение двугранных углов. 3 . Научиться измерять двугранные углы 4. Научиться применять свойства двугранных углов при решении задач.

Углы выводим постепенно, по команде мышки, поэтому повторяем определение и свойства Линейный угол (острый, прямой, тупой) Вертикальные углы Смежные углы Центральный угол Вписанный угол.

А М Р

Перпендикуляр , наклонная и проекция. Теорема трёх перпендикуляров. Свойства наклонных и проекций. Повторить данные вопросы в задачах.

В С А К Н Перпендикуляр, наклонная и проекция связаны теоремой Пифагора Теорема трёх перпендикуляров для прямой КС. Плоскость АВС КС Равные наклонные имеют …….. Большая наклонная………

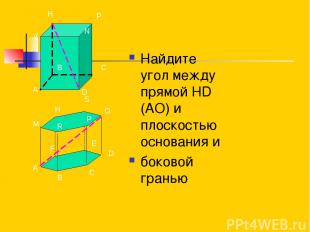
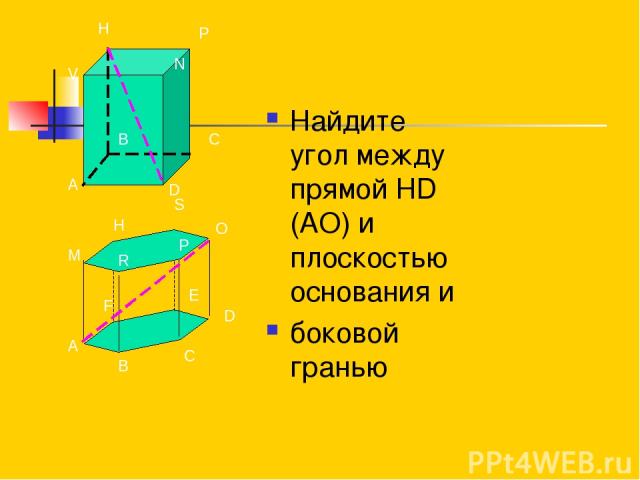
А В С D V H P N A B C D E F M H S O P R Найдите угол между прямой HD (AO) и плоскостью основания и боковой гранью

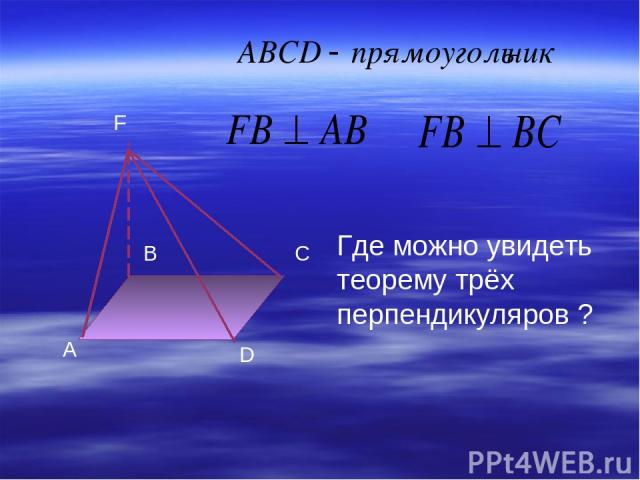
А D C B F Провести перпендикуляр к DC и AD из точки F ABCD –квадрат, ромб. Как связаны между собой перпендикуляр, наклонная и проекция наклонной?

A B C D F Где можно увидеть теорему трёх перпендикуляров ?

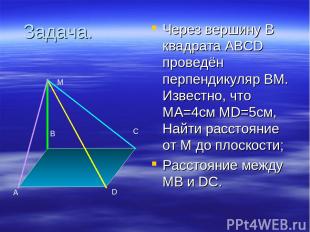
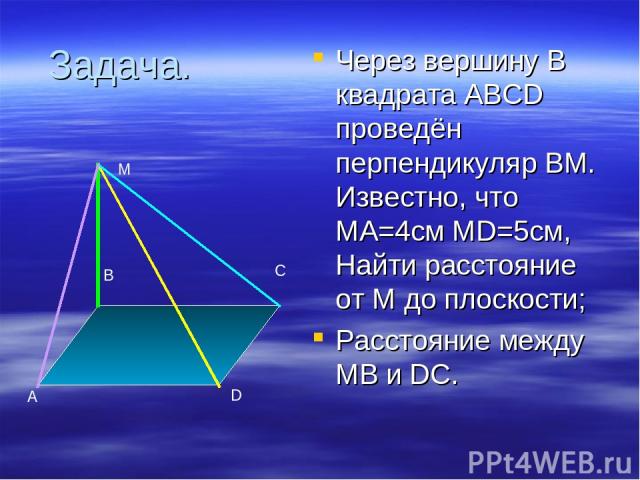
Задача. Через вершину В квадрата ABCD проведён перпендикуляр ВМ. Известно, что МА=4см MD=5см, Найти расстояние от М до плоскости; Расстояние между МВ и DC. A B C D M

Основная часть урока. Задания практические: Все взяли файловый лист, согнули на две неравные части , сделали вывод-две пересекающиеся полуплоскости с общей прямой называют двугранным углом. Как его измерить? Проведём общую прямую, вспомним аксиому плоскостей, Отметим на ребре точку. Проведём перпендикуляры к ребру из данной точки в каждой грани. Снова сгибаем по ребру и делаем вывод, что углы разные, значит их нужно отличать , как? Берём ножницы и делаем срез-щелку по перпендикулярам, вставляем лист в щелку и видим линейный угол. Просматриваем слайды , дающие ответы на полученные предложения. Даём определение измерения двугранных углов. Показываем двуг-е углы на моделях пирамид, призм и на таблицах.

Двугранные углы Известно, что мерой двугранного угла называют меру его линейного угла. Если на ребре двугранного угла отметить какую-нибудь точку в каждой грани из этой точки провести лучи перпендикулярно ребру, то получим линейный угол. М

М Точка на ребре может быть произвольная…

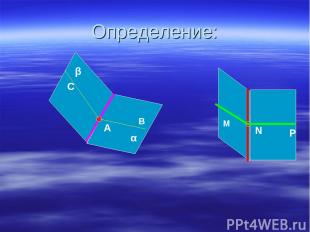
Определение: α β В А С М N P

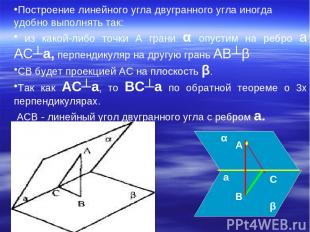
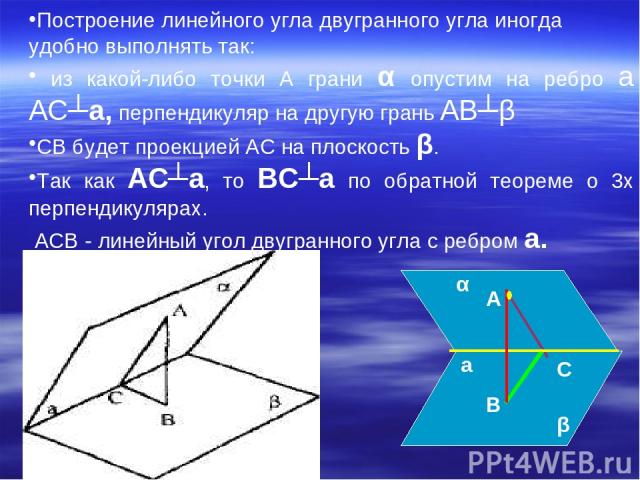
Построение линейного угла двугранного угла иногда удобно выполнять так: из какой-либо точки А грани α опустим на ребро а AC┴а, перпендикуляр на другую грань AB┴β СВ будет проекцией АС на плоскость β. Так как AC┴а, то BC┴а по обратной теореме о 3х перпендикулярах. ACB - линейный угол двугранного угла с ребром а. А В С а α β

Две пересекающиеся плоскости называются перпендикулярными, если угол между ними 90°.

Свойства: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то такие плоскости перпендикулярны.

Замечания к решению задач. Можно решать на компьютерах, используя «Автофигуры» Можно решать на «интердоске». Можно проецировать прямо на обычную доску или белую. Выводим на экран условия задачи и дорисовываем и решаем прямо на кадре. Каждый ученик может сохранить решение задачи, а учитель затем оценит. Можно вывести на общий экран решения учеников и рассмотреть разные способы.

В одной из граней двугранного угла, равного 30, расположена точка М. Расстояние от точки до ребра двугранного угла равно 18 см. Вычислите расстояние от проекции точки М на вторую грань до ребра двугранного угла. М

Отрезки АС и ВС, лежащие в гранях прямого двугранного угла, перпендикулярны к его ребру. Вычислите расстояние между точками А и В, если АС=10см, ВС=24см.

Точка К, в грани двугранного угла, удалена от другой грани на 12 см, а от ребра на Вычислить величину двугранного угла. К К К

На ребре двугранного угла, равного расположена точка А. В его гранях проведены перпендикуляры к ребру АВ и АС, равные соответственно 10 см, и 8см. Вычислите расстояние между точками В и С. А А В С

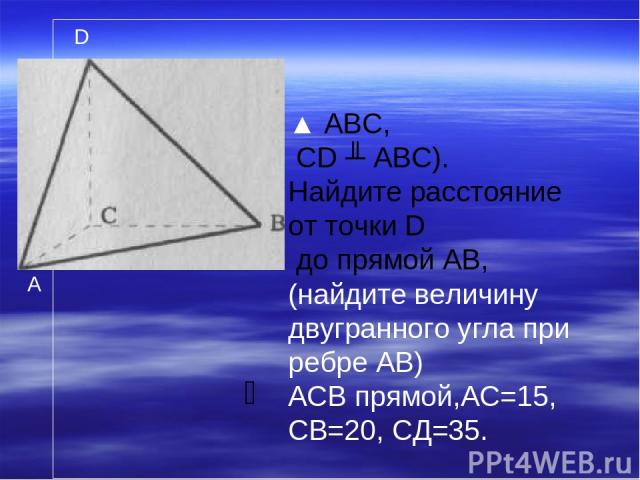
Найдите расстояние от точки D до прямой АВ, если АС = CB=10,AB=16, CD = 6. Изобразите перпендикуляр из точки D к прямой АВ. Найдите величину двугранного угла при ребре АВ. ▲ABC, CD╨ABC D

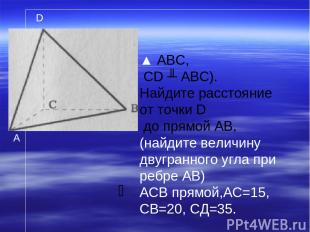
▲ ABC, CD ╨ ABC). Найдите расстояние от точки D до прямой АВ, (найдите величину двугранного угла при ребре АВ) АСВ прямой,АС=15, СВ=20, СД=35. A D

Точки М и К лежат в разных гранях прямого двугранного угла. Расстояние от этих точек до ребра равны 20см и 21 см. Вычислите расстояние между отрезками МК и ребром двугранного угла. М К

Концы отрезка лежат в гранях двугранного угла и удалены от его ребра на 6см и . Расстояние между данным отрезком и ребром равно 3 см. Вычислите величину двугранного угла.

Точка К удалена от каждой стороны равностороннего треугольника АВС на 8 см, АВ=24 см. Вычислите величину двугранного угла, ребром которого является прямая ВС, а грани содержат точки К и А. К А В С А В С

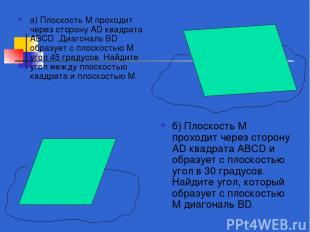
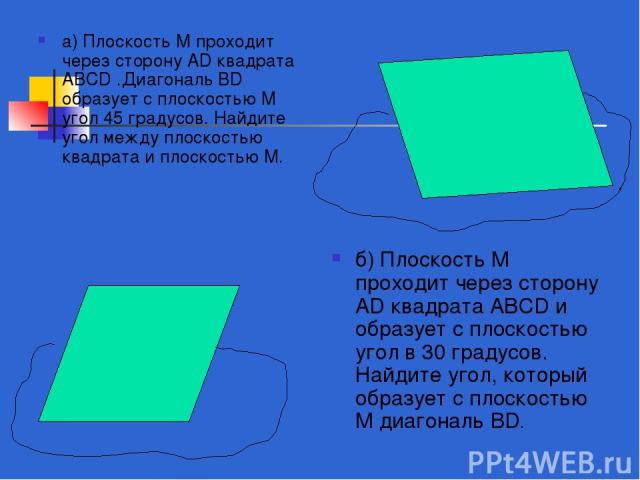
а) Плоскость М проходит через сторону AD квадрата ABCD .Диагональ BD образует с плоскостью М угол 45 градусов. Найдите угол между плоскостью квадрата и плоскостью М. б) Плоскость М проходит через сторону АD квадрата ABCD и образует с плоскостью угол в 30 градусов. Найдите угол, который образует с плоскостью М диагональ BD.

Основание пирамиды PABCD - прямоугольник ABCD , стороны которого равны Плоскости РАВ и РВС перпендикулярны плоскости АВС, а плоскость РАС наклонена к ней под углом . Найдите высоту и объём пирамиды.

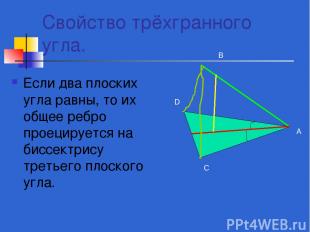
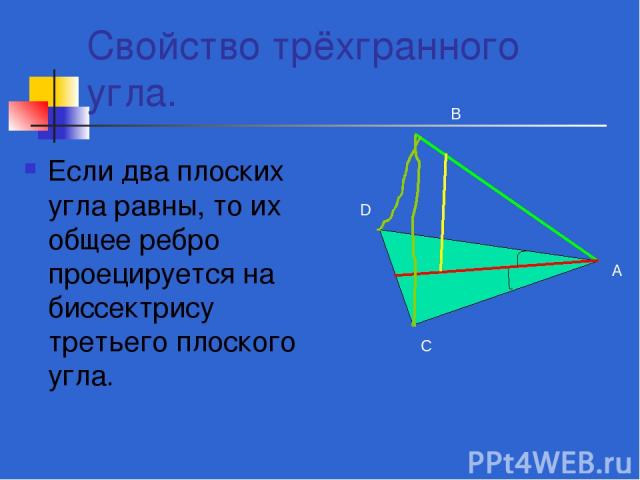
Свойство трёхгранного угла. Если два плоских угла равны, то их общее ребро проецируется на биссектрису третьего плоского угла. А В С D

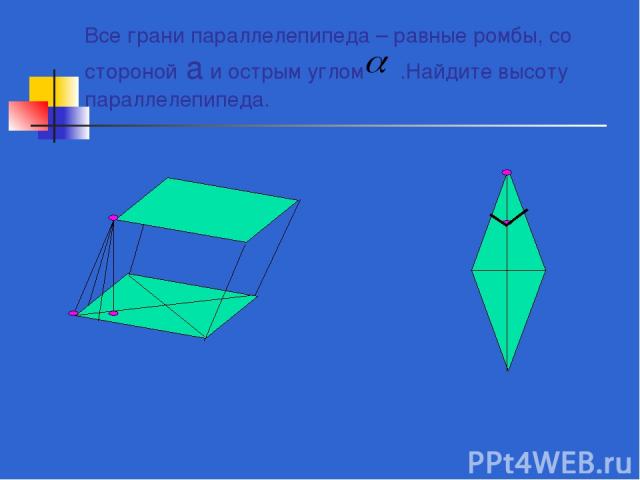
Все грани параллелепипеда – равные ромбы, со стороной а и острым углом .Найдите высоту параллелепипеда.

Ответ:

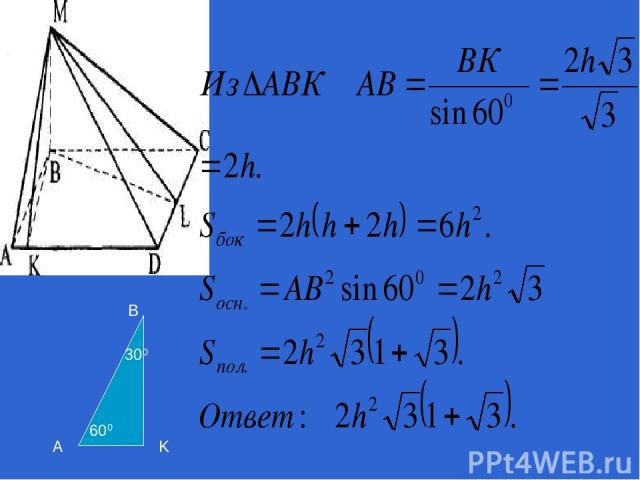
*Основанием пирамиды служит ромб. Две боковые грани перпендикулярны плоскости основания и двугранный угол, образуемый ими равен 120°; две другие грани наклонены к плоскости основания под углом в 30°. Высота пирамиды h. Найдите площадь полной поверхности пирамиды.

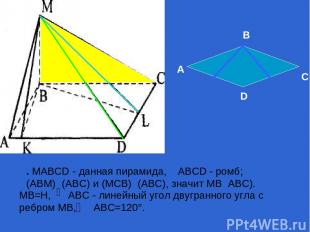
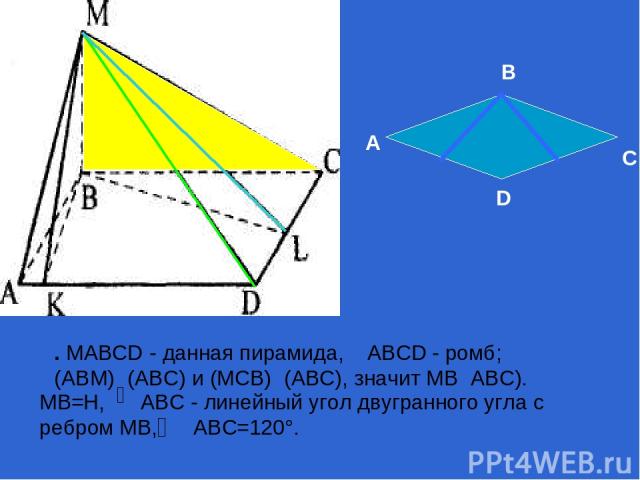
. MABCD - данная пирамида, ABCD - ромб; (ABM)┴(ABC) и (МСВ)┴(АВС), значит МВ┴АВС). MB=Н, ABC - линейный угол двугранного угла с ребром MB, ABC=120°. А В С D

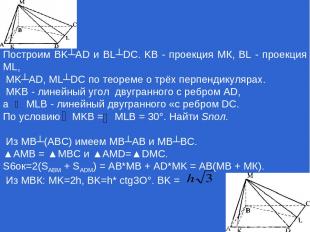
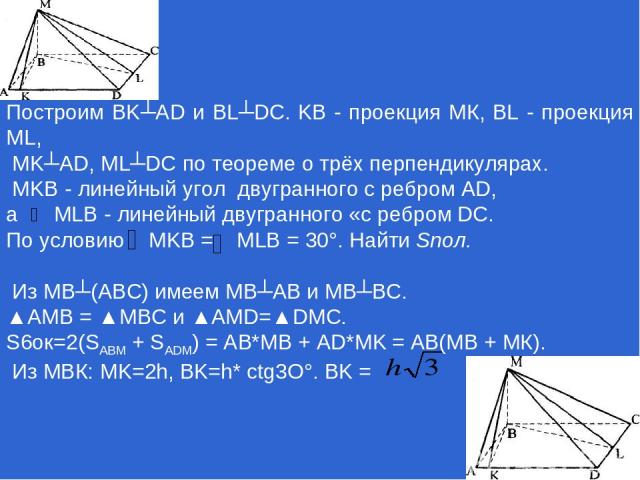
Построим BK┴AD и BL┴DC. KB - проекция МК, BL - проекция ML, MK┴AD, ML┴DC по теореме о трёх перпендикулярах. MKB - линейный угол двугранного с ребром AD, a MLB - линейный двугранного «с ребром DC. По условию MKB = MLB = 30°. Найти Snoл. Из MB┴(ABC) имеем МВ┴АВ и МВ┴ВС. ▲АМВ = ▲МВС и ▲AMD=▲DMC. S6oк=2(SАВМ + SADM) = АВ*МВ + AD*MK = АВ(МВ + МК). Из МВК: MK=2h, BK=h* ctg3O°. BK =

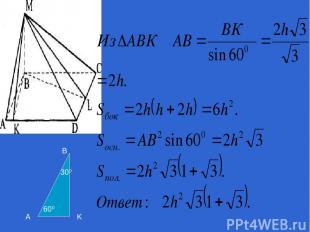
A B K 300 600

Подводим итог урока, определяем двугранные углы пирамид и призм, используем одну из презентаций, составленных учениками в домашней работе.

Презентация по геометрии. Тема: « Двугранный угол». Выполнила: Першина Анастасия Ученица 10 «а» класса 2008-2009 учебный год Усть-Качкинская СОШ. 2004©

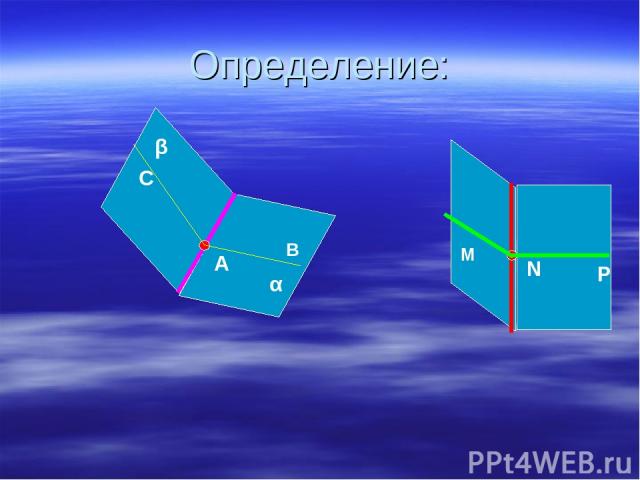
Любая прямая, проведенная в данной плоскости, разделяет эту плоскость на две полуплоскости. Перегнем плоскость по прямой а так, что две полуплоскости с границей а оказались уже не лежащими в одной плоскости. Полученная фигура и есть двугранный угол.

Определение: Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а , не принадлежащими одной плоскости.

Полуплоскости, образующие двугранный угол, называются его гранями. У двугранного угла две грани, отсюда и название – двугранный угол. Прямая а – общая граница полуплоскостей – называется ребром двугранного угла.

Отметим на ребре двугранного угла какую-нибудь точку и в каждой грани из этой точки проведем луч перпендикулярно к ребру. Образованный этими лучами угол называется линейным углом двугранного угла.

Градусная мера угла. Градусной мерой угла называется градусная мера его линейного угла.(a). Двугранный угол называется прямым (острым, тупым), если он равен 90º (меньше 90º, больше 90º).(б).

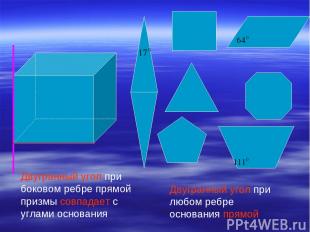
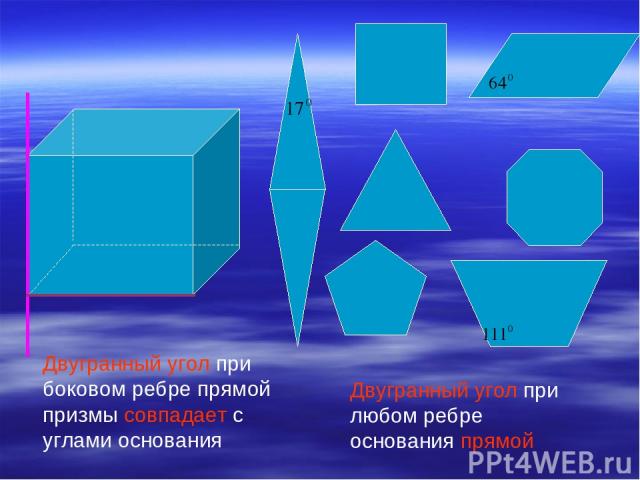
Двугранный угол при боковом ребре прямой призмы совпадает с углами основания Двугранный угол при любом ребре основания прямой

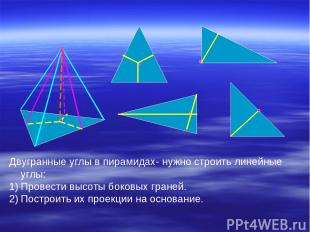
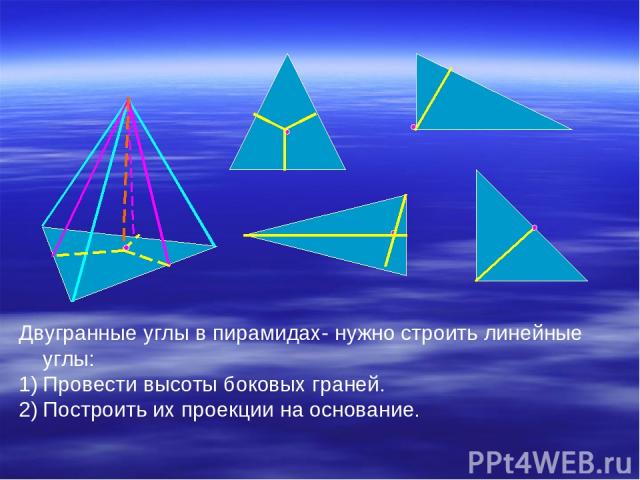
Двугранные углы в пирамидах- нужно строить линейные углы: Провести высоты боковых граней. Построить их проекции на основание.