Презентация на тему: Компланарные векторы

900igr.net

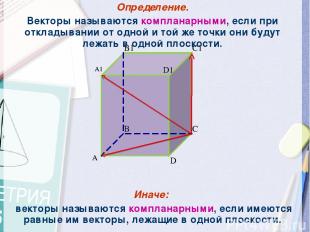
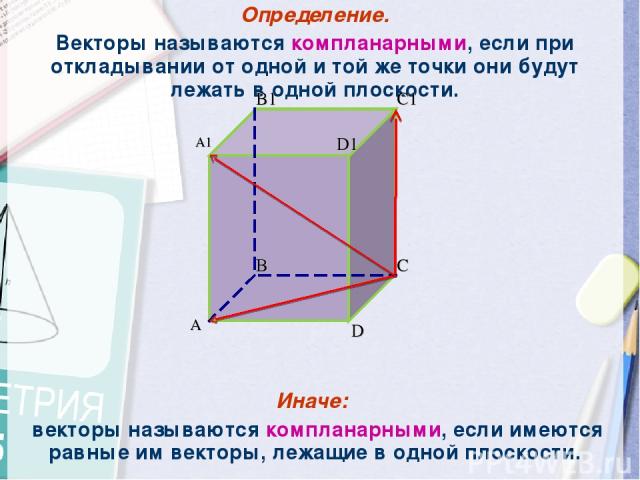
Определение. Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости. Иначе: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости. A B C D A1 B1 C1 D1

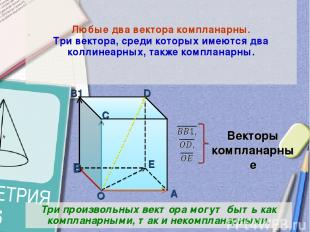
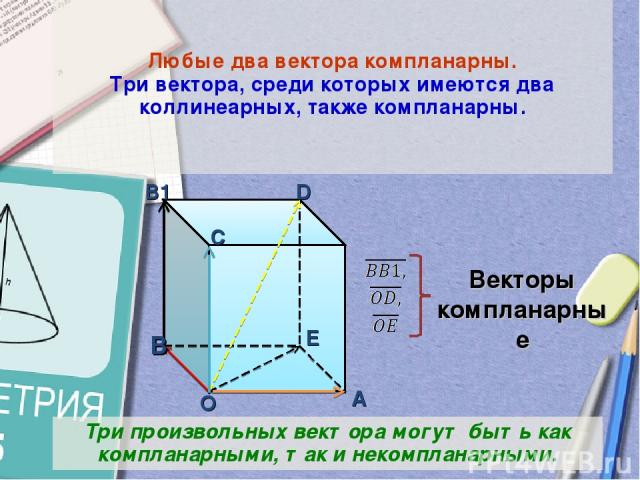
Любые два вектора компланарны. Три вектора, среди которых имеются два коллинеарных, также компланарны. B B1 O C D E A Векторы компланарные Три произвольных вектора могут быть как компланарными, так и некомпланарными.

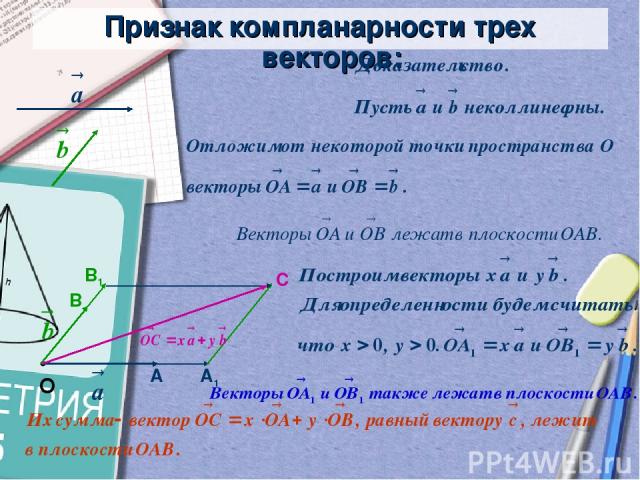
Признак компланарности трех векторов:

Признак компланарности трех векторов: • О А1 В1 С

Определение. Утверждение, обратное признаку компланарности векторов: Докажем это.

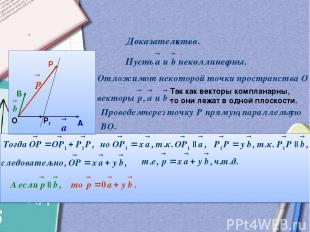
О А В Р Р1 Так как векторы компланарны, то они лежат в одной плоскости.

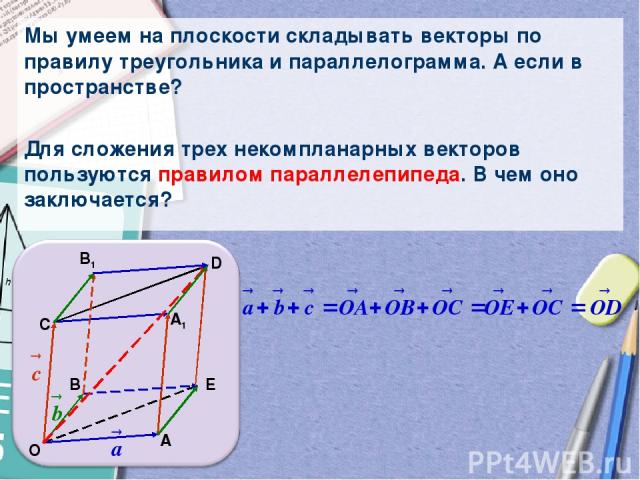
Мы умеем на плоскости складывать векторы по правилу треугольника и параллелограмма. А если в пространстве? Для сложения трех некомпланарных векторов пользуются правилом параллелепипеда. В чем оно заключается? Е С В А О D B1 A1