Презентация на тему: Компланарные векторы

Компланарные векторы

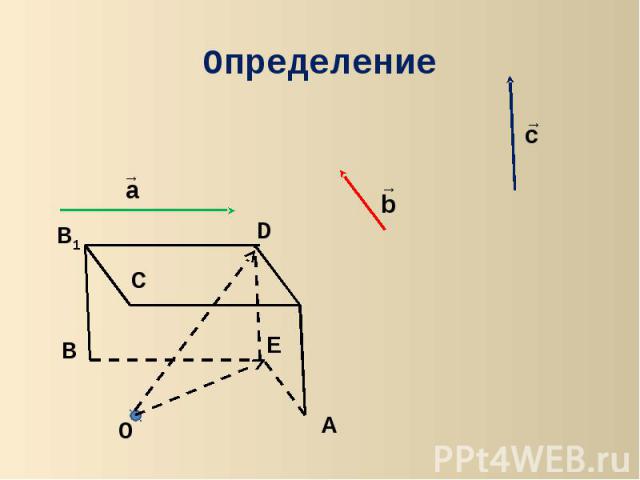
Определение Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

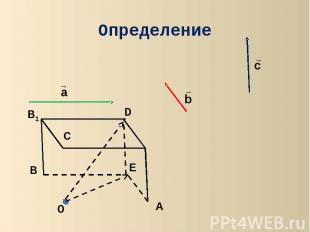
Определение

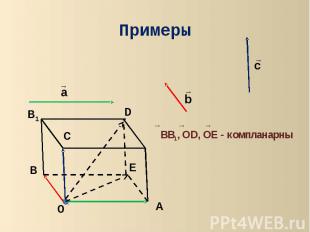
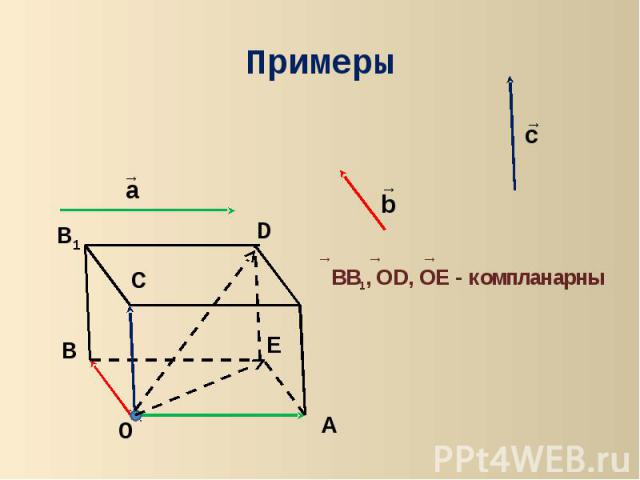
ПримерыBB1, OD, OE - компланарны

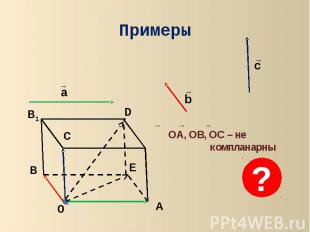
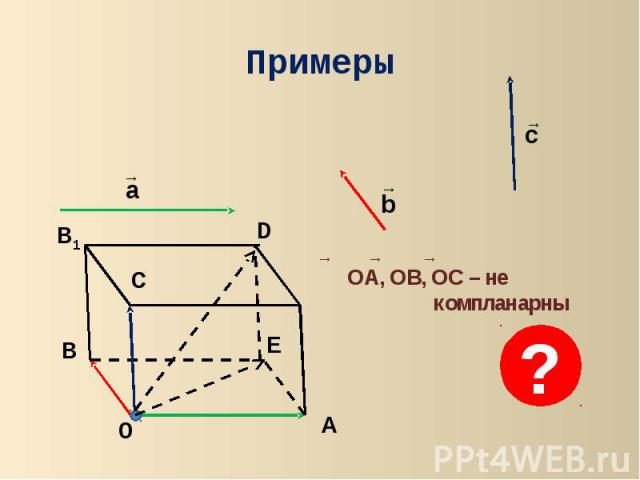
ПримерыOA, OB, OC – не компланарны

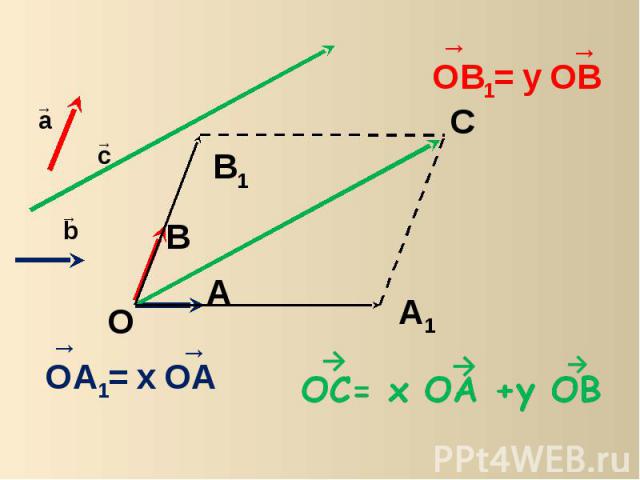
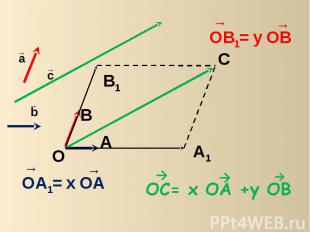
Если вектор с можно разложить по векторам a и b, т.е. представить в видес= x a + y b,где x , y – некоторые числа, то векторы a, b, c компланарны.

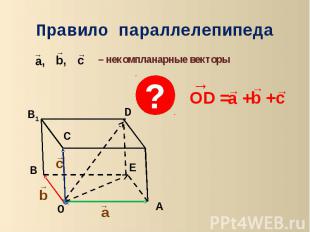
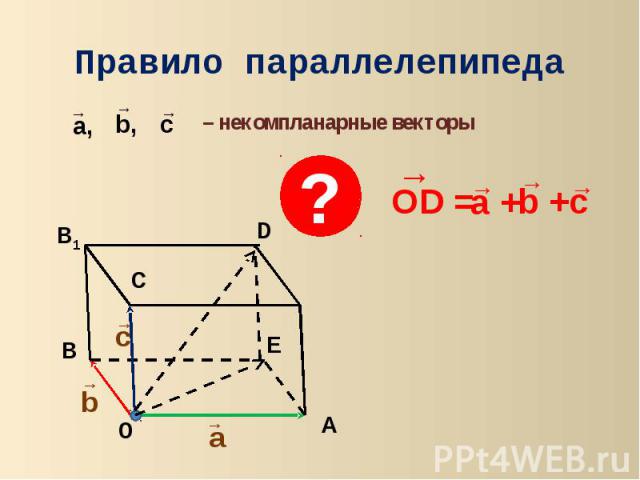
Правило параллелепипеда – некомпланарные векторы

Разложение вектора по трем некомпланарным векторамЕсли вектор p представлен в видеp= x a + y b + z c,где x , y , z – некоторые числа, то говорят , что вектор p разложен по векторам a, b, c.Числа x , y , z называются коэффициентами разложения.

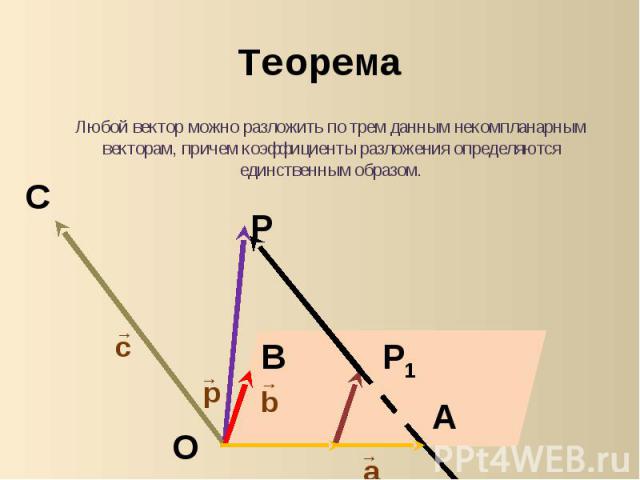
Теорема Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.

Теорема Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.

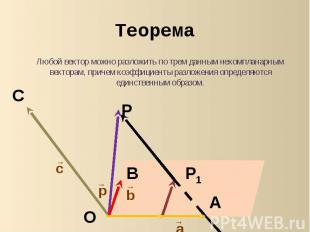
Теорема Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.