Презентация на тему: ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ

ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 126

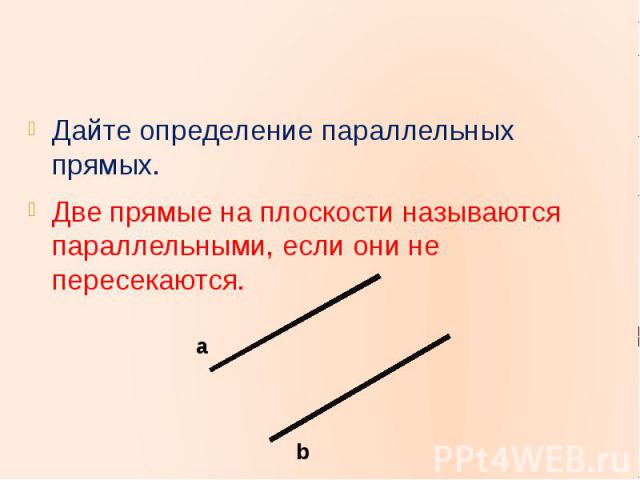
Дайте определение параллельных прямых.Дайте определение параллельных прямых.Две прямые на плоскости называются параллельными, если они не пересекаются.

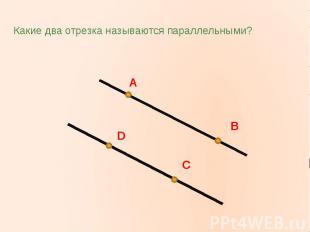
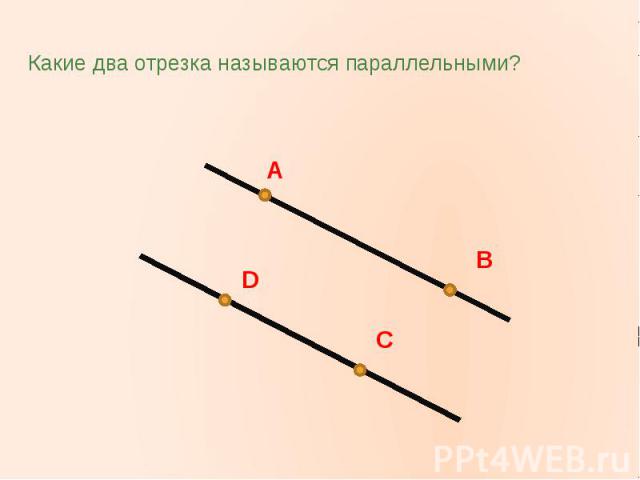
Какие два отрезка называются параллельными?

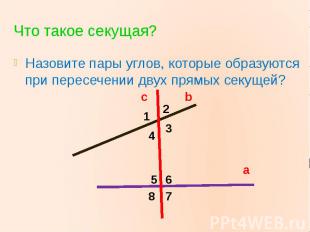
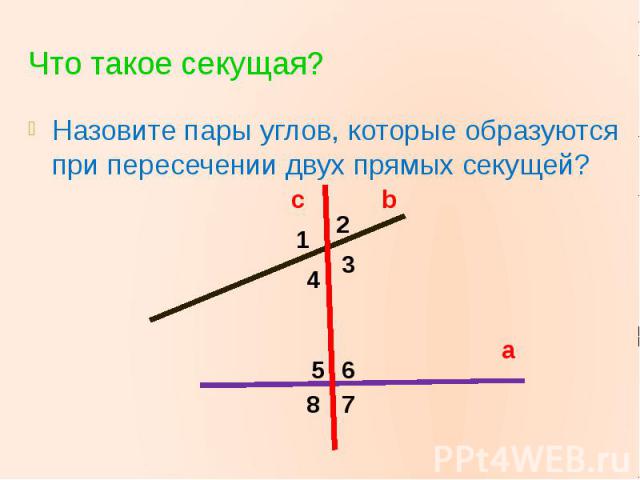
Что такое секущая?Назовите пары углов, которые образуются при пересечении двух прямых секущей?

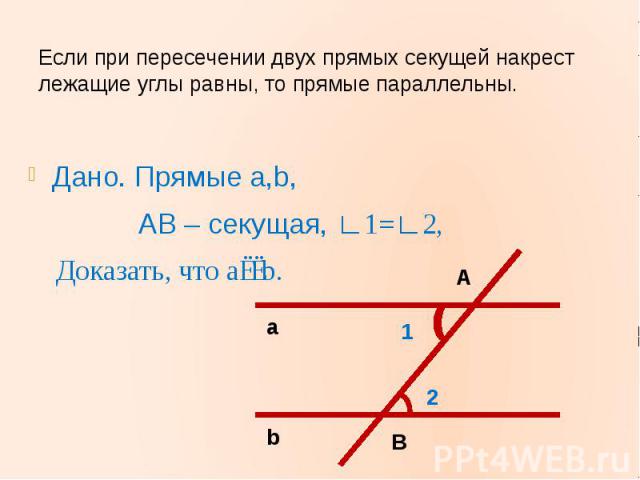
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.Дано. Прямые a,b, AB – секущая, ∟1=∟2, Доказать, что a∣∣b.

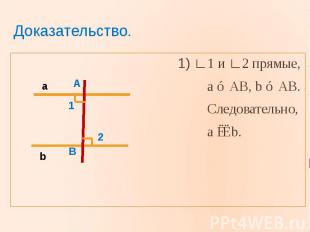
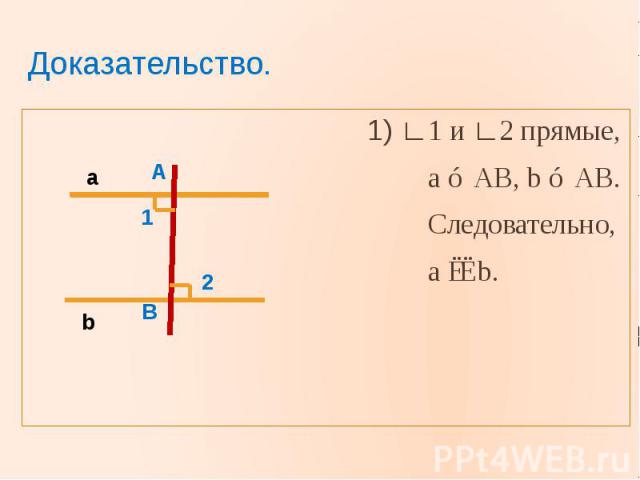
Доказательство. 1) ∟1 и ∟2 прямые, a ⊥ AB, b ⊥ AB. Следовательно, a ∣∣ b.

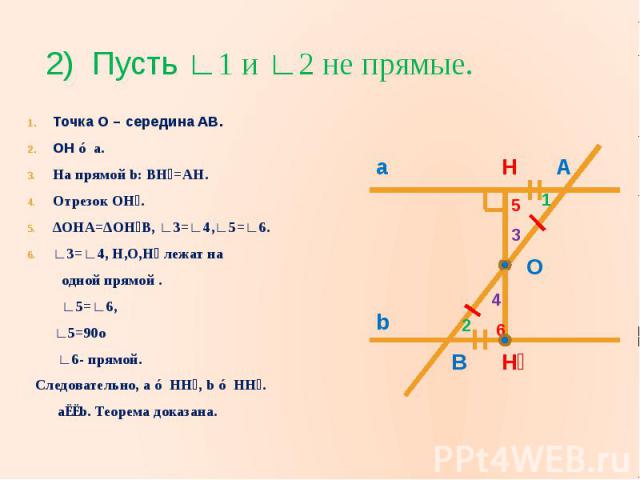
2) Пусть ∟1 и ∟2 не прямые.Точка О – середина AB.OH ⊥ a.На прямой b: BH₁=AH.Отрезок OH₁.∆OHA=∆OH₁B, ∟3=∟4,∟5=∟6.∟3=∟4, H,O,H₁ лежат на одной прямой . ∟5=∟6, ∟5=90о ∟6- прямой. Следовательно, a ⊥ HH₁, b ⊥ HH₁. a∣∣b. Теорема доказана.

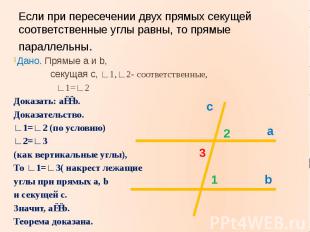
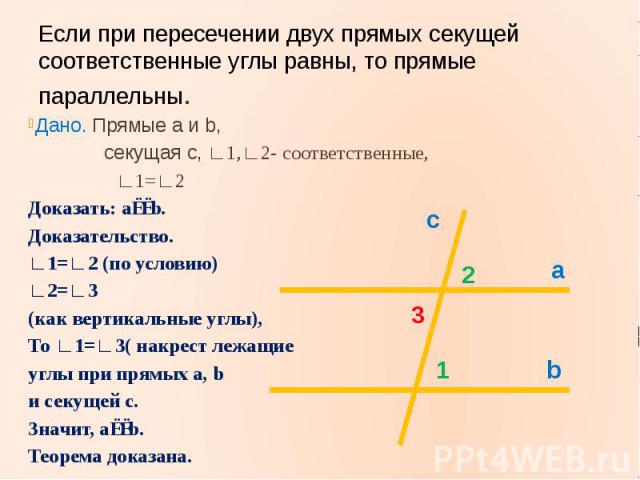
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.Дано. Прямые a и b, секущая c, ∟1,∟2- соответственные, ∟1=∟2Доказать: a∣∣b.Доказательство.∟1=∟2 (по условию)∟2=∟3 (как вертикальные углы),То ∟1=∟3( накрест лежащиеуглы при прямых а, bи секущей с.Значит, a∣∣b.Теорема доказана.

Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰, то прямые параллельны.Дано. прямые a и b, секущая c, ∟1+∟4=180⁰ Доказать: a∣∣b.Доказательство.∟1+∟4=180⁰ (по условию),∟3 + ∟4 =180⁰, значит, ∟3 = ∟1(накрест лежащие углы), значит a ∣∣ b. Теорема доказана.

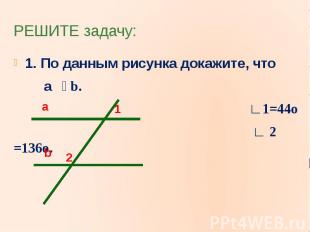
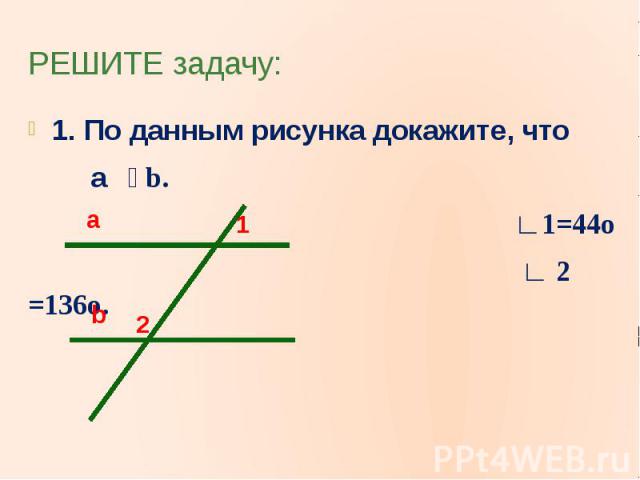
РЕШИТЕ задачу:1. По данным рисунка докажите, что a b. ∟1=44o ∟ 2 =136o.

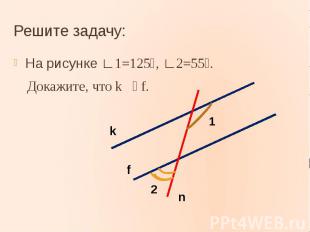
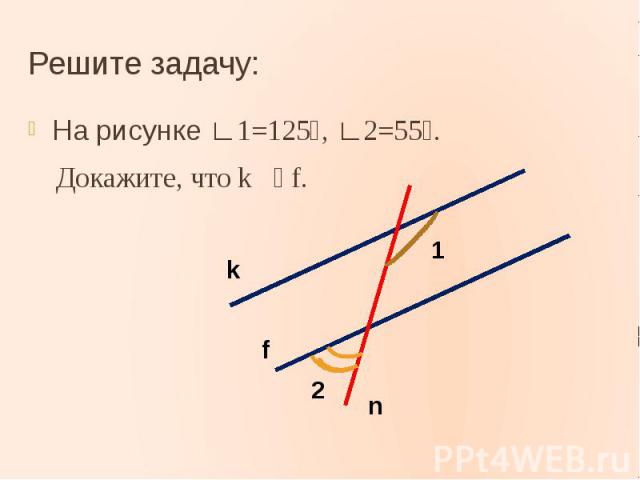
Решите задачу:На рисунке ∟1=125⁰, ∟2=55⁰. Докажите, что k f.

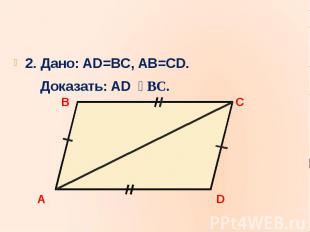
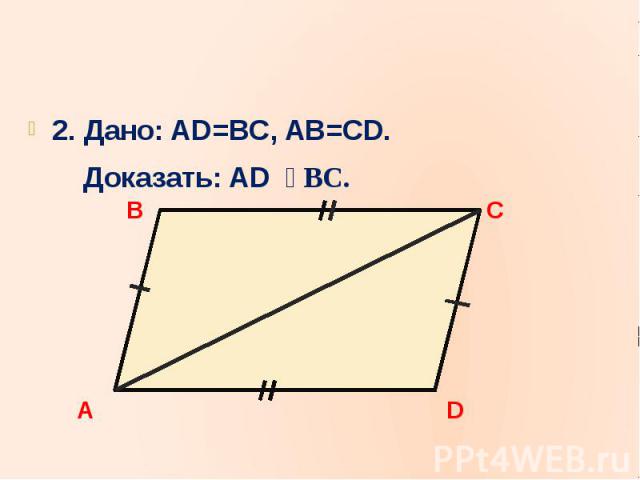
2. Дано: AD=BC, AB=CD.2. Дано: AD=BC, AB=CD. Доказать: AD BC.

В классе№ 186(в), № 189.

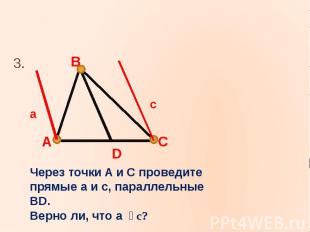
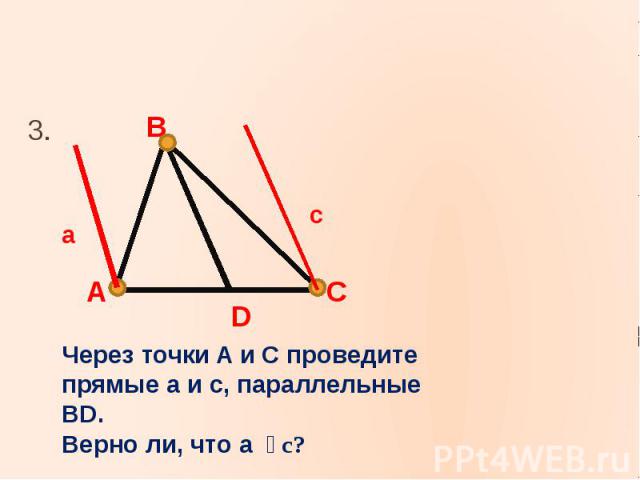
3.3.

Домашнее задание повторить теорию: п.25-п.26, №187, №189, №186(а,б)