Презентация на тему: Параллельность прямой и плоскости. Решение задач

Урок 7 (8) Параллельность прямой и плоскости. Решение задач
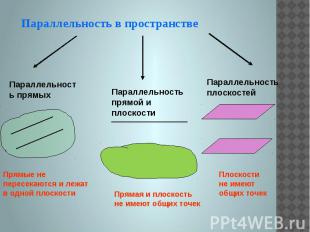
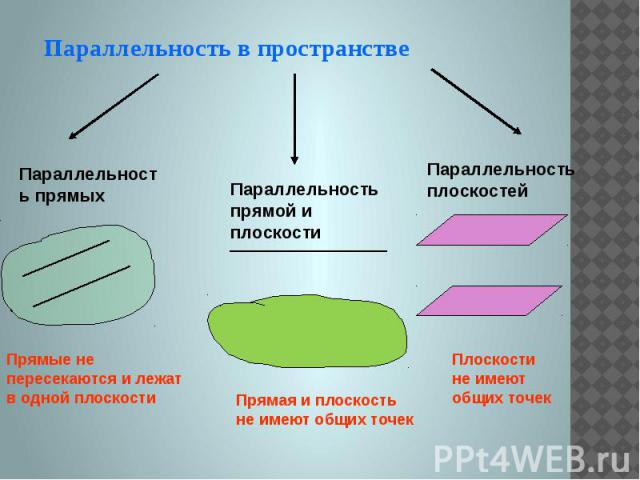
Параллельность в пространстве

Теорема: Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. Дано: а, , ab а, b Доказать: аДоказательство:По условию ab, bПусть а(по Лемме) b -W b а=(по определению) а

Следствие 1: Если плоскость проходит через данную прямую , параллельную другой плоскости и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой Дано: а, , , а, а, Доказать: аb

Следствие 2: Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости Дано: ab; aДоказать: 1) b; 2)b

Решение задач с комментариями №18 (б)№20№22№26

Домашнее задание П.6 №18 (а), 19, 21, 24, 28