Презентация на тему: Компланарные векторы. Правило параллелепипеда

Тема урока:Компланарные векторы. Правило параллелепипеда.

Цели урока: - усвоить определение компланарных векторов;- рассмотреть признак компланарности трёх векторов;- рассмотреть правило параллелепипеда сложения трёх некомпланарных векторов;- научиться применять полученные знания при решении задач.

Определение Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости.Иначе: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

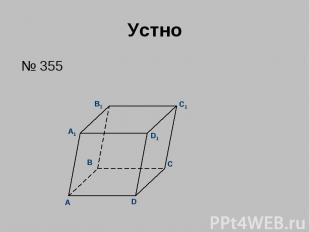
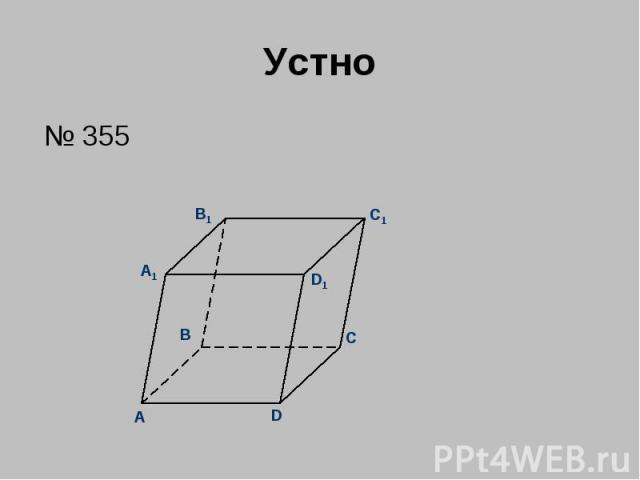
Устно № 355

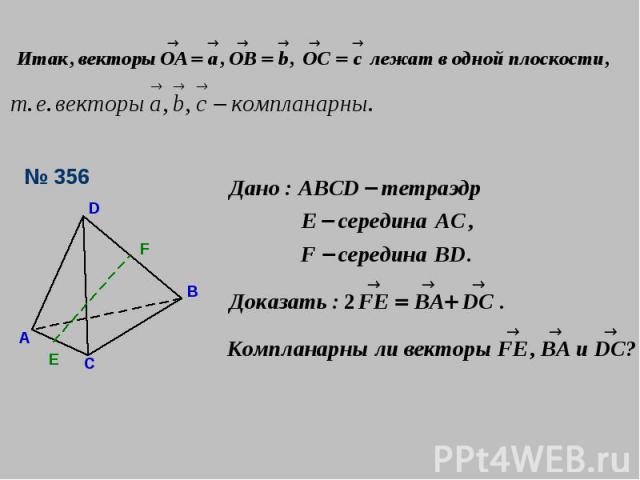
Признак компланарности трёх векторов

Правило параллелепипеда Для сложения трех некомпланарных векторов можно пользоваться так называемым правилом параллелепипеда.

Домашнее задание:п.39, 40№ 358

Тема урока: Разложение вектора по трем некомпланарным векторам.

Цели урока - изучить теорему о разложении вектора по трём некомпланарным векторам;- научиться применять полученные знания при решении задач.

ОПРЕДЕЛЕНИЕ Если вектор представлен в виде:где x, y, z – некоторые числа, то говорят, что вектор разложен по векторам , и .Числа x, y, z называются коэффициентами разложения.

Теорема. Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.

Векторы коллинеарны, поэтому существуют числа х, у, z такие, что .

В классе: № 360 (а)Домашнее задание:п.41 № 360 (б), № 368