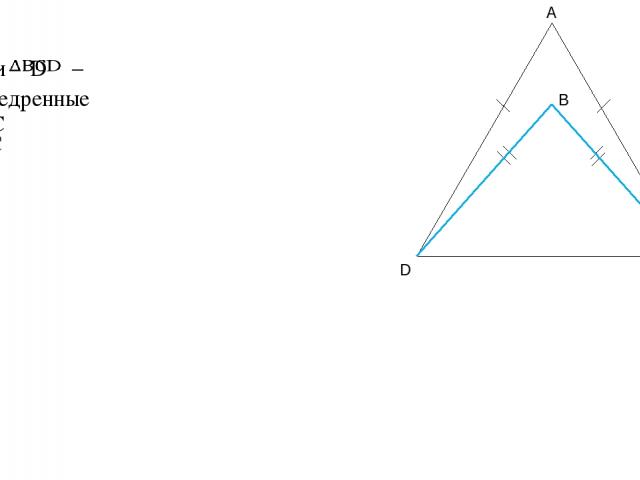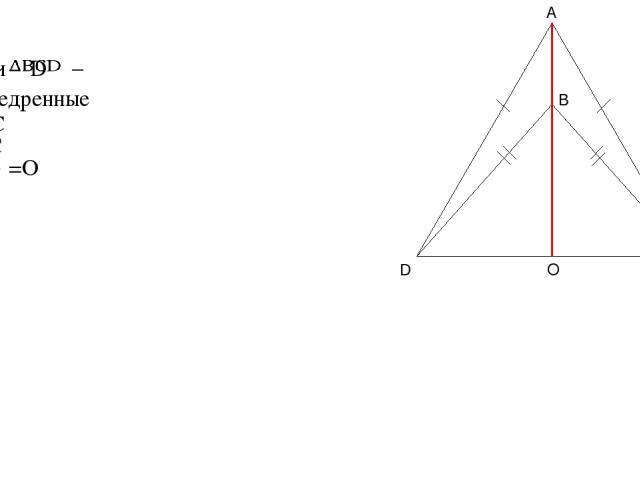Презентация на тему: Геометрия 7 класс

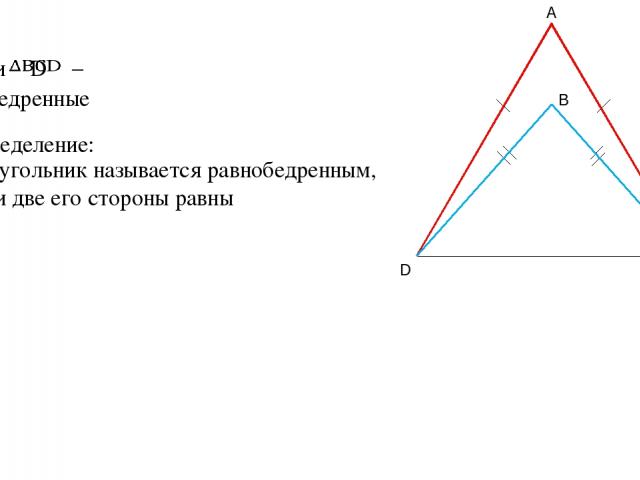
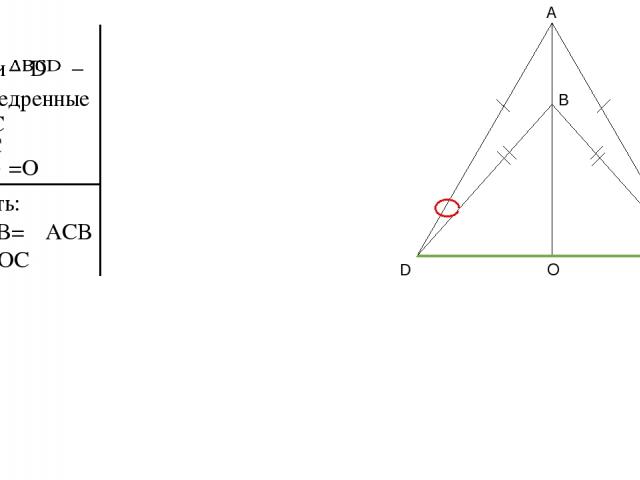
№ 142 Лутовинов А.И. ГЕОМЕТРИЯ 7 класс АтанАсян Л.С. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая AB пересекает отрезок CD в точке О. Докажите, что: а) ADB=ACB; б) DO=OC.

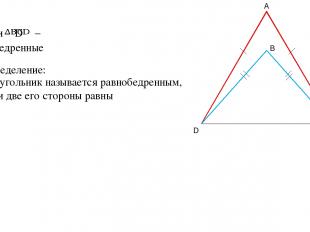
Дано: – и равнобедренные Определение: Треугольник называется равнобедренным, если две его стороны равны A D C B

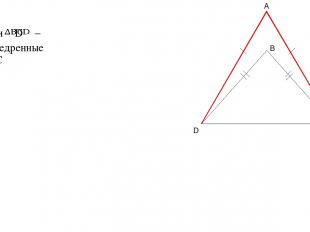
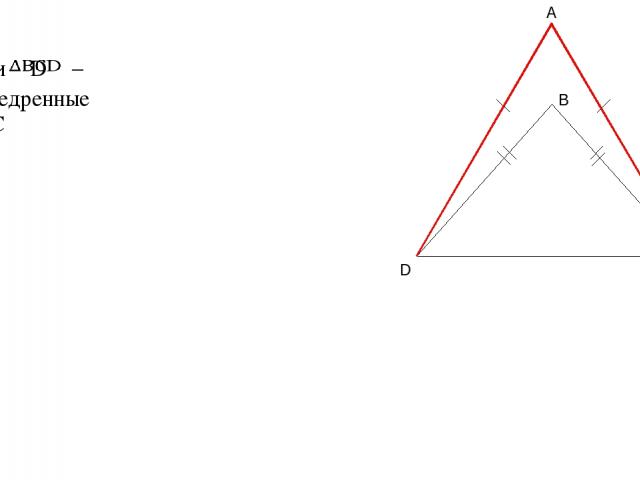
Дано: – и равнобедренные AD=AC A D C B

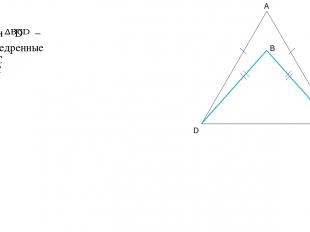
Дано: – и равнобедренные AD=AC BD=BC A D C B

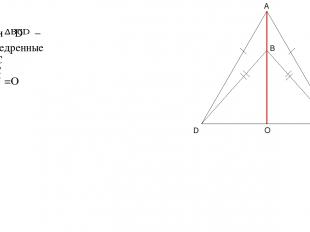
Дано: – и равнобедренные AD=AC BD=BC O =O A D C B

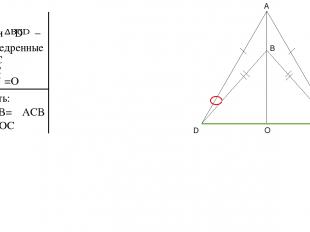
Дано: – и равнобедренные AD=AC BD=BC O =O Доказать: а)∠ADB=∠ACB б) DO=OC A D C B

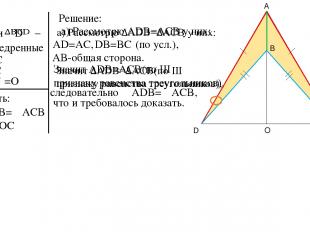
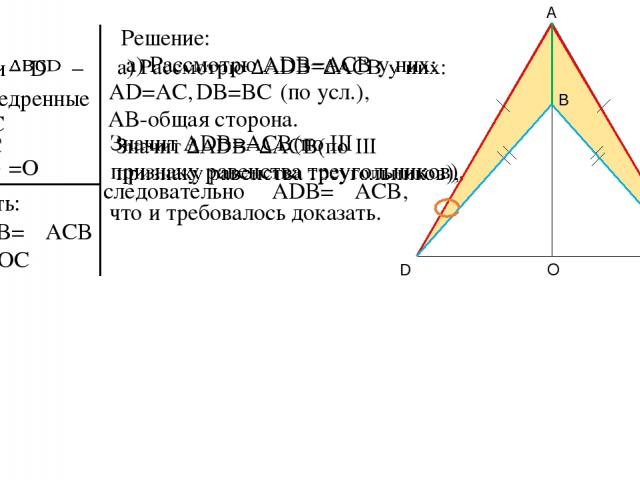
Дано: – и равнобедренные AD=AC BD=BC O =O Доказать: б) DO=OC Решение: а)∠ADB=∠ACB AD=AC, DB=BC AB-общая сторона. следовательно ∠ADB=∠ACB, что и требовалось доказать. (по усл.), A D C B

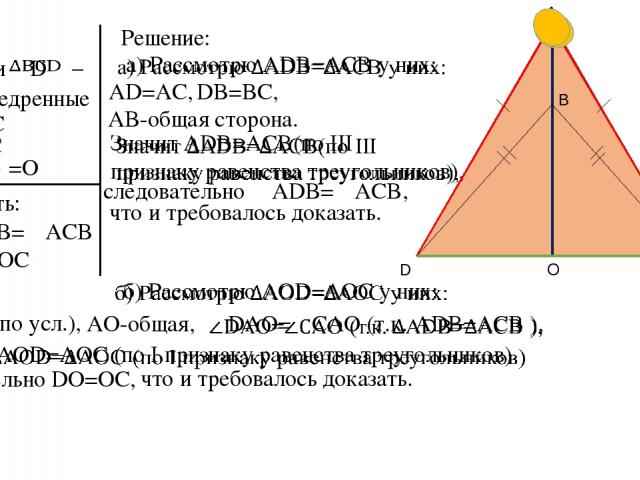
Дано: – и равнобедренные AD=AC BD=BC O =O Доказать: б) DO=OC Решение: а)∠ADB=∠ACB AD=AC, DB=BC, AB-общая сторона. следовательно ∠ADB=∠ACB, что и требовалось доказать. AD=AC (по усл.), AO-общая, следовательно DO=OC, что и требовалось доказать. A D C B

Дано: – и равнобедренные AD=AC BD=BC O =O Доказать: б) DO=OC Решение: а)∠ADB=∠ACB AD=AC, DB=BC, AB-общая сторона. следовательно ∠ADB=∠ACB, что и требовалось доказать. AD=AC (по усл.), AO-общая, следовательно DO=OC, что и требовалось доказать. A D C B