Презентация на тему: Объём геометрических фигур

ОБЪЕМ ФИГУР В ПРОСТРАНСТВЕ Объем – величина, аналогичная площади и сопоставляющая фигурам в пространстве неотрицательные действительные числа. Для объемов пространственных фигур справедливы свойства, аналогичные свойствам площадей плоских фигур, а именно: 1. Равные фигуры имеют равные объемы. 2. Если фигура Ф составлена из двух неперекрывающихся фигур Ф1 и Ф2, то объем фигуры Ф равен сумме объемов фигур Ф1 и Ф2, т.е. V(Ф)=V(Ф1)+V(Ф2). 3. Объем прямоугольного параллелепипеда равен произведению трех его измерений, т. е. имеет место формула где a, b, c – ребра параллелепипеда. Две фигуры, имеющие равные объемы, называются равновеликими. 900igr.net

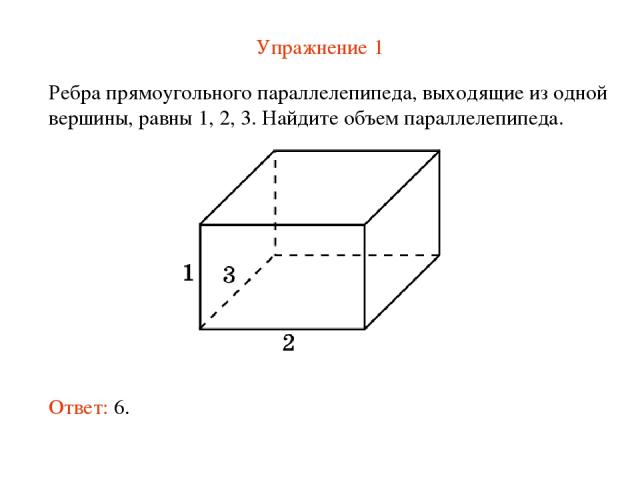
Упражнение 1 Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите объем параллелепипеда. Ответ: 6.

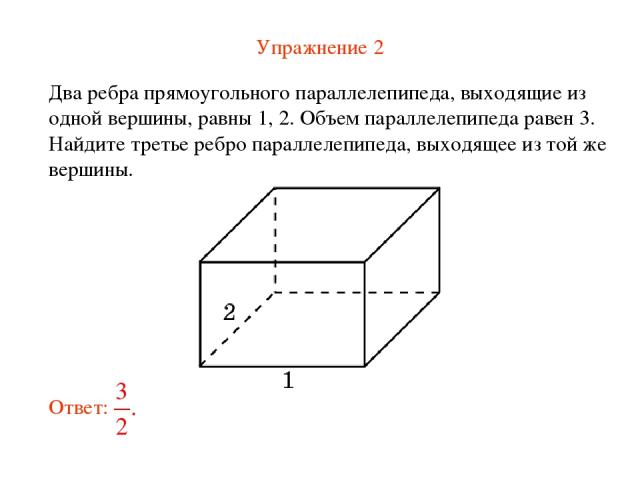
Упражнение 2 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 3. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

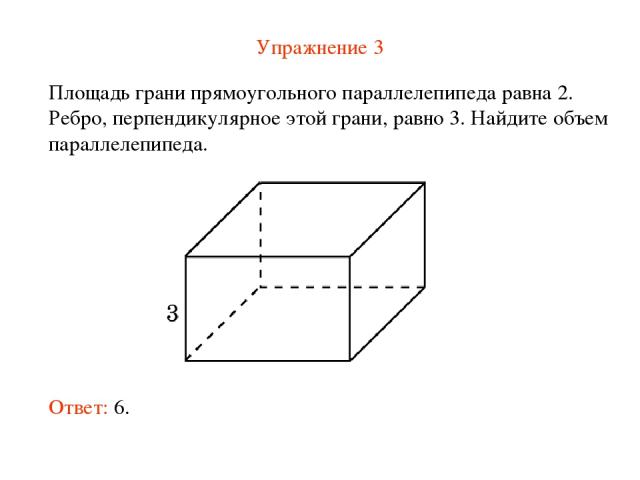
Упражнение 3 Площадь грани прямоугольного параллелепипеда равна 2. Ребро, перпендикулярное этой грани, равно 3. Найдите объем параллелепипеда. Ответ: 6.

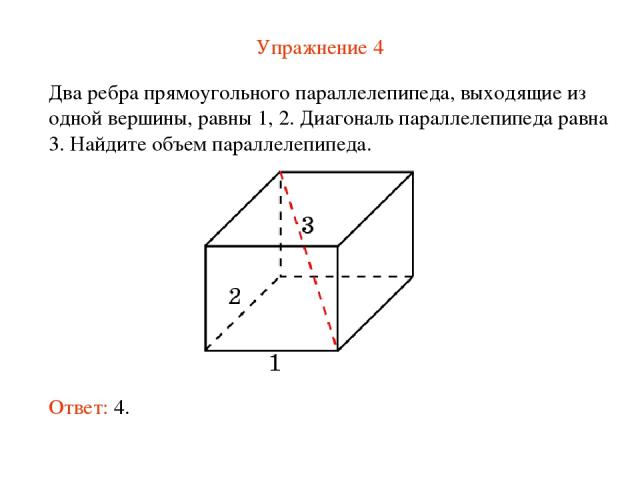
Упражнение 4 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Диагональ параллелепипеда равна 3. Найдите объем параллелепипеда. Ответ: 4.

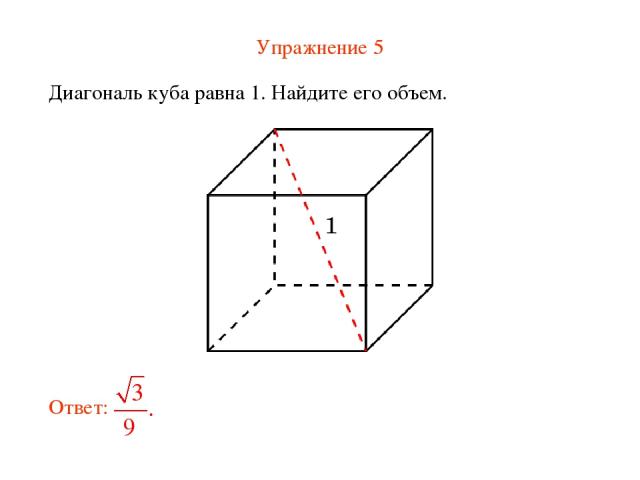
Упражнение 5 Диагональ куба равна 1. Найдите его объем.

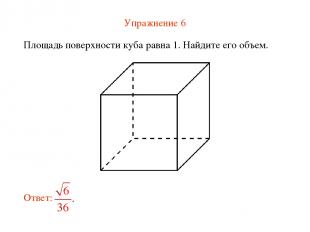
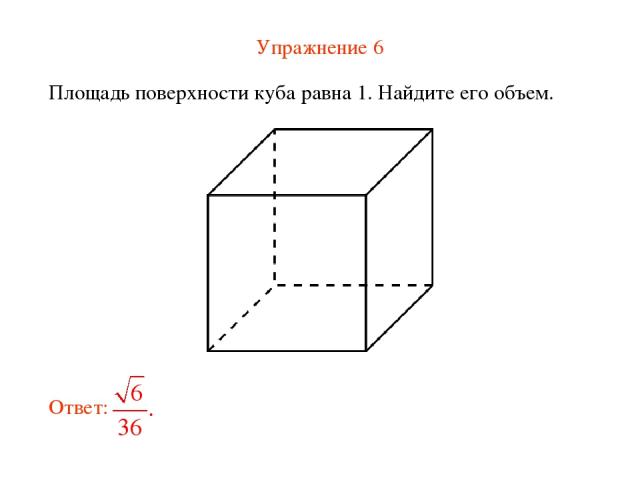
Упражнение 6 Площадь поверхности куба равна 1. Найдите его объем.

Упражнение 7 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 10. Найдите объем параллелепипеда.

Упражнение 8 Ребро прямоугольного параллелепипеда равно 1. Диагональ равна 3. Площадь поверхности параллелепипеда равна 16. Найдите объем параллелепипеда.

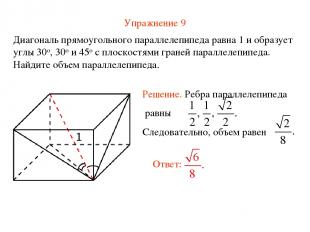
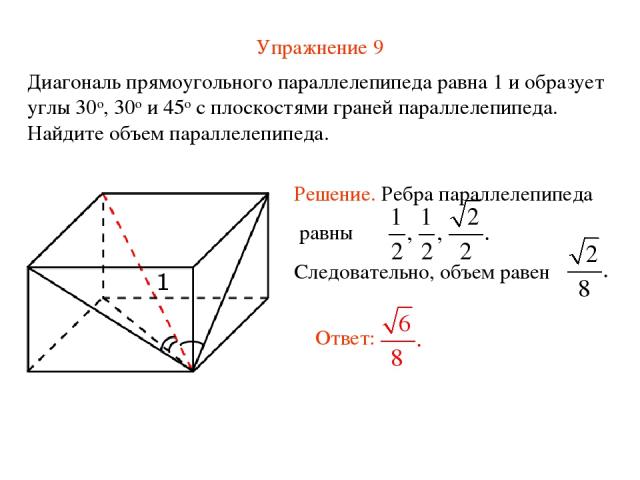
Упражнение 9 Диагональ прямоугольного параллелепипеда равна 1 и образует углы 30о, 30о и 45о с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

Упражнение 10 Площади трех граней параллелепипеда равны 1, 2, 3. Найдите объем параллелепипеда.

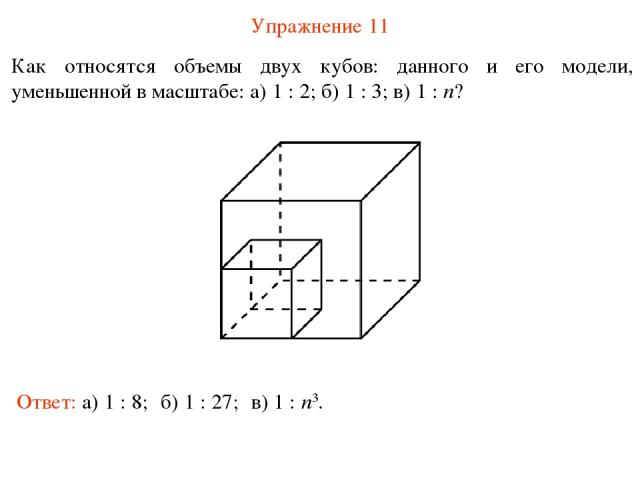
Упражнение 11 Как относятся объемы двух кубов: данного и его модели, уменьшенной в масштабе: а) 1 : 2; б) 1 : 3; в) 1 : n? Ответ: а) 1 : 8; б) 1 : 27; в) 1 : n3.

Упражнение 12 Как изменится объем прямого параллелепипеда, если: а) одно из его измерений увеличить в 2 раза, в 3 раза, в n раз; б) если два его измерения увеличить, причем каждое из них в 2, 3, n раз; в) если все три его измерения увеличить в 2, 3, n раз? Ответ: а) Увеличится в 2 раза, в 3 раза, в n раз; б) увеличится в 4 раза, в 9 раза, в n2 раз; в) увеличится в 8 раз, в 27 раз, в n3 раз.

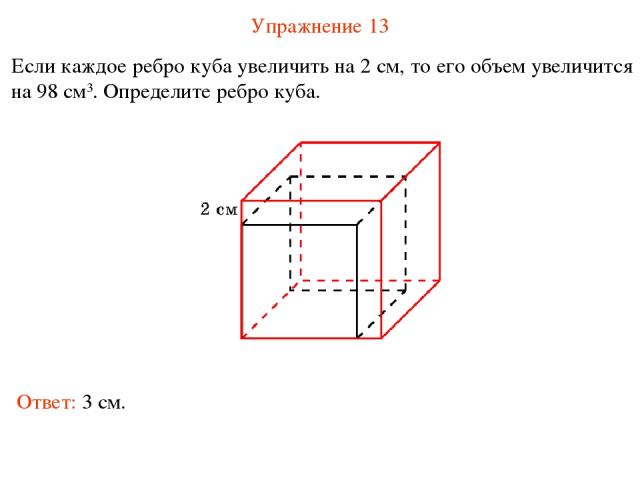
Упражнение 13 Если каждое ребро куба увеличить на 2 см, то его объем увеличится на 98 см3. Определите ребро куба. Ответ: 3 см.

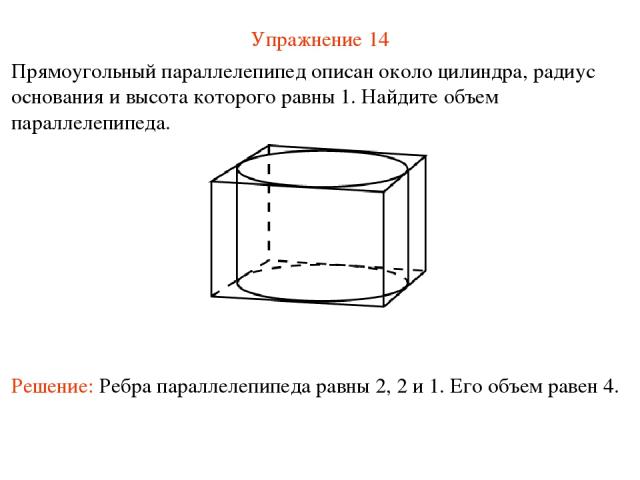
Упражнение 14 Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда. Решение: Ребра параллелепипеда равны 2, 2 и 1. Его объем равен 4.

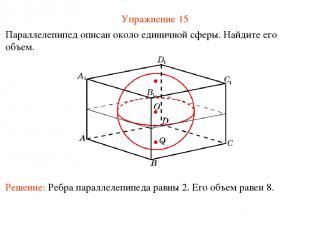
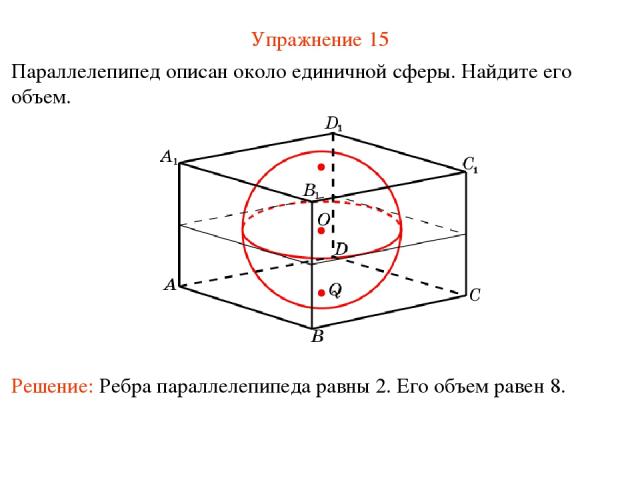
Упражнение 15 Параллелепипед описан около единичной сферы. Найдите его объем.

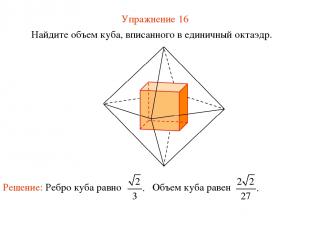
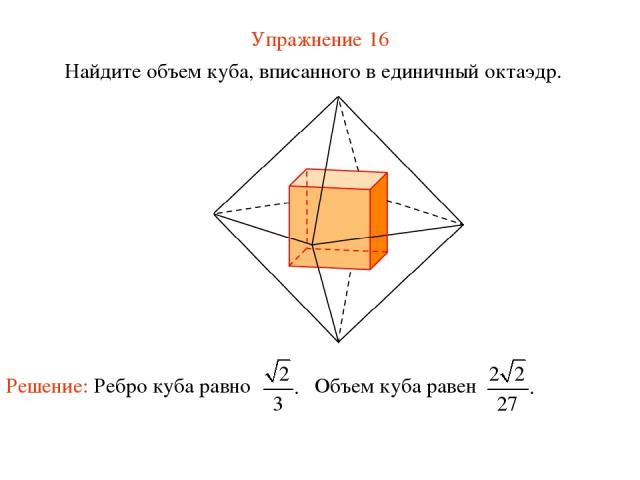
Упражнение 16 Найдите объем куба, вписанного в единичный октаэдр.

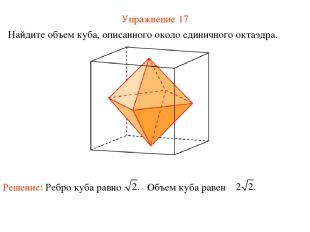
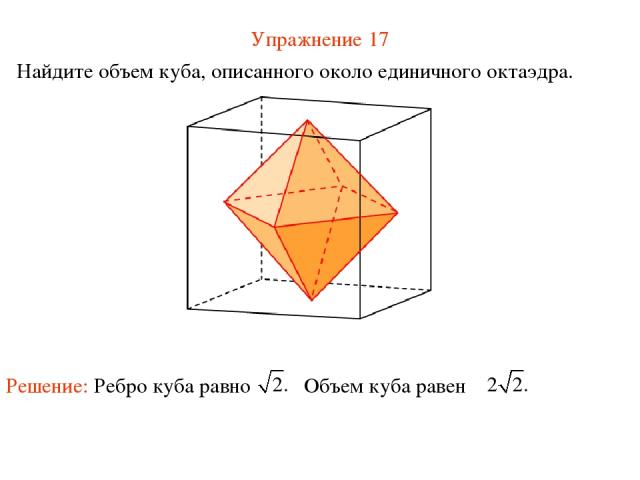
Упражнение 17 Найдите объем куба, описанного около единичного октаэдра.

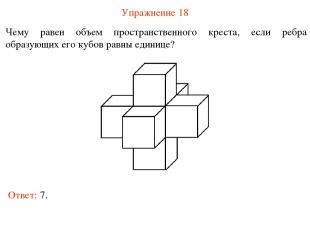
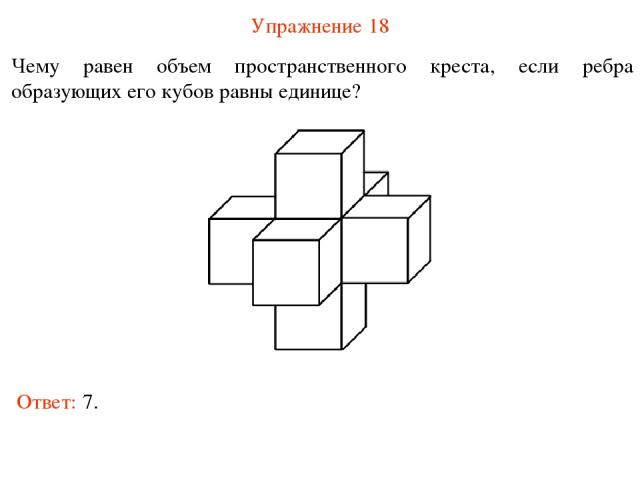
Упражнение 18 Чему равен объем пространственного креста, если ребра образующих его кубов равны единице? Ответ: 7.

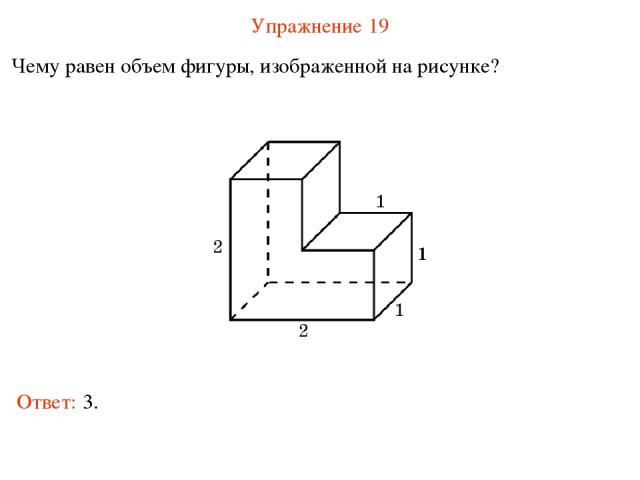
Упражнение 19 Чему равен объем фигуры, изображенной на рисунке? Ответ: 3.

Упражнение 20 Найдите объем детали, изображенной на рисунке (все углы – прямые). Ответ: 12 см3.

Упражнение 21 Найдите объем детали, изображенной на рисунке (все углы – прямые). Ответ: 40 см3.

Упражнение 22 Найдите объем детали, изображенной на рисунке (все углы – прямые). Ответ: 12 см3.

Упражнение 23 Найдите объем детали, изображенной на рисунке (все углы – прямые). Ответ: 10 см3.

Упражнение 24 Найдите объем детали, изображенной на рисунке (все углы – прямые). Ответ: 10 см3.

Упражнение 25 Найдите объем детали, изображенной на рисунке (все углы – прямые). Ответ: 5 см3.

Упражнение 26 Найдите объем детали, изображенной на рисунке (все углы – прямые). Ответ: 6 см3.

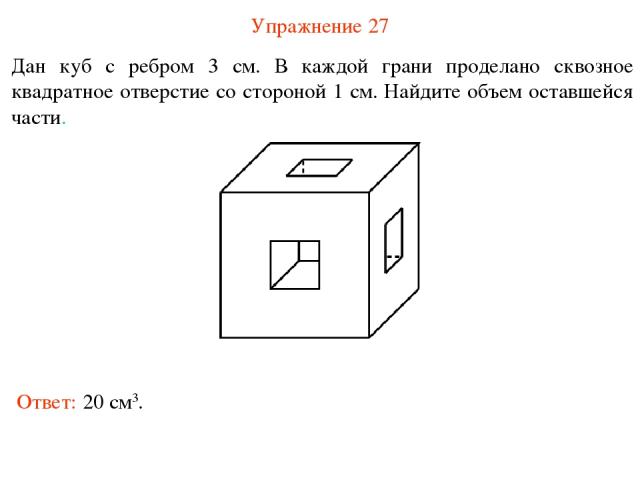
Упражнение 27 Дан куб с ребром 3 см. В каждой грани проделано сквозное квадратное отверстие со стороной 1 см. Найдите объем оставшейся части. Ответ: 20 см3.

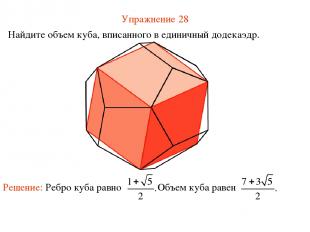
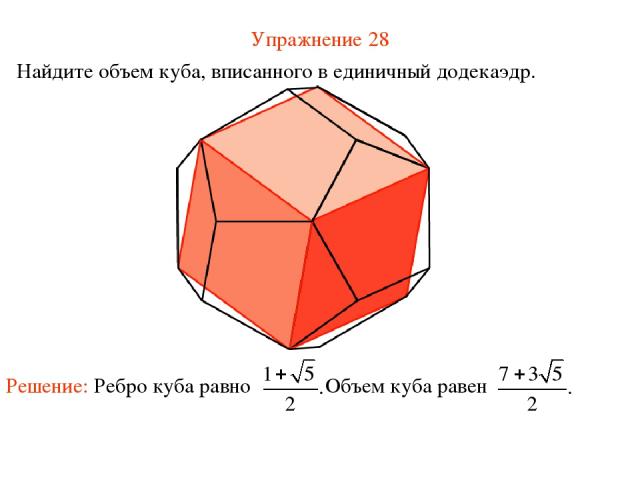
Упражнение 28 Найдите объем куба, вписанного в единичный додекаэдр.

Упражнение 29* Какой наибольший объем может иметь прямоугольный параллелепипед, сумма длин ребер которого, выходящих из одной вершины, равна 1?

Упражнение 30* Какую наименьшую площадь поверхности может иметь прямоугольный параллелепипед, объем которого равен 1?