Презентация на тему: Объёмы

Б. Кавальери Бонавентуре Кавальери (1598 – 1647) принадлежат труды по тригонометрии, логарифмам, геометрической оптике и т.д., но главным делом его жизни была книга «Геометрия, развитая новым способом при помощи неделимых непрерывного», в которой он предложил способ вычисления площадей плоских фигур и объемов пространственных тел, основанный на сравнении их сечений. Метод вычисления объемов пространственных тел, предложенный Б. Кавальери, называется принципом Кавальери. 900igr.net

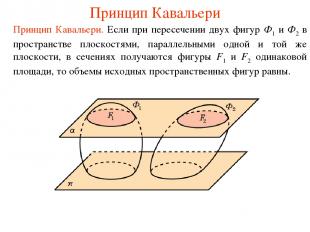
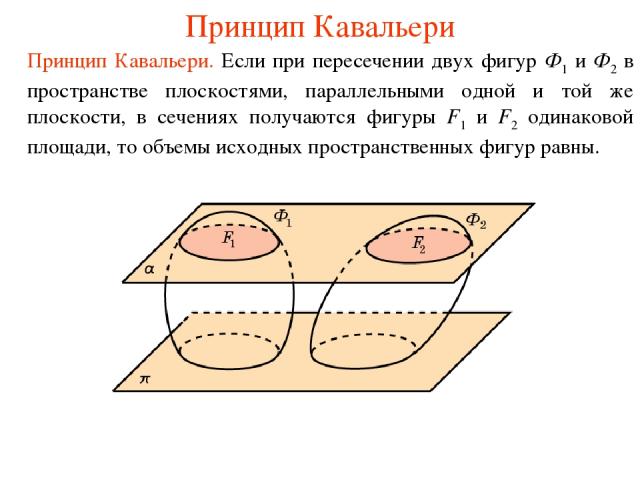
Принцип Кавальери Принцип Кавальери. Если при пересечении двух фигур Ф1 и Ф2 в пространстве плоскостями, параллельными одной и той же плоскости, в сечениях получаются фигуры F1 и F2 одинаковой площади, то объемы исходных пространственных фигур равны.

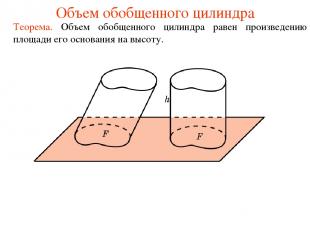
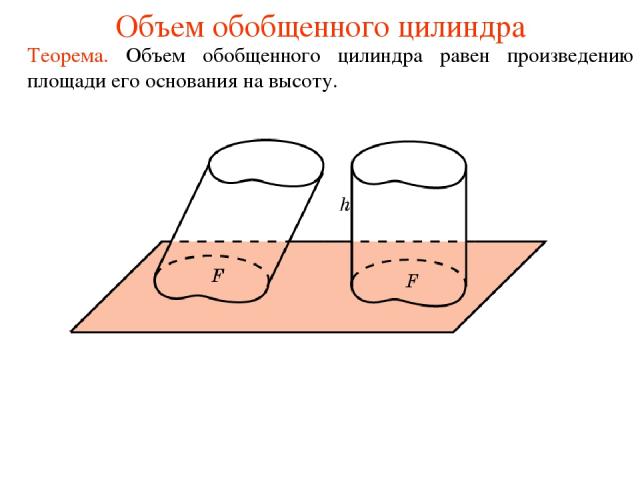
Объем обобщенного цилиндра Теорема. Объем обобщенного цилиндра равен произведению площади его основания на высоту.

Объем наклонного параллелепипеда 1 Объем наклонного параллелепипеда равен произведению площади S грани параллелепипеда на высоту h, проведенную к этой грани, т.е. имеет место формула

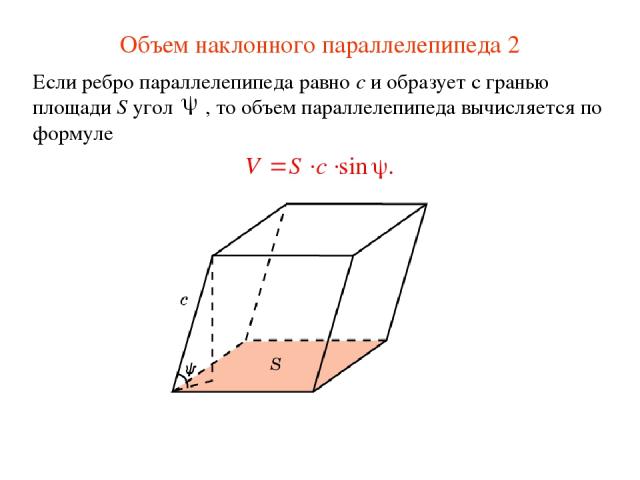
Объем наклонного параллелепипеда 2 Если ребро параллелепипеда равно c и образует с гранью площади S угол , то объем параллелепипеда вычисляется по формуле

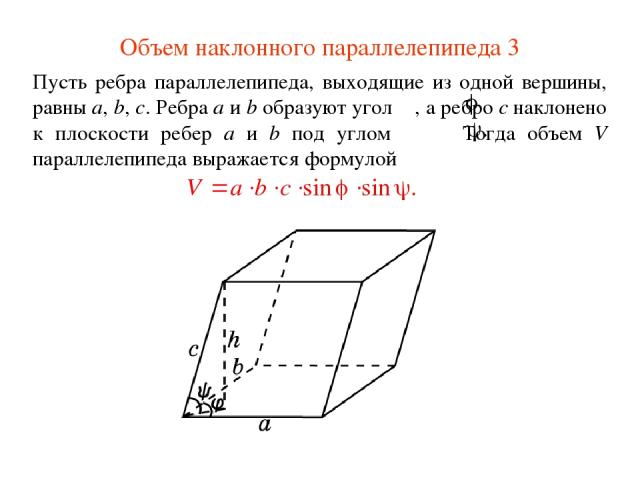
Объем наклонного параллелепипеда 3 Пусть ребра параллелепипеда, выходящие из одной вершины, равны a, b, c. Ребра a и b образуют угол , а ребро c наклонено к плоскости ребер a и b под углом Тогда объем V параллелепипеда выражается формулой

Упражнение 1 Две противоположные грани параллелепипеда – квадраты со стороной 1. Соединяющее их ребро равно 1 и наклонено к плоскостям этих граней под углом 60о. Найдите объем параллелепипеда.

Упражнение 2 Гранью параллелепипеда является ромб со стороной 1 и острым углом 60о. Одно из ребер параллелепипеда составляет с этой гранью угол 60о и равно 1. Найдите объем параллелепипеда.

Упражнение 3 Три грани параллелепипеда, имеющие общую вершину, являются ромбами со сторонами 1 и острыми углами при этой вершине 60о. Найдите объем параллелепипеда.

Упражнение 4 В параллелепипеде две грани имеют площади S1 и S2, их общее ребро равно a, и они образуют между собой двугранный угол 150о. Найдите объем параллелепипеда.

Упражнение 5 В параллелепипеде две грани являются прямоугольниками с площадями 20 см2 и 24 см2. Угол между их плоскостями равен 30о. Еще одна грань этого параллелепипеда имеет площадь 15 см2. Найдите объем параллелепипеда.

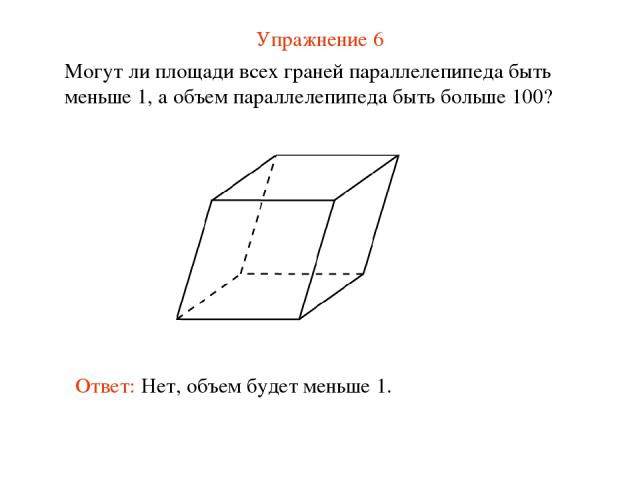
Упражнение 6 Могут ли площади всех граней параллелепипеда быть меньше 1, а объем параллелепипеда быть больше 100? Ответ: Нет, объем будет меньше 1.

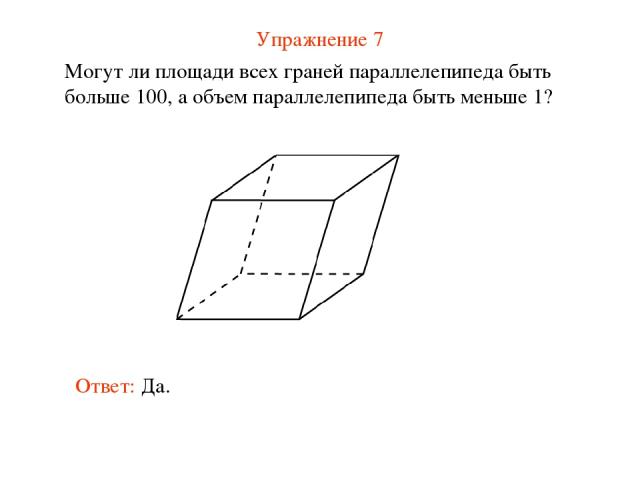
Упражнение 7 Могут ли площади всех граней параллелепипеда быть больше 100, а объем параллелепипеда быть меньше 1? Ответ: Да.

Упражнение 8* Какой наибольший объем может иметь параллелепипед, сумма длин ребер которого, выходящих из одной вершины, равна 1?

Упражнение 9* В пространстве даны три параллелепипеда. Как провести плоскость, чтобы она разделила каждый параллелепипед на две части равного объема? Ответ: Плоскость, проходящая через центры симметрии параллелепипедов.

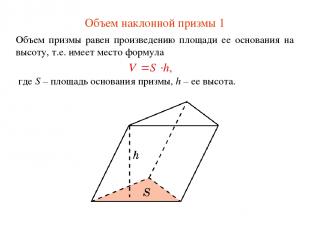
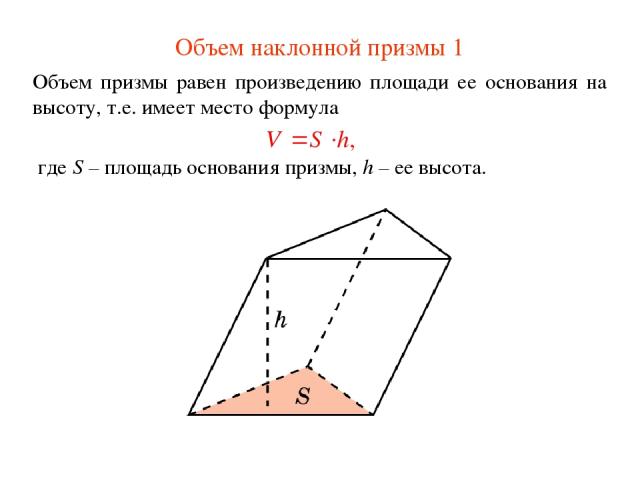
Объем наклонной призмы 1 Объем призмы равен произведению площади ее основания на высоту, т.е. имеет место формула где S – площадь основания призмы, h – ее высота.

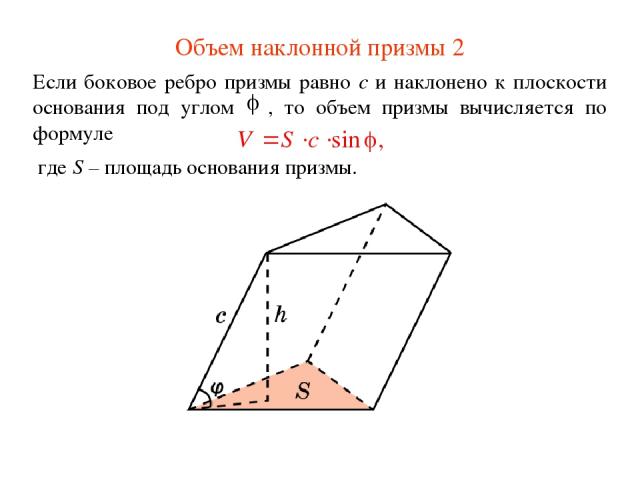
Объем наклонной призмы 2 Если боковое ребро призмы равно c и наклонено к плоскости основания под углом , то объем призмы вычисляется по формуле где S – площадь основания призмы.

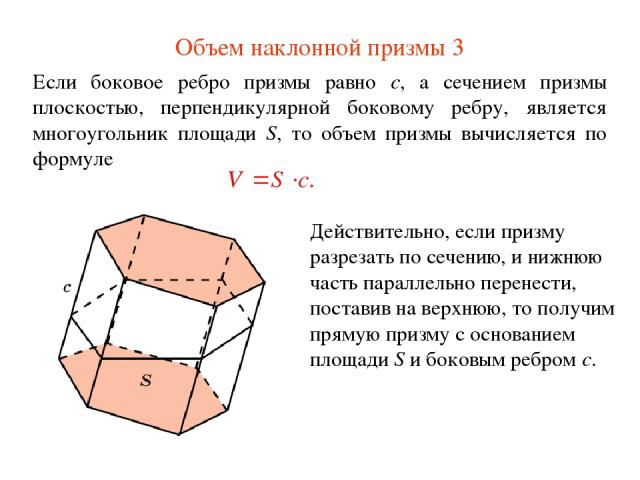
Объем наклонной призмы 3 Если боковое ребро призмы равно c, а сечением призмы плоскостью, перпендикулярной боковому ребру, является многоугольник площади S, то объем призмы вычисляется по формуле

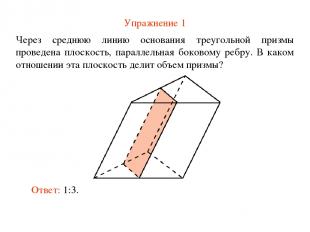
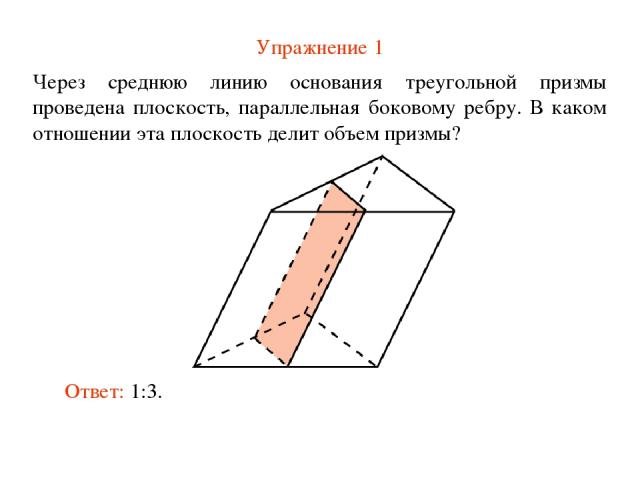
Упражнение 1 Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. В каком отношении эта плоскость делит объем призмы? Ответ: 1:3.

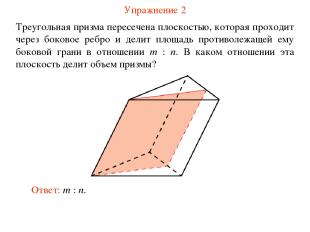
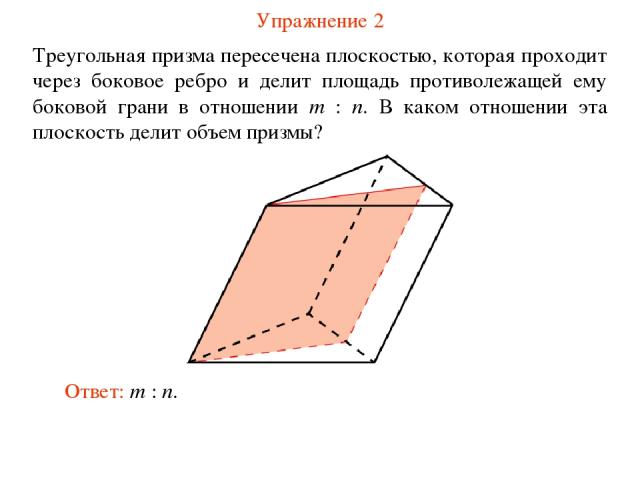
Упражнение 2 Треугольная призма пересечена плоскостью, которая проходит через боковое ребро и делит площадь противолежащей ему боковой грани в отношении m : n. В каком отношении эта плоскость делит объем призмы? Ответ: m : n.

Упражнение 3 В наклонной треугольной призме площадь одной из боковых граней равна Q, а расстояние от нее до противоположного ребра равно d. Найдите объем призмы.

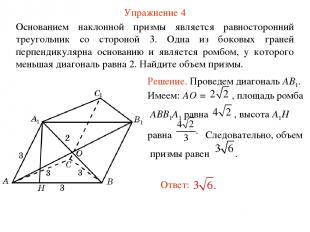
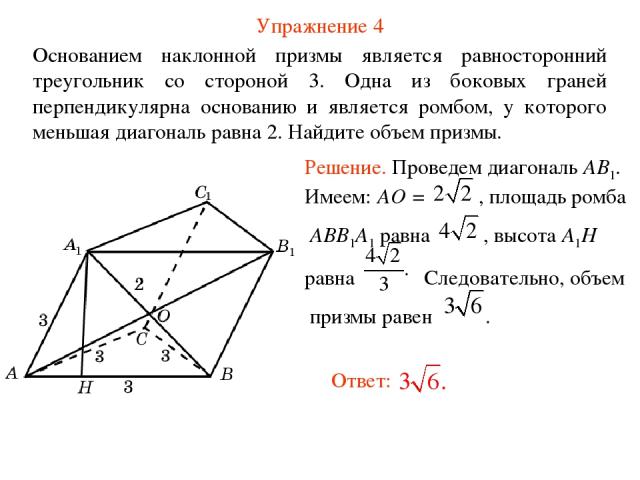
Упражнение 4 Основанием наклонной призмы является равносторонний треугольник со стороной 3. Одна из боковых граней перпендикулярна основанию и является ромбом, у которого меньшая диагональ равна 2. Найдите объем призмы.

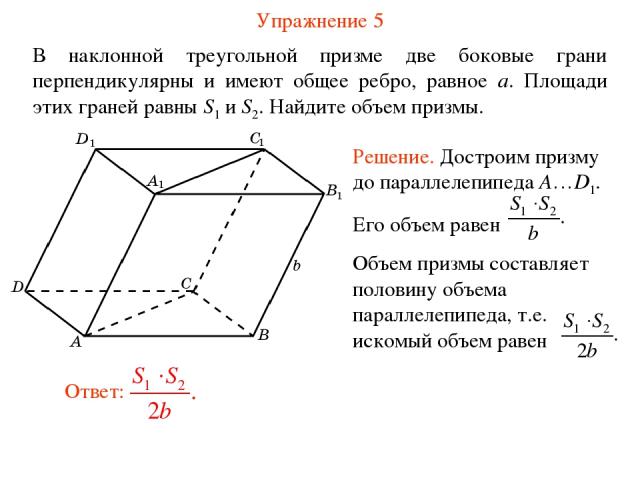
Упражнение 5 В наклонной треугольной призме две боковые грани перпендикулярны и имеют общее ребро, равное a. Площади этих граней равны S1 и S2. Найдите объем призмы.

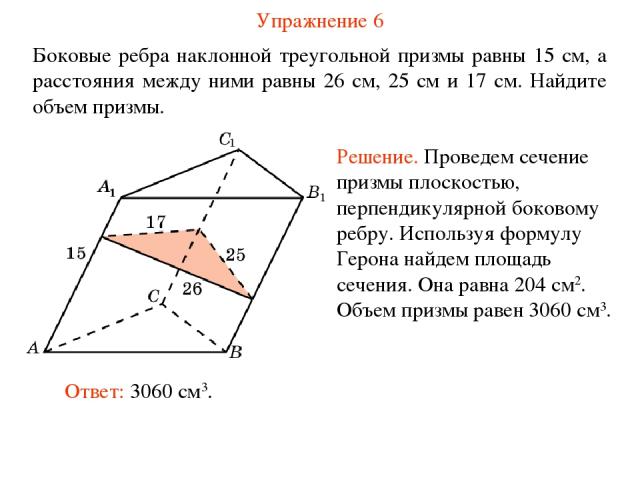
Упражнение 6 Боковые ребра наклонной треугольной призмы равны 15 см, а расстояния между ними равны 26 см, 25 см и 17 см. Найдите объем призмы.

Упражнение 7 Основанием призмы является параллелограмм со сторонами 1, 2 и острым углом 30о. Боковые ребра равны 3 и составляют с плоскостью основания угол 45о. Найдите объем призмы.

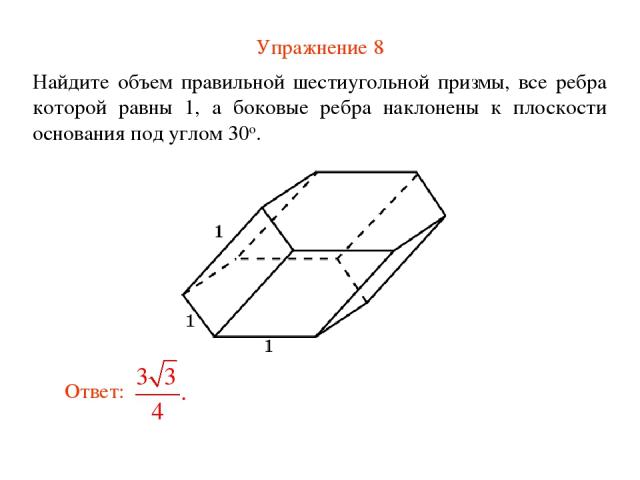
Упражнение 8 Найдите объем правильной шестиугольной призмы, все ребра которой равны 1, а боковые ребра наклонены к плоскости основания под углом 30о.

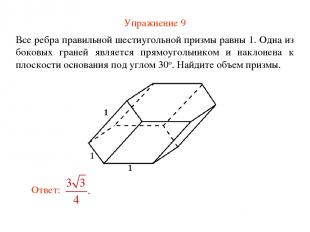
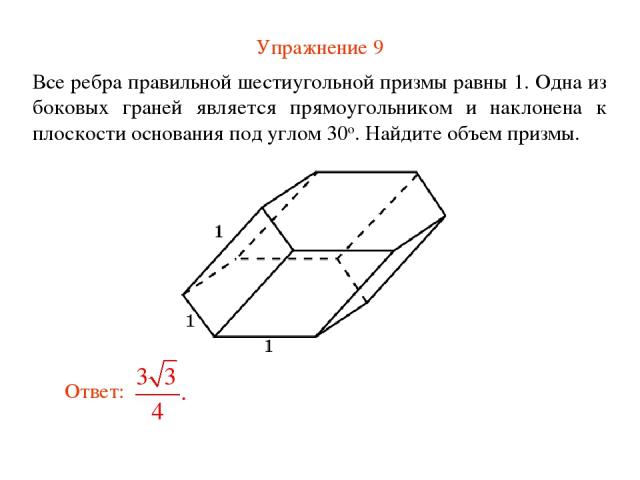
Упражнение 9 Все ребра правильной шестиугольной призмы равны 1. Одна из боковых граней является прямоугольником и наклонена к плоскости основания под углом 30о. Найдите объем призмы.

Упражнение 10 В основаниях призмы квадраты. Верно ли, что любая плоскость, проходящая через центры квадратов, делит призму на две равновеликие части? Ответ: Да.

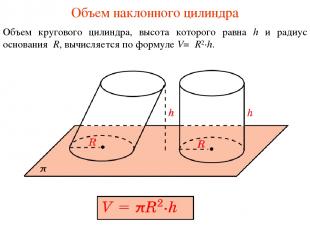
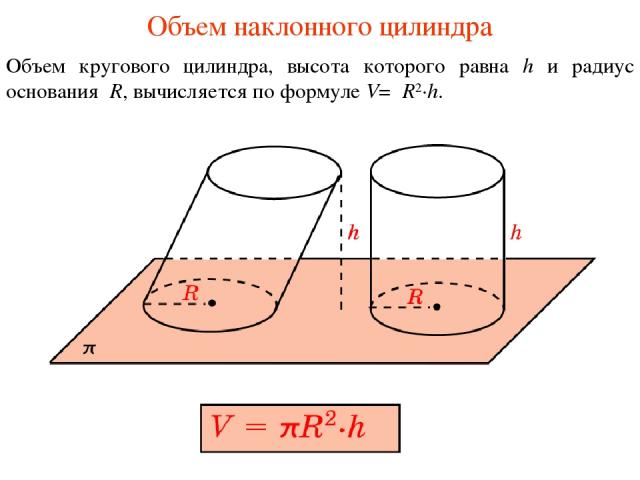
Объем наклонного цилиндра Объем кругового цилиндра, высота которого равна h и радиус основания R, вычисляется по формуле V=πR2·h.

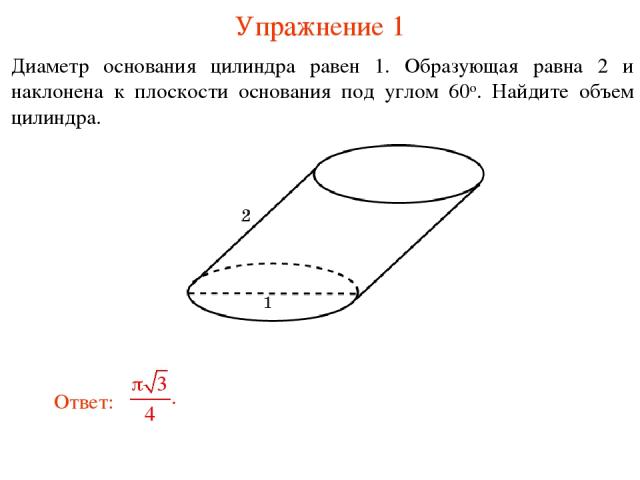
Упражнение 1 Диаметр основания цилиндра равен 1. Образующая равна 2 и наклонена к плоскости основания под углом 60о. Найдите объем цилиндра.

Упражнение 2 Верно ли, что любая плоскость, проходящая через центры оснований кругового цилиндра, делит его на равновеликие части? Ответ: Да.

Упражнение 3 Два цилиндра имеют равные высоты, а площадь основания одного в два раза больше площади основания другого. Как относятся их объемы? Ответ: 2:1.

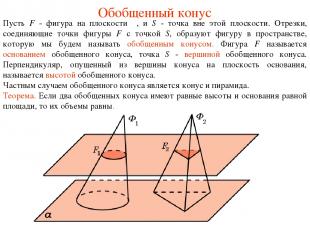
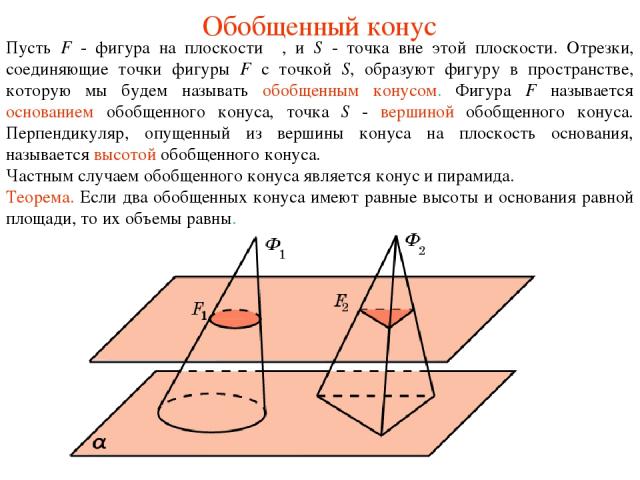
Обобщенный конус Пусть F - фигура на плоскости π, и S - точка вне этой плоскости. Отрезки, соединяющие точки фигуры F с точкой S, образуют фигуру в пространстве, которую мы будем называть обобщенным конусом. Фигура F называется основанием обобщенного конуса, точка S - вершиной обобщенного конуса. Перпендикуляр, опущенный из вершины конуса на плоскость основания, называется высотой обобщенного конуса. Частным случаем обобщенного конуса является конус и пирамида. Теорема. Если два обобщенных конуса имеют равные высоты и основания равной площади, то их объемы равны.

Упражнение 1 Верно ли, что две пирамиды, имеющие общее основание и вершины, расположенные в плоскости, параллельной основанию, равновелики? Ответ: Да.

Упражнение 2 Два конуса имеют равные высоты, а площадь основания одного в три раза больше площади основания другого. Как относятся их объемы? Ответ: 3:1.

Упражнение 3 Верно ли, что любая плоскость, проходящая через вершину и центр основания кругового конуса, делит его на равновеликие части? Ответ: Да.

Упражнение 4 В основании пирамиды квадрат. Верно ли, что любая плоскость, проходящая через вершину пирамиды и центр основания, делит пирамиду на две равновеликие части? Ответ: Да.