Презентация на тему: Окружность 8 класс

Вписанная окружность Урок геометрии в 8 классе 900igr.net

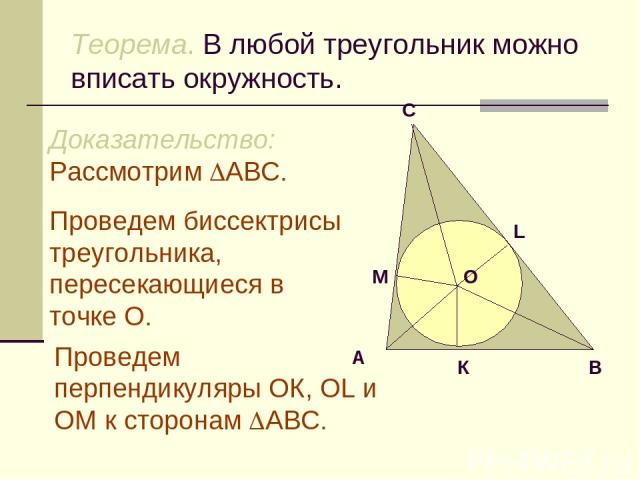
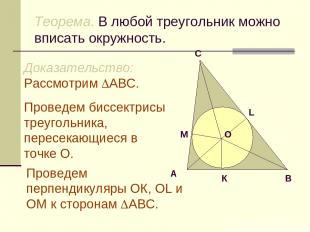
Теорема. В любой треугольник можно вписать окружность. Доказательство: Рассмотрим АВС. Проведем биссектрисы треугольника, пересекающиеся в точке О. Проведем перпендикуляры ОК, ОL и ОM к сторонам АВС.

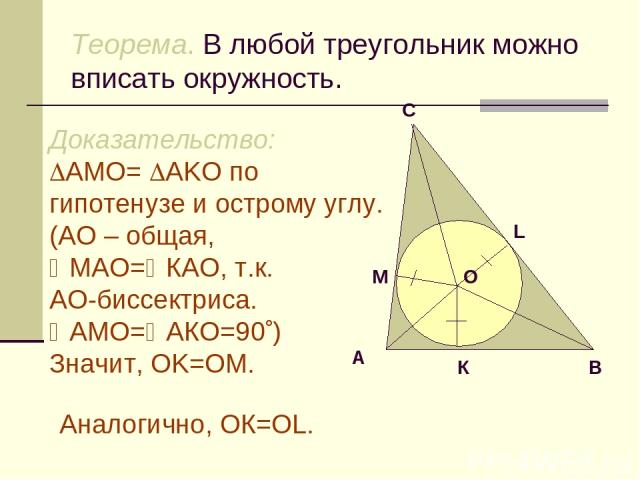
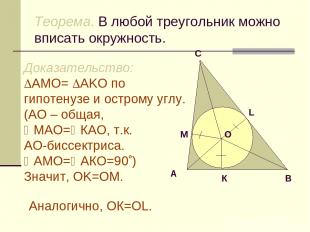
Теорема. В любой треугольник можно вписать окружность. Доказательство: АMO= АKO по гипотенузе и острому углу. (AO – общая, МАО= КАО, т.к. АО-биссектриса. АМО= АКО=90 ) Значит, OK=OM. Аналогично, ОК=OL.

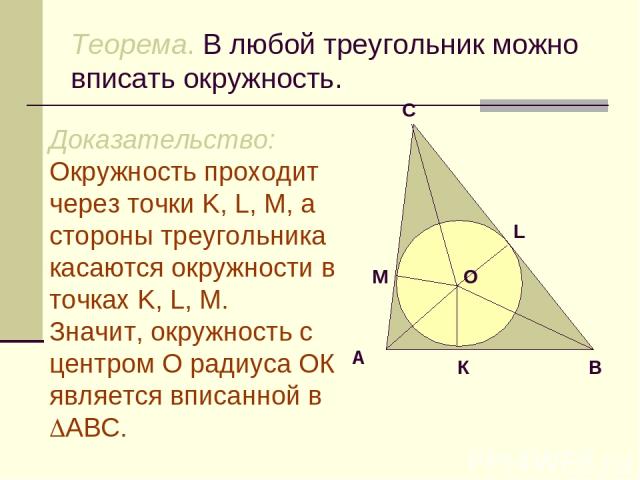
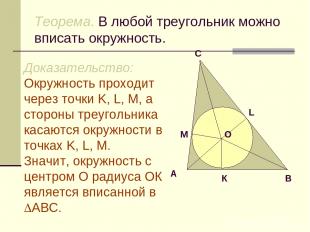
Теорема. В любой треугольник можно вписать окружность. Доказательство: Окружность проходит через точки K, L, M, а стороны треугольника касаются окружности в точках K, L, M. Значит, окружность с центром О радиуса ОК является вписанной в АВС.

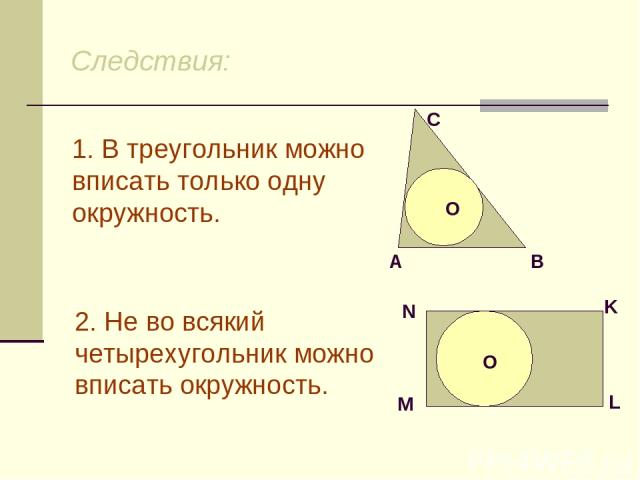
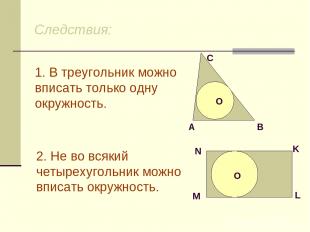
Следствия: