Презентация на тему: Угол, вписанный в окружность

Вписанный угол Теорема о вписанном угле 900igr.net

Цели урока: сформировать понятие вписанного угла, изучить теорему о вписанном угле; формирование навыков самостоятельной работы с учебником.

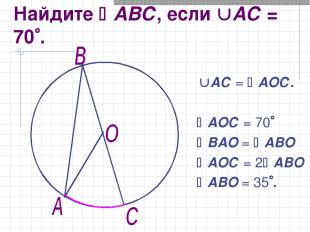
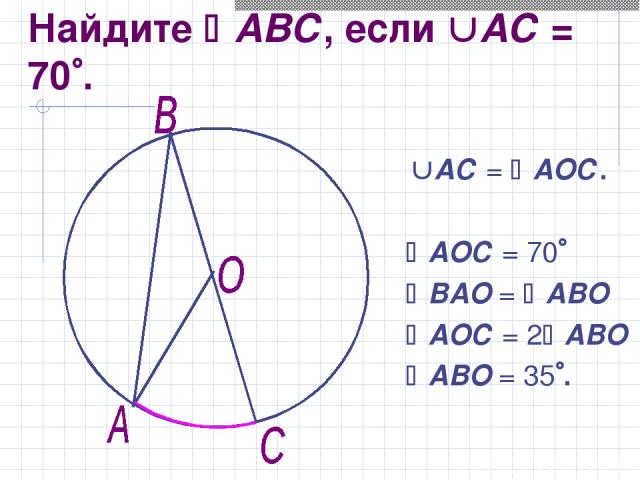
Найдите АВС, если АС = 70 . АС = АОС. АОС = 70 ВАО = АВО АОС = 2 АВО АВО = 35 .

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. АВС вписанный: 1) вершина В лежит на окружности; 2) сторона ВА пересекает окружность; 3) сторона ВС пересекает окружность.

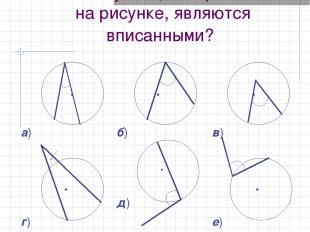
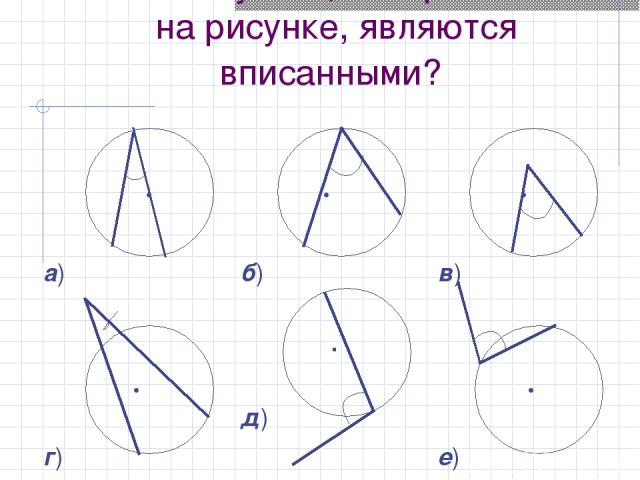
Какие из углов, изображенных на рисунке, являются вписанными?     а)     б)      в)     г)   . д)     е)

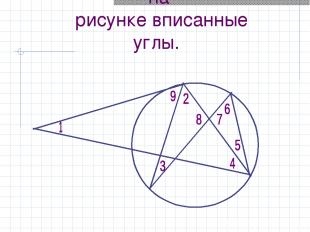
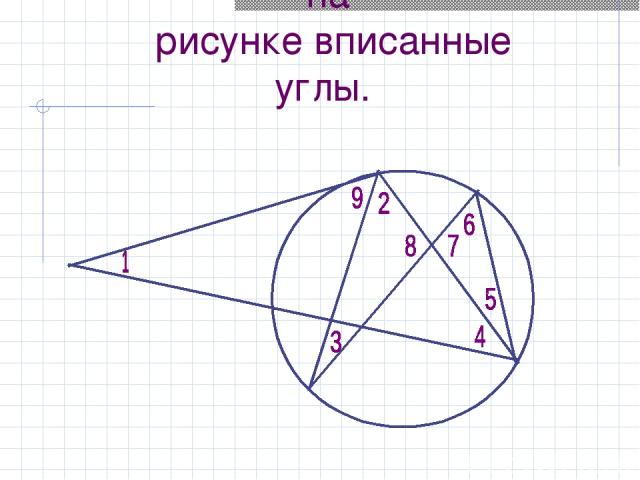
Укажите изображенные на рисунке вписанные углы.

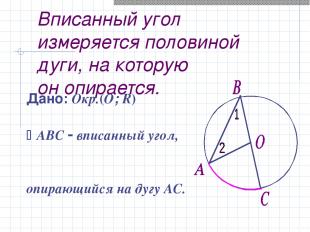
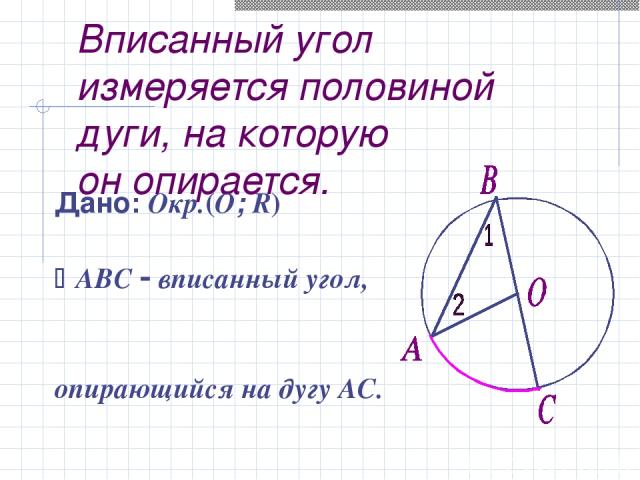
Вписанный угол измеряется половиной дуги, на которую он опирается. Дано: Окр.(O; R) ABC вписанный угол, опирающийся на дугу АС. Доказать: АВС = ½ АС Док - во:

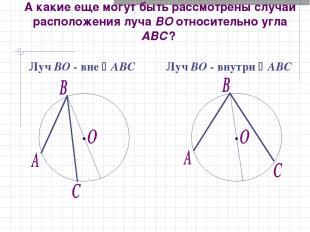
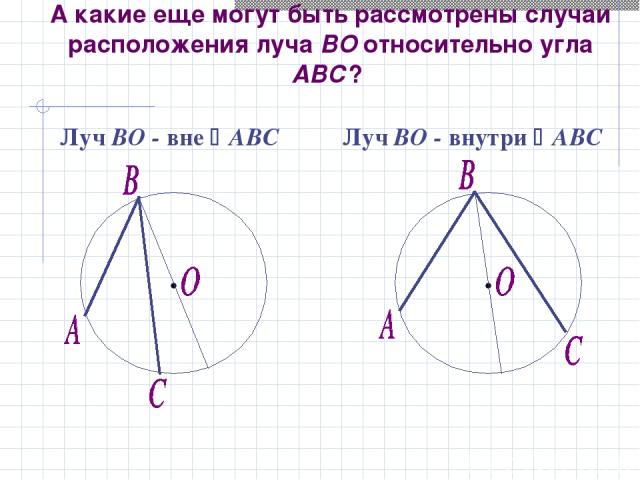
А какие еще могут быть рассмотрены случаи расположения луча ВО относительно угла АВС? Луч ВО - вне АВС Луч ВО - внутри АВС

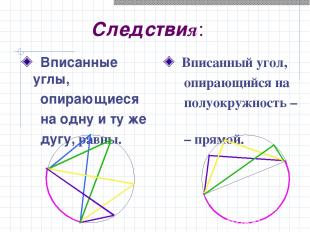
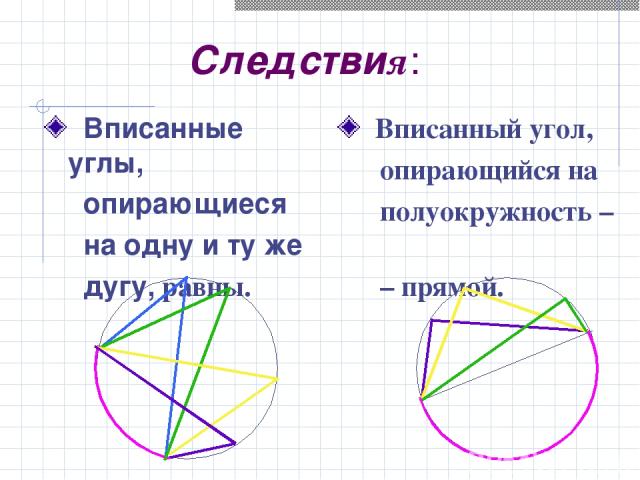
Следствия: Вписанные углы, опирающиеся на одну и ту же дугу, равны. Вписанный угол, опирающийся на полуокружность – – прямой.

Итоги урока - Какой угол называется центральным? - Чему равна градусная мера центрального угла? - Какой угол называется вписанным? - Чему равна градусная мера вписанного угла? - Что можно сказать о градусной мере вписанных углов, опирающихся на одну и ту же дугу? - Чему равна градусная мера вписанного угла, опирающегося на полуокружность?

Домашнее задание п. 71; вопросы 11-13 (стр.187), № 657, № 660.