Презентация на тему: Тригонометрические функции тупого угла

Тригонометрические функции тупого угла Определим тригонометрические функции углов 90о A < 180, положив: sin 90о = 1 и sin A = sin(180о–A); cos 90о = 0 и cos A = –cos(180о–A). Тангенс и котангенс углов определяются как и ранее, а именно, tg A = ctg A = 900igr.net

Упражнение 1 Может ли быть отрицательным: а) синус; б) косинус; в) тангенс; г) котангенс тупого угла? Ответ: а) Нет; б) да; в) да; г) да.
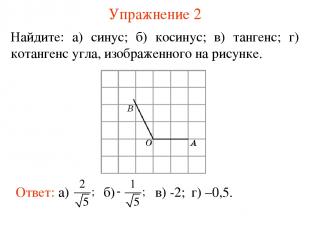
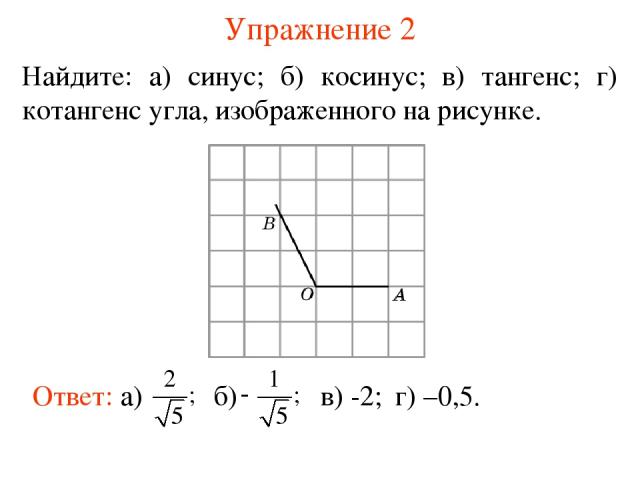
Упражнение 2 Найдите: а) синус; б) косинус; в) тангенс; г) котангенс угла, изображенного на рисунке. в) -2; г) –0,5.
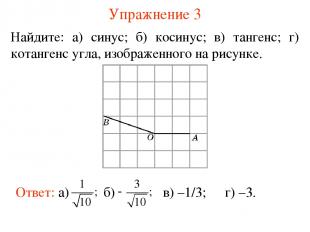
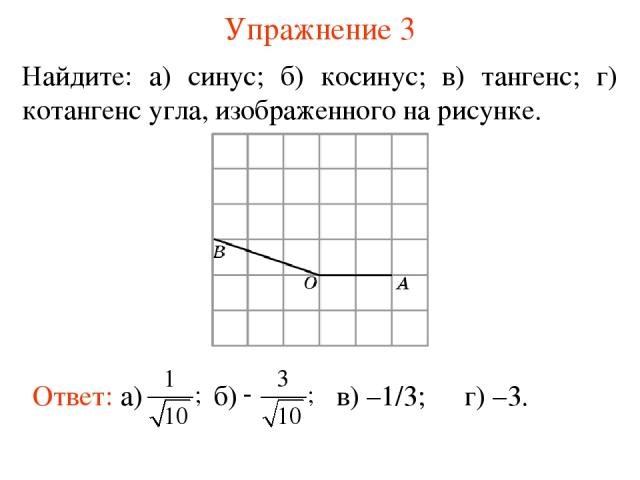
Упражнение 3 Найдите: а) синус; б) косинус; в) тангенс; г) котангенс угла, изображенного на рисунке. в) –1/3; г) –3.
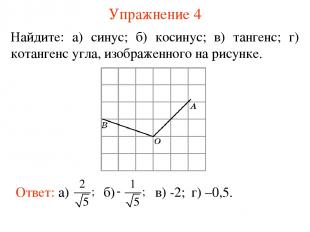
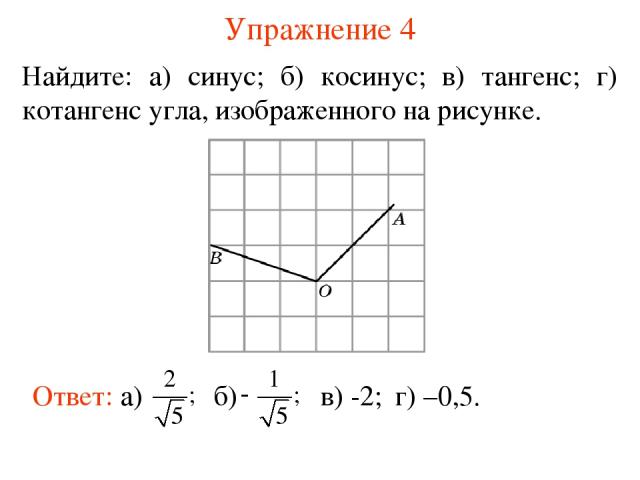
Упражнение 4 Найдите: а) синус; б) косинус; в) тангенс; г) котангенс угла, изображенного на рисунке. в) -2; г) –0,5.

Упражнение 5 Найдите синус, косинус, тангенс и котангенс углов: а) 120о; б) 135о; в) 150о.

Упражнение 6 Найдите tg A, если: а) cos A = ; б) cos A = ; в) sin A = и 90о < A < 180о. в) –1.

Упражнение 7 Известно, что tg A = . Найдите sin A и cos A.

Упражнение 8 Найдите sin A и cos A, если tg A + ctg A = .

Упражнение 9 Расположите в порядке возрастания тангенсы углов: 70о, 80о, 100о. Ответ: tg 100о < tg 70о < tg 80о.

Упражнение 10 Расположите в порядке возрастания котангенсы углов: 60о, 110о, 120о. Ответ: ctg 120о < ctg 110о < tg 60о.

Упражнение 11 Даны два смежных угла. Чему равна сумма их: а) тангенсов; б) котангенсов? Ответ: а) 0; б) 0.