Презентация на тему: Вписанные в окружность и описанные около окружности четырехугольники

Вписанные в окружность и описанные около окружности четырехугольники.

Четырехугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность называется описанной около четырехугольника.

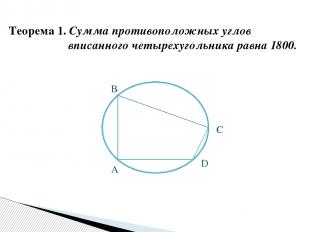
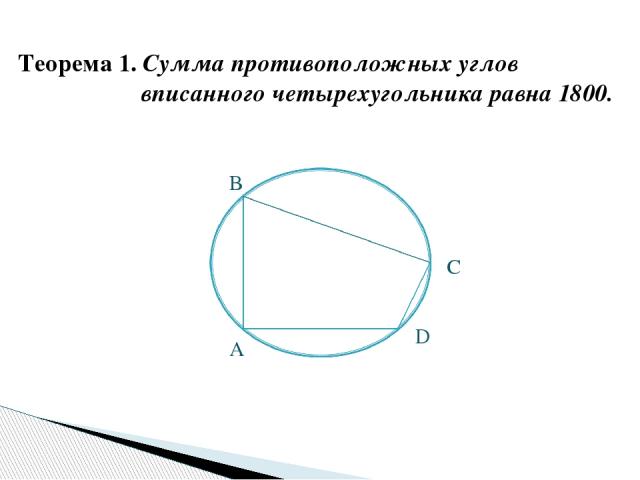
Теорема 1. Сумма противоположных углов вписанного четырехугольника равна 1800. А D С B

Теорема обратная теореме 1. Если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность. Следствие. Не во всякий четырёхугольник можно вписать окружность.

Если все стороны четырехугольника касаются окружности, то он называется четырёхугольником, описанным около этой окружности, а окружность - вписанной в четырёхугольник.

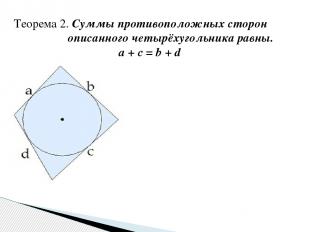
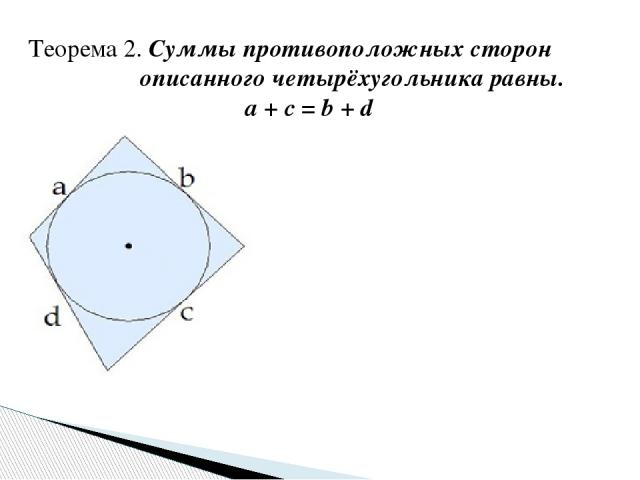
Теорема 2. Суммы противоположных сторон описанного четырёхугольника равны.    a + c = b + d

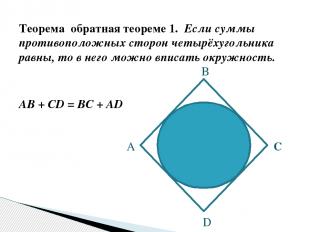
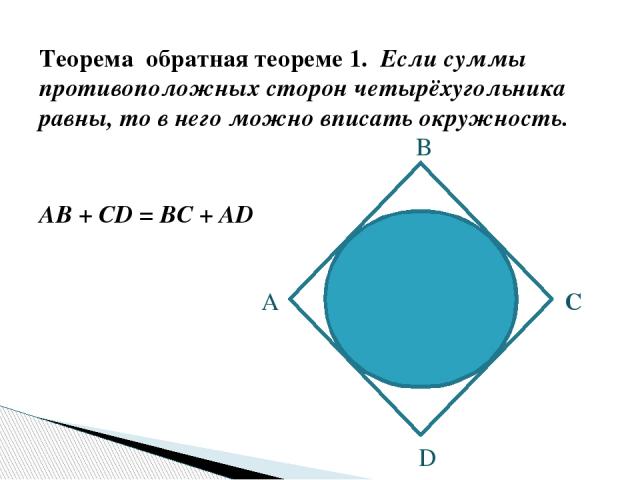
Теорема обратная теореме 1.  Если суммы противоположных сторон четырёхугольника равны, то в него можно вписать окружность. AB + CD = BC + AD А B C D

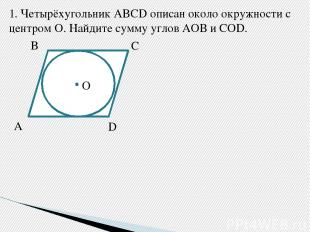
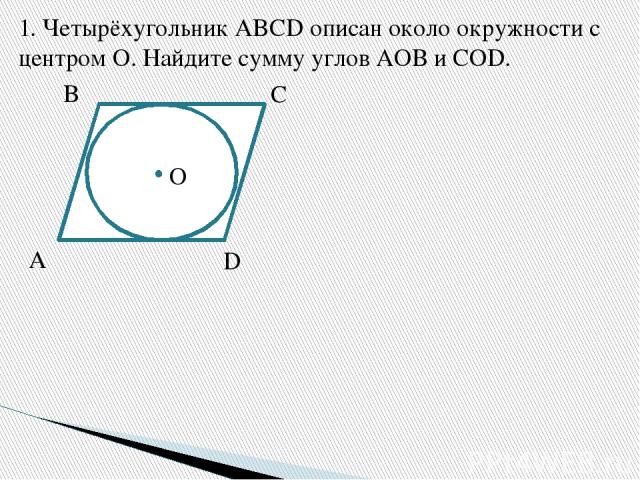
1. Четырёхугольник ABCD описан около окружности с центром О. Найдите сумму углов АОВ и COD. A B C D O

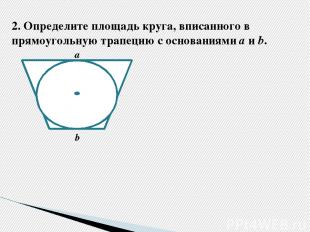
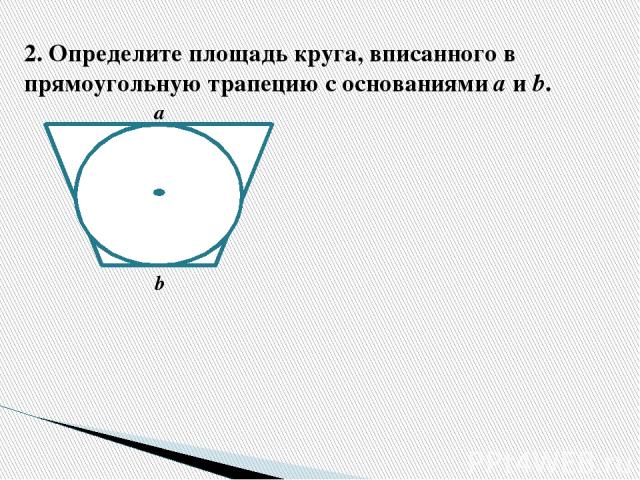
2. Определите площадь круга, вписанного в прямоугольную трапецию с основаниями а и b. а b