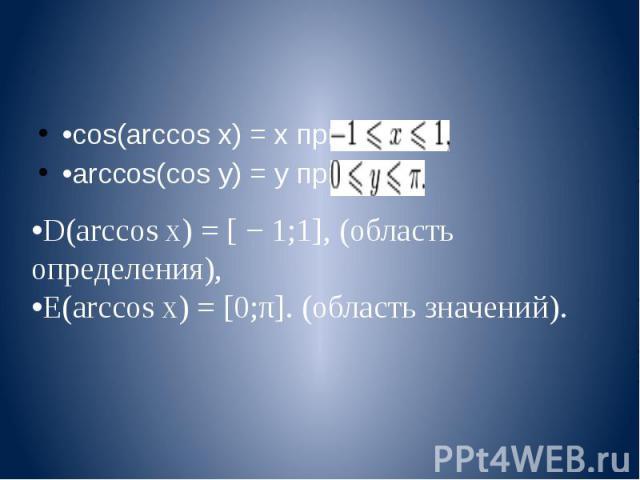Презентация на тему: Тригонометрия

ПРЕЗЕНТАЦИЯ ПО МАТЕМАТИКЕ НА ТЕМУ ТРИГОНОМЕТРИЯ.

Тригонометрия тригономе трия (от греч.τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика БартоломеусаПитискуса (BartholomäusPitiscus, 1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.

Применение тригонометрии   Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

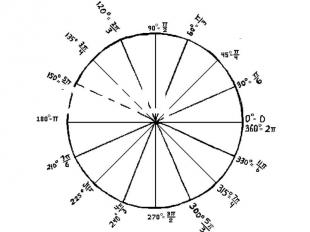
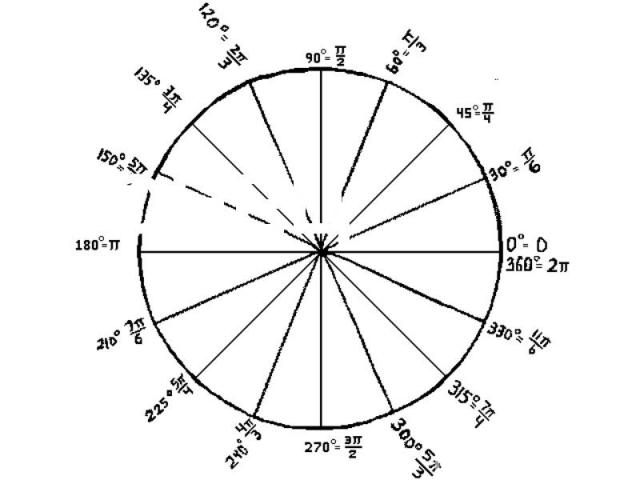
Числовая окружность

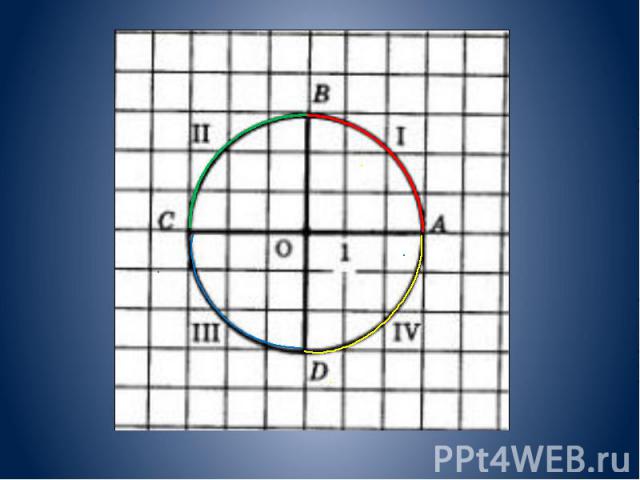
Тригонометрический круг— построенная на плоскости с прямоугольными декартовыми координатами окружность, имеющая центр в точке начала координат и единичный радиус, т.е. единичная окружность, которая используется для геометрического определения тригонометрических функций. Название «тригонометрический круг» не совсем удачно, поскольку речь идёт об окружности, а не о круге; тем не менее, часто используется именно это название. Тригонометрический круг— построенная на плоскости с прямоугольными декартовыми координатами окружность, имеющая центр в точке начала координат и единичный радиус, т.е. единичная окружность, которая используется для геометрического определения тригонометрических функций. Название «тригонометрический круг» не совсем удачно, поскольку речь идёт об окружности, а не о круге; тем не менее, часто используется именно это название.

Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме. Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.

Тригонометрические тождества Тригонометрические тождества — математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента

Основные тригонометрические формулы

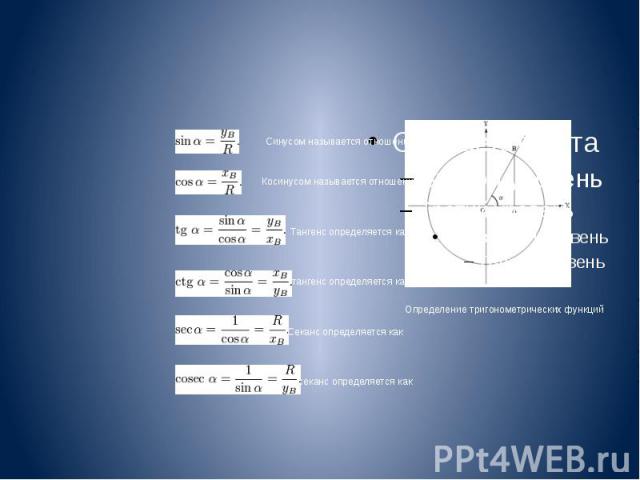
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:

Непрерывность Синус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва

Чётность Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Периодичность Функции

ТРЕГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Тригонометри ческие фу нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.

: К тригонометрическим функциям относятся:  во-первых, прямые тригонометрические функции синус (sin x), косинус (cos x);   во-вторых, противоположные им тригонометрические функции: секанс (sec x) косеканс (cosec x);   и, в-третьих, производные тригонометрические функции: тангенс (tg x), котангенс (ctg x).

  Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника). Синус — отношение противолежащего катета к гипотенузе. Косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение противолежащего катета к прилежащему. Котангенс — отношение прилежащего катета к противолежащему. Секанс — отношение гипотенузы к прилежащему катету. Косеканс — отношение гипотенузы к противолежащему катету.

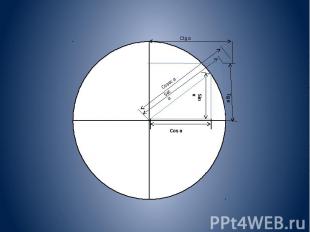
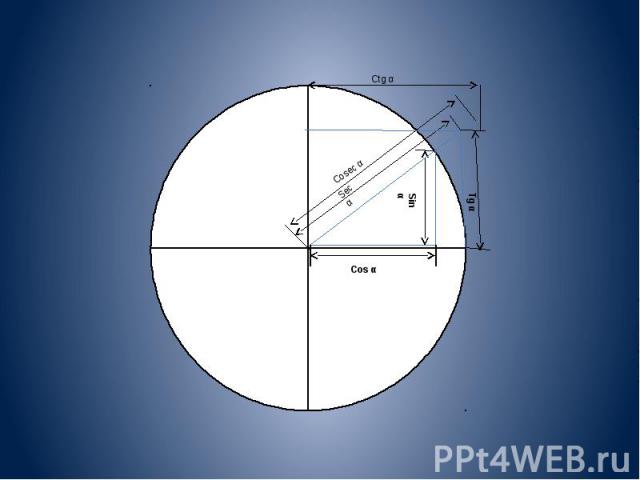
    Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса и отложим от горизонтальной оси угол θ (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда: Синус угла θ определяется как ордината точки A. Косинус — абсцисса точки A. Тангенс — отношение синуса к косинусу. Котангенс — отношение косинуса к синусу (то есть величина, обратная тангенсу). Секанс — величина, обратная косинусу. Косеканс — величина, обратная синусу.

Синус и косинус вещественного аргумента являются периодическими непрерывными и неограниченно дифференцируемыми вещественнозначными функциями. Остальные четыре функции на вещественной оси также вещественнозначные, периодические и неограниченно дифференцируемые на области определения, но не непрерывные. Тангенс и секанс имеют разрывы второго рода в точках ±πn + π/2, а котангенс и косеканс — в точках ±πn. Синус и косинус вещественного аргумента являются периодическими непрерывными и неограниченно дифференцируемыми вещественнозначными функциями. Остальные четыре функции на вещественной оси также вещественнозначные, периодические и неограниченно дифференцируемые на области определения, но не непрерывные. Тангенс и секанс имеют разрывы второго рода в точках ±πn + π/2, а котангенс и косеканс — в точках ±πn.

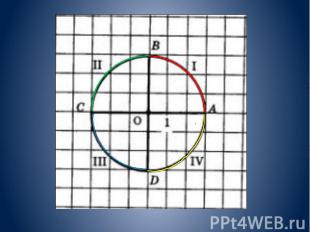
Определение тригонометрических функций   Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB

Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB.

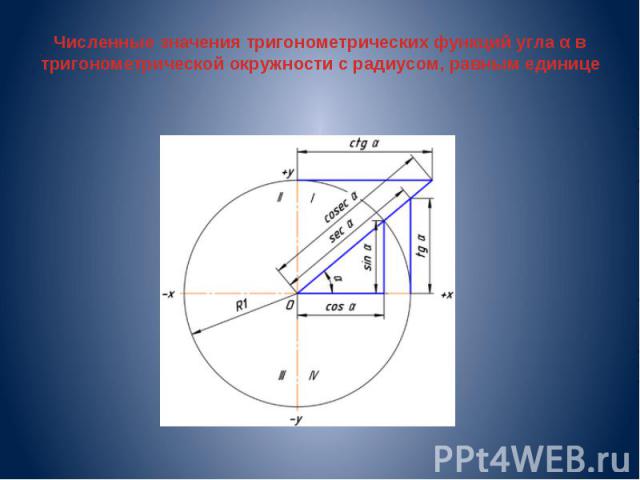
Численные значения тригонометрических функций угла α в тригонометрической окружности с радиусом, равным единице

Тригонометрические функции острого угла Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда: Синусом угла α называется отношение AB/OB (отношение противолежащего катета к гипотенузе). Косинусом угла α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе). Тангенсом угла α называется отношение AB/OA (отношение противолежащего катета к прилежащему). Котангенсом угла α называется отношение ОА/AB (отношение прилежащего катета к противолежащему). Секансом угла α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету). Косекансом угла α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету).

Определение тригонометрических функций как решений дифференциальных уравнений Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения

Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:

Определение тригонометрических функций через ряды Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны х рядов:

Пользуясь этими формулами, а также уравнениями Пользуясь этими формулами, а также уравнениями

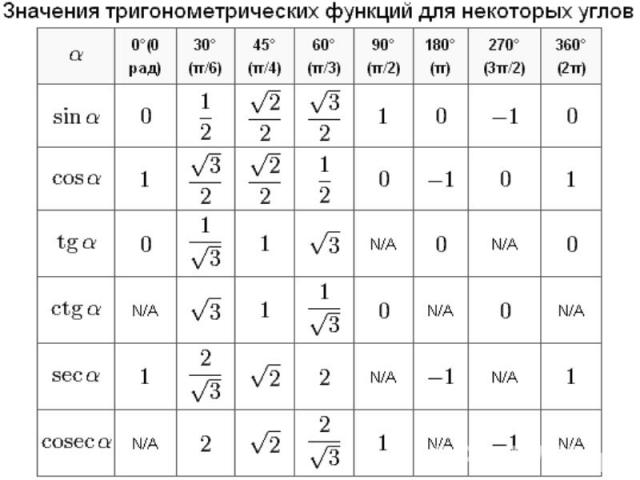
Значения тригонометрических функций для некоторых углов Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («N/A» означает, что это значение не определено).

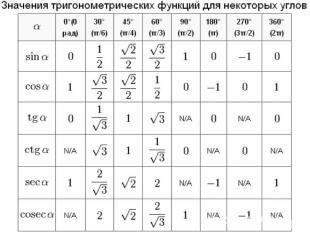
Значения тригонометрических функций нестандартных углов

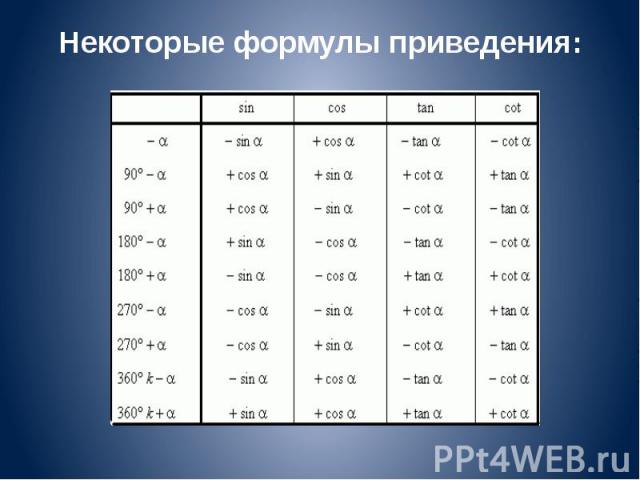
Формулы приведения ♦ Формулами приведения называются формулы следующего вида:

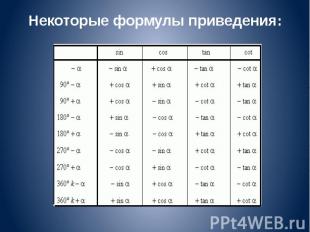
Некоторые формулы приведения:

Формулы сложения

Аналогичные формулы для суммы трёх углов:

Формулы двойного угла:

Формулы тройного угла:

Формулы половинного угла:

Произведения     ♦ Формулы для произведений функций двух углов:

Аналогичные формулы для произведений синусов и косинусов трёх углов:

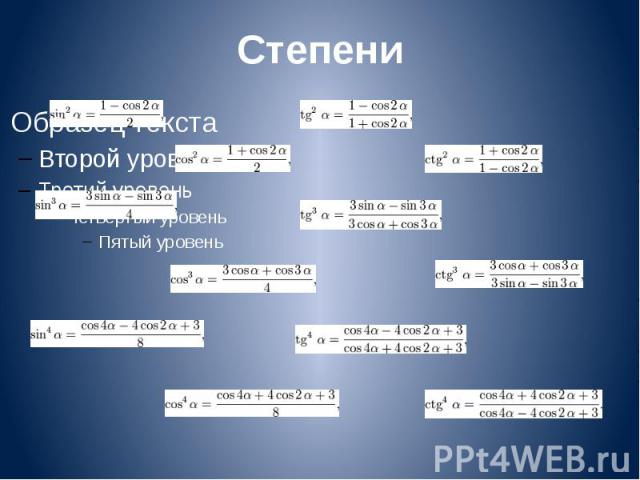
Степени

Суммы

Для функций от аргумента x существует представление: Для функций от аргумента x существует представление:

Однопараметрическое представление Все тригонометрические функции можно выразить через тангенс половинного угла.

Производные и интегралы Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:

Тригонометрические функции комплексного аргумента Формула Эйлера:

Комплексные синус и косинус тесно связаны с гиперболическими функциями: Комплексные синус и косинус тесно связаны с гиперболическими функциями:

Комплексные графики   На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте

Тригонометрические функции в комплексной плоскости

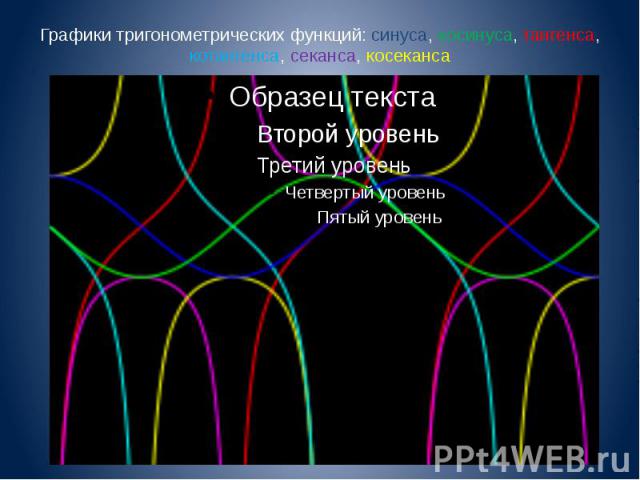
Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса

Обратные тригонометрические функции Обра тные тригонометри ческие фу нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций: аркси нус (обозначение: arcsin) аркко синус (обозначение: arccos) аркта нгенс (обозначение: arctg; в иностранной литературе arctan) арккота нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan) арксе канс (обозначение: arcsec) арккосе канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1 для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1. Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1 для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1.

Основное соотношение Основное соотношение

Функция arcsin Арксинусом числа m называется такое значение угла x, для которого

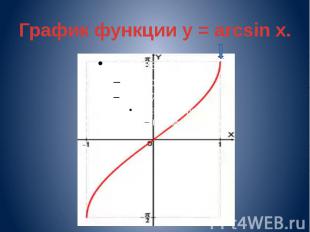
График функции y = arcsin x.

Свойства функции arcsin

Получение функции arcsin   Дана функция y = sin x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arcsinx функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений Так как для функции y = sin x на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsin x, график которой симметричен графику функции y = sin x на отрезке относительно прямой y = x.

Функция arccos Арккосинусом числа m называется такое значение угла x, для которого

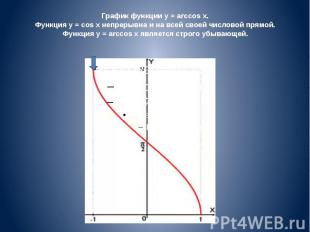
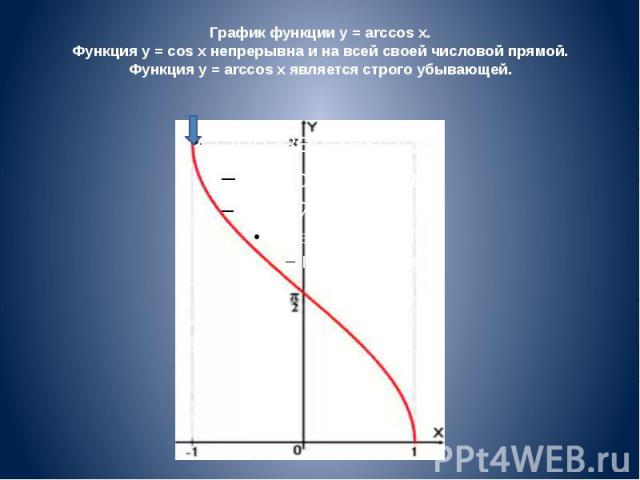
График функции y = arccos x. Функция y = cos x непрерывна и на всей своей числовой прямой. Функция y = arccos x является строго убывающей.

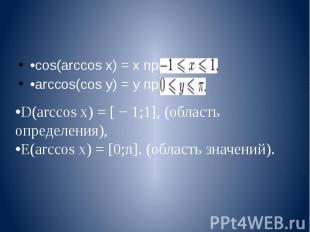
•cos(arccos x) = x при •arccos(cos y) = y при

Свойства функции arccos ♦

Получение функции arccos Дана функция y = cos x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — [0;π]. На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π] существует обратная функция y = arccos x, график которой симметричен графику y = cos x на отрезке [0;π] относительно прямой y = x.

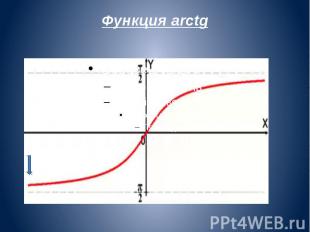
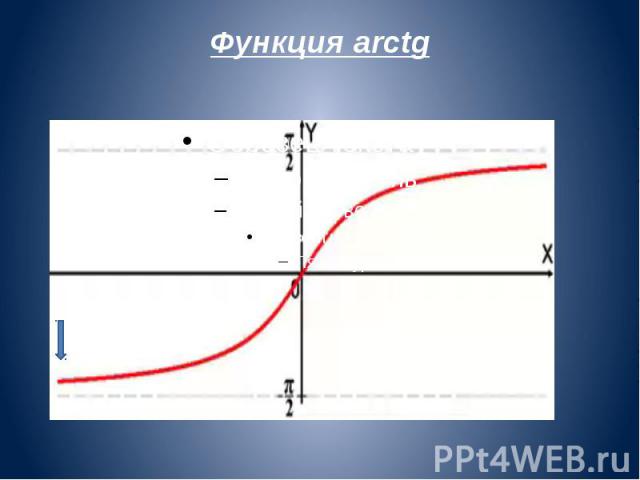
Функция arctg

Арктангенсом числа m называется такое значение угла α, для которого Арктангенсом числа m называется такое значение угла α, для которого

Свойства функции arctg

Получение функции arctg Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз _ На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная график которой симметричен графику на отрезке относительно прямой y = x.

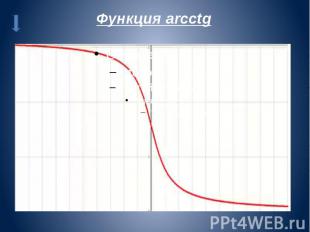
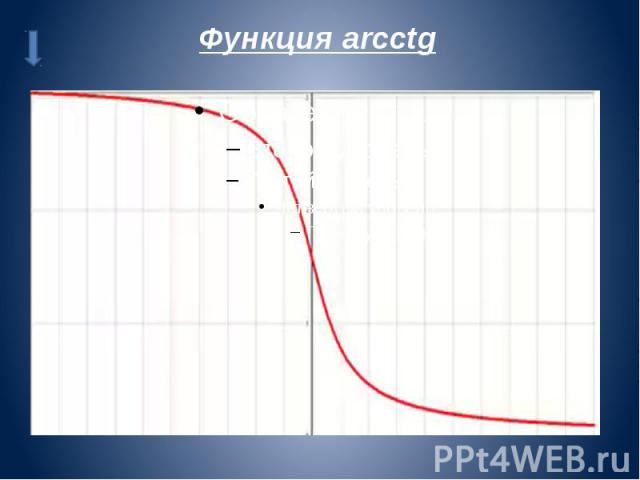
Функция arcctg

функции y=arcctg x Арккотангенсом числа m называется такое значение угла x, для которого

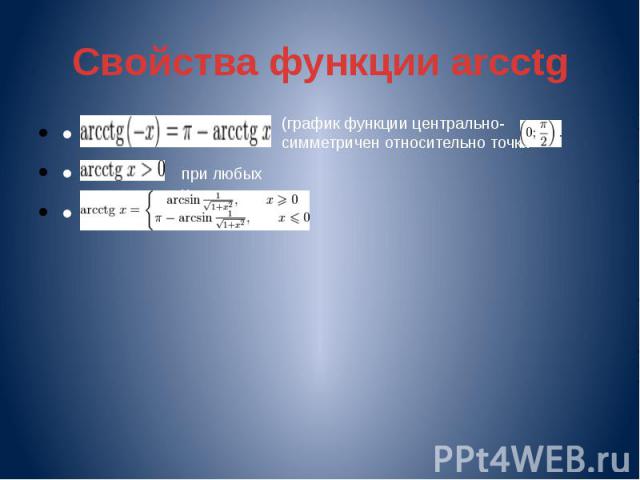
Свойства функции arcctg • • •

Получение функции arcctg   Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — (0;π). На этом отрезке строго убывает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция , график которой симметричен графику на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсу

Функция arcsec

Производные от обратных тригонометрических функций

Интегралы от обратных тригонометрических функций

Для действительных x ≥ 1: Для действительных x ≥ 1:

ИСПОЛЬЗОВАНИЕ В ГЕОМЕТРИИ Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.

В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол: В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол: α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)

•sin x = a.  •sin x = a.  Если | a | > 1 — вещественных решений нет. Если — решением является число вида •cos x = a. Если | a | > 1 — решений нет. Если —решением является число вида

• Решением является число вида • Решением является число вида

Универсальная тригонометрическая подстановка Тождества имеют смысл, только когда существуют обе части (то есть при ).

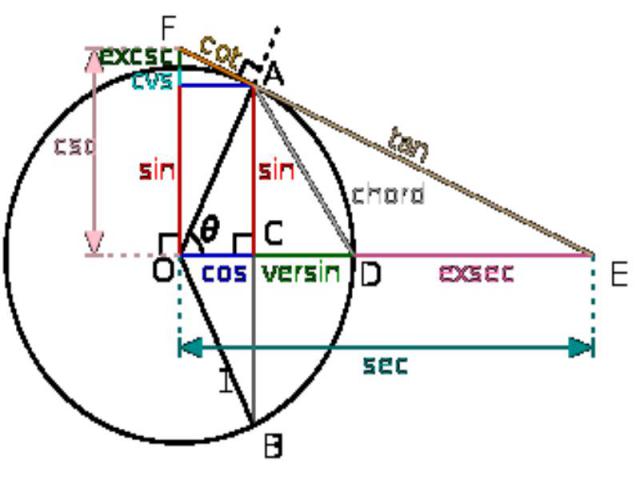
Редко используемые тригонометрические функции   Редко используемые тригонометрические функции — функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом, секансом и косекансом). К ним относятся:

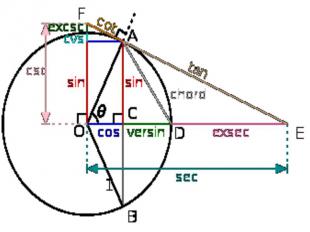
Определение тригонометрических функций через окружность. Отрезки CD и DE описывают соответственно версинус и эксеканс. Определение тригонометрических функций через окружность. Отрезки CD и DE описывают соответственно версинус и эксеканс.

•Гаверсинус (англ. haversinus, сокращениеот half the versed sine).Определяется как •Гаверсинус (англ. haversinus, сокращениеот half the versed sine).Определяется как

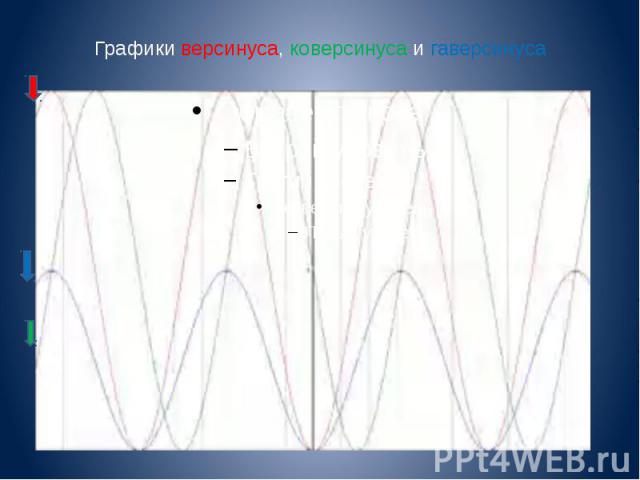
Использование Версинус, коверсинус и гаверсинус были удобны для ручных расчётов с использованием логарифмов, поскольку они всюду неотрицательны, однако в связи с развитием вычислительных средств эта область применения неактуальна. В настоящее время эти функции используются для описания соответствующих сигналов в электронике (например, в функциональных генераторах). Гаверсинус также используется в навигационных расчётах для избежания ошибок округления в вычислительных системах с ограниченной разрядностью.

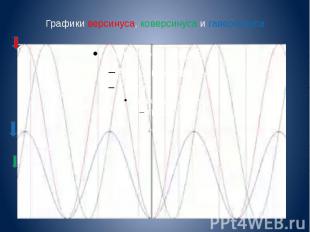
Графики версинуса, коверсинуса и гаверсинуса

Рассуждая аналогичным образом, делаем вывод, что на единичной окружности можно найти и точку Ег, для которой АЕ, = 1, и точку Е2, для которой АЕг = 2, и точку Е3, для которой АЕ3 = 3, и точку Е4, для которой АЕ4 = 4, и точку Еь, для которой АЕЪ = 5, и точку Е6, для которой АЕ6 = 6. На рис. 102 отмечены (приблизительно) соответствующие точки (причем для ориентировки каждая из четвертей единичной окружности разделена черточками на три равные части). Рассуждая аналогичным образом, делаем вывод, что на единичной окружности можно найти и точку Ег, для которой АЕ, = 1, и точку Е2, для которой АЕг = 2, и точку Е3, для которой АЕ3 = 3, и точку Е4, для которой АЕ4 = 4, и точку Еь, для которой АЕЪ = 5, и точку Е6, для которой АЕ6 = 6. На рис. 102 отмечены (приблизительно) соответствующие точки (причем для ориентировки каждая из четвертей единичной окружности разделена черточками на три равные части).

Пример. Пример. Найти на числовой окружности точку, соответствующую числу -7. Решение. Нам нужно, отправляясь из точки А(0) и двигаясь в отрицательном направлении (в направлении по часовой стрелке), пройти по окружности путь длиной 7. Если пройти одну окружность, то получим (приближенно) 6,28, значит, нужно еще пройти (в том же направлении) путь длиной 0,72. Что же это за дуга? Немного меньше половины четверти окружности, т.е. ее длина меньше числа —.

Итак, на числовой окружности, как и на числовой прямой, каждому действительному числу соответствует одна точка (только, разумеется, на прямой ее найти легче, чем на окружности). Но для прямой верно и обратное: каждая точка соответствует единственному числу. Для числовой окружности такое утверждение неверно, выше мы неоднократно убеждались в этом. Для числовой окружности справедливо следующее утверждение. Итак, на числовой окружности, как и на числовой прямой, каждому действительному числу соответствует одна точка (только, разумеется, на прямой ее найти легче, чем на окружности). Но для прямой верно и обратное: каждая точка соответствует единственному числу. Для числовой окружности такое утверждение неверно, выше мы неоднократно убеждались в этом. Для числовой окружности справедливо следующее утверждение. Если точка М числовой окружности соответствует числу I, то она соответствует и числу вида I + 2як, где к — любое целое число (к е 2). В самом деле, 2п — длина числовой (единичной) окружности, а целое число |й| можно рассматривать как количество полных обходов окружности в ту или другую сторону. Если, например, к = 3, то это значит, что мы делаем три обхода окружности в положительном направлении; если к = -7, то это значит, что мы делаем семь (| к | = | -71 = 7) обходов окружности в отрицательном направлении. Но если мы находимся в точке М(1), то, выполнив еще | к | полных обходов окружности, мы снова окажемся в точке М.