Презентация на тему: Производная функции

Закрепление изученного материала по теме «Производная» и ознакомление с её прикладной частью. Закрепление изученного материала по теме «Производная» и ознакомление с её прикладной частью.

1.Исследование функции на монотонность 2.Касательная к графику. 3.Применение производной в математике 4.Применение производной в экономике

Будем считать, что рассматриваемая функция y=f(x) определена и дифференцируема в каждой точке отрезка a ≤ x ≤ b. Будем считать, что рассматриваемая функция y=f(x) определена и дифференцируема в каждой точке отрезка a ≤ x ≤ b. функция f(x) возрастает (или убывает) в промежутке a<x<b, если: производная f '(х) не отрицательна (или не положительна) в промежутке а<х<b, f '(x) ≥ 0 (или f '(x) ≤ 0) Пример. Определить промежутки возрастания и убывания функции: у = х3 — х2 — 8х + 2.

Решение: Чтобы применить признаки возрастания и убывания функции, найдем производную данной функции и определим значения х, при которых она положительна или отрицательна: Решение: Чтобы применить признаки возрастания и убывания функции, найдем производную данной функции и определим значения х, при которых она положительна или отрицательна: у' = Зх2 — 2х — 8. Корни трехчлена: x1= - 4/3, x2=2. Отсюда: у' =3(х+4/3)(х-2). возрастает убывает возрастает + -4/3 - 2 + Ответ: функция возрастает в промежутках - ∞ < x < -4/3 и 2 < x < + ∞ и убывает в промежутке — 4/3 < х <2.

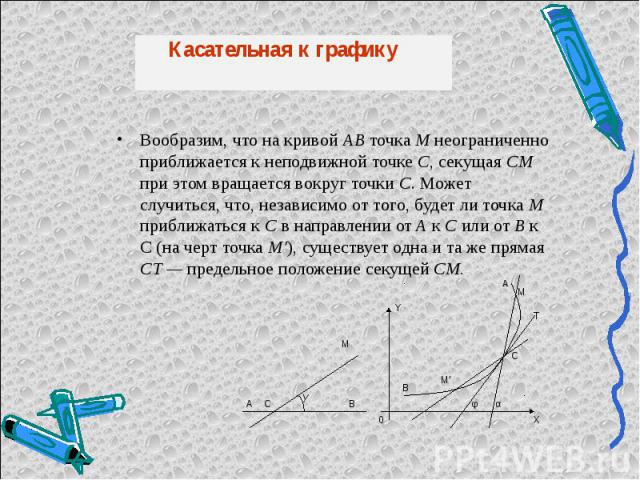
Вообразим, что на кривой АВ точка М неограниченно приближается к неподвижной точке С, секущая СМ при этом вращается вокруг точки С. Может случиться, что, независимо от того, будет ли точка М приближаться к С в направлении от A к С или от В к С (на черт точка M'), существует одна и та же прямая СТ — предельное положение секущей СМ. Вообразим, что на кривой АВ точка М неограниченно приближается к неподвижной точке С, секущая СМ при этом вращается вокруг точки С. Может случиться, что, независимо от того, будет ли точка М приближаться к С в направлении от A к С или от В к С (на черт точка M'), существует одна и та же прямая СТ — предельное положение секущей СМ.

Производная в математике показывает числовое выражение степени изменений величины, находящейся в одной и тоже точке, под влиянием различных условий. Производная в математике показывает числовое выражение степени изменений величины, находящейся в одной и тоже точке, под влиянием различных условий. Формула производной встречается нам ещё в 15 веке. Великий итальянский математик Тартальи, рассматривая и развивая вопрос - на сколько зависит дальность полёта снаряда от наклона орудия - применяет её в своих трудах. Формула производной часто встречается в работах известных математиков 17 века. Её применяют Ньютон и Лейбниц. Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Затем производная и различные изложения с её применением стали встречаться в работах Декарта, французского математика Роберваля и англичанина Грегори. Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лангранж и др.

“Музыка может возвышать или умиротворять душу, “Музыка может возвышать или умиротворять душу, Живопись – радовать глаз, Поэзия – пробуждать чувства, Философия – удовлетворять потребности разума, Инженерное дело – совершенствовать материальную сторону жизни людей, А математика способна достичь всех этих целей”.