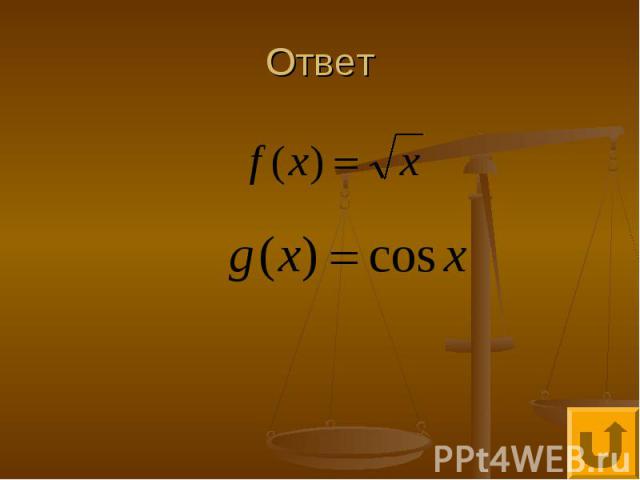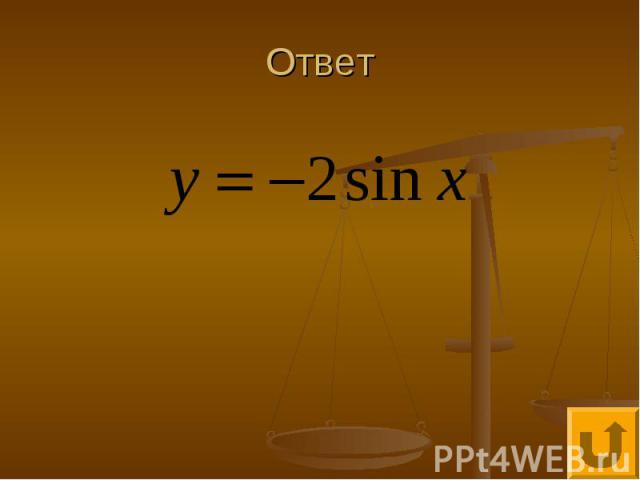Презентация на тему: Своя игра по теме «Тригонометрия»

Обобщающий урок-викторина «Своя игра» по теме «Тригонометрия» МОУ Челно-Вершинская СОШ (ОЦ) Самарской области Составила: Телегова Т.П. – учитель математики

Темы игры История тригонометрии как науки Прямоугольный треугольник Углы и их измерение Вычисления Расскажи мне, расскажи Формулы Исследование тригонометрических функций Проще простого Термины Решаем уравнения и неравенства Числовая окружность Преданья старины глубокой

1 тур

История тригонометрии-20 Именно к этому периоду истории относится зарождение тригонометрии

Ответ Зарождение тригонометрии относится к глубокой древности

История тригонометрии-40 Постепенно в геометрии и астрономии установили эти понятия. По существу, ими оперировали еще древние математики, рассматривая отношение отрезков в треугольниках и окружностях

Ответ Понятия синуса, косинуса и тангенса угла

История тригонометрии-60 Этот древнегреческий астроном, живший во II веке до нашей эры, считается одним из основоположников тригонометрии. Он же является автором первых тригонометрических таблиц.

Ответ Гиппарх

История тригонометрии-80 Важный вклад в развитие тригонометрии были внесены математиками этой страны в период V-XII в.в. н.э. Им были известны соотношения, которые в современных обозначениях пишутся так:

Ответ Индия

История тригонометрии-100 В России первые тригонометрические таблицы были изданы в 1703 году при участии именно этого ученого.

Ответ Л.Ф.Магницкого

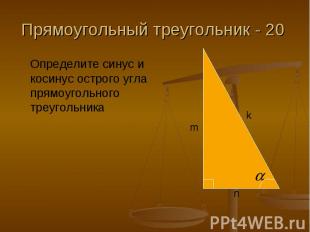
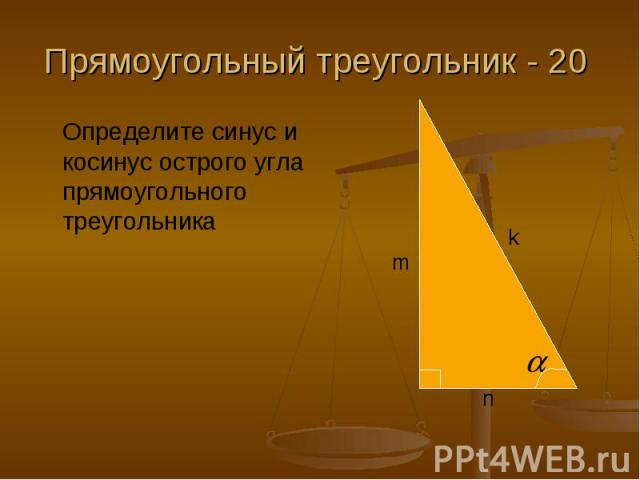
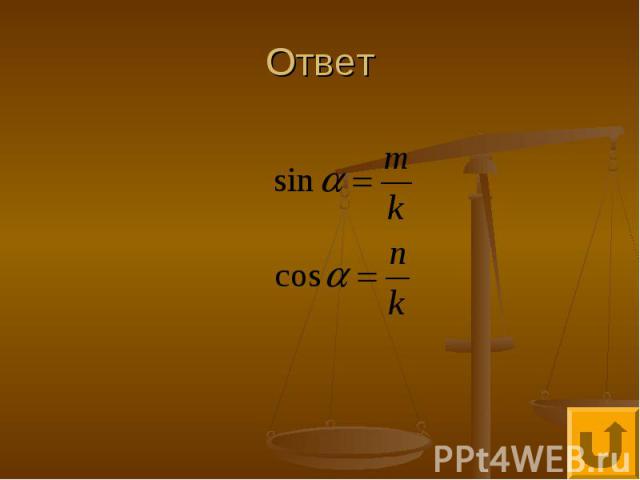
Прямоугольный треугольник - 20 Определите синус и косинус острого угла прямоугольного треугольника

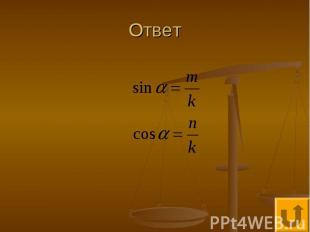
Ответ

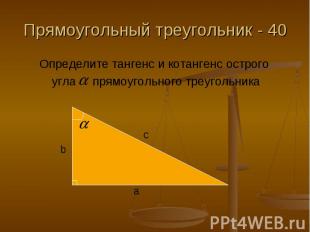
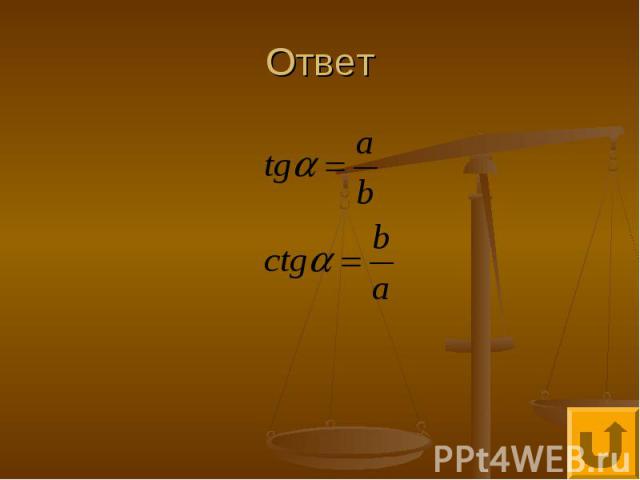
Прямоугольный треугольник - 40 Определите тангенс и котангенс острого угла прямоугольного треугольника

Ответ

Прямоугольный треугольник - 60 Может ли синус угла быть равным ¾ см?

Ответ Нет, так как синус – есть отношение – число отвлеченное, а не именованное.

Прямоугольный треугольник - 80 Даны отрезки a и b. Как построить отрезок ?

Ответ Формула выражает гипотенузу прямоугольного треугольника, у которого катеты a и b.

Прямоугольный треугольник - 100 Один из углов прямоугольного треугольника равен среднему арифметическому двух других его углов. Найдите его катеты, если гипотенуза равна с.

Ответ и

Углы и их измерение - 20 Величина угла выражена в градусах, выразите ее в радианах.

Ответ

Углы и их измерение - 40 Именно в этой четверти лежит этот угол - 830°

Ответ III четверть

Углы и их измерение - 60 Выразим величину угла в радианах, если

Ответ Так как развернутый угол содержит 180° или радиан, то радиан. Поэтому радиан.

Углы и их измерение - 80 Выразим величину угла в градусах, если радиан.

Ответ Так как развернутый угол содержит радиан, или 180°, то Поэтому

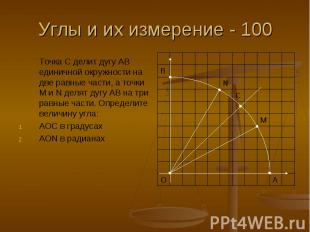
Углы и их измерение - 100 Точка С делит дугу АВ единичной окружности на две равные части, а точки М и N делят дугу АВ на три равные части. Определите величину угла: АОС в градусах АОN в радианах

Ответ 45° .

Вычисления - 20

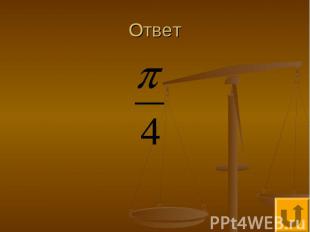
Ответ

Вычисления - 40

Ответ Не существует

Вычисления - 60 Вычислить cos ,если

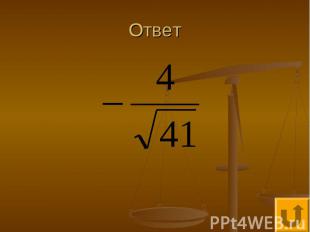
Ответ

Вычисления - 80 если tg =4

Ответ Так как tg =4, то cos ≠0. Разделим числитель и знаменатель дроби на cos : Ответ:

Вычисления -100

Ответ Преобразуем sin0,6 sin0,6 =sin(0,5 +0,1 )=cos0,1 Так как 0,1 Є [0; ], то arccos(sin0,6 )=arccos(cos0,1 )=0,1 Ответ: 0,1

2 тур

Расскажи мне, расскажи - 50 Как располагаются графики функций и относительно графика функции

Ответ График функции получается из графика функции путем его растягивания в 2 раза вдоль оси Оу. График функции получается из графика функции путем его сжатия в 2 раза вдоль оси Ох.

Расскажи мне, расскажи - 100 Графиком функции является

Ответ Прямая

Расскажи мне, расскажи - 150 Расскажите как построить график функции

Ответ Нужно применить тождество , которое справедливо в естественной области определения. Графиком функции является отрезок прямой, заданный уравнением у=х, при

Расскажи мне, расскажи - 200 Графиком функции служит

Ответ Отрезок прямой , соответствующий значениям

Расскажи мне, расскажи - 250 Существуют функции, график которых изобразить невозможно. Такой, например, является

Ответ Функция Дирихле, определенная следующим образом

Исследование тригонометрических функций - 50 Именно для этих действительных чисел определена функция

Ответ Для всех действительных , кроме

Исследование тригонометрических функций - 100 Найдите множество значений функции

Ответ [-3;3]

Исследование тригонометрических функций - 150 Если график функции , заданной на промежутке, есть непрерывная линия, полученная непрерывным движением карандаша без отрыва его острия от бумаги, то эту функцию называют

Ответ Непрерывной на этом промежутке

Исследование тригонометрических функций - 200 С помощью этих основных элементарных функций и задана сложная функция

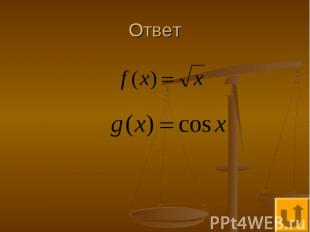
Ответ

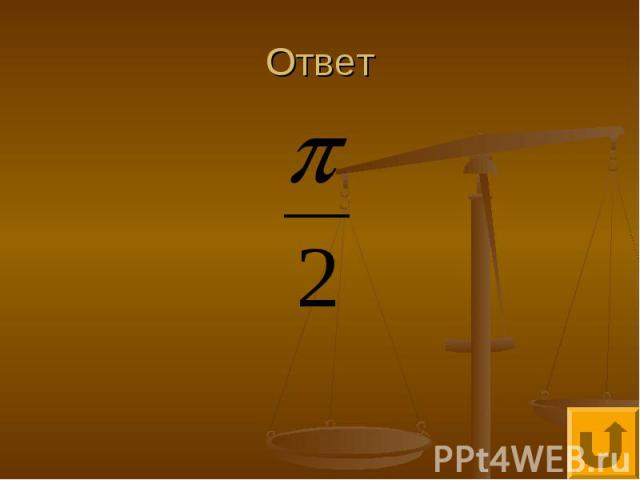
Исследование тригонометрических функций - 250 Наименьший положительный период функции равен

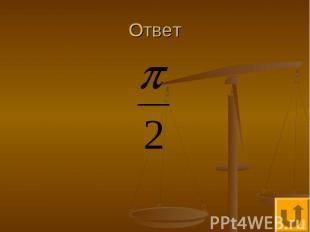
Ответ

Формулы - 50 Значение выражения равно

Ответ -0,5

Формулы -100 Значение выражения равно

Ответ 0,5

Формулы - 150 Найдите значение выражения

Ответ 0

Формулы - 200 Найдите значение выражения

Ответ 1

Формулы - 250 Значение выражения равно

Ответ 0,5

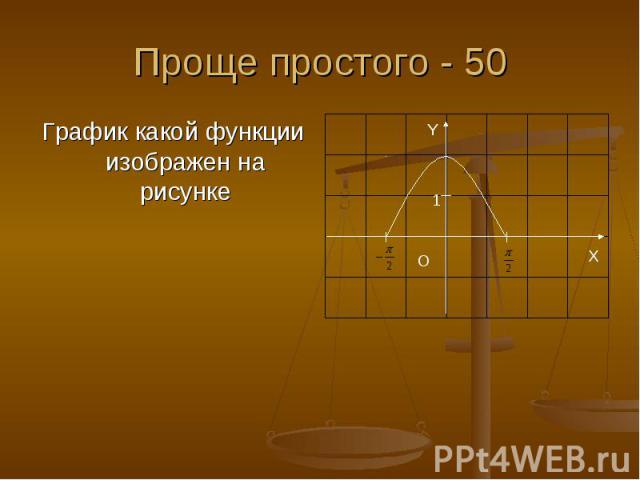
Проще простого - 50 График какой функции изображен на рисунке

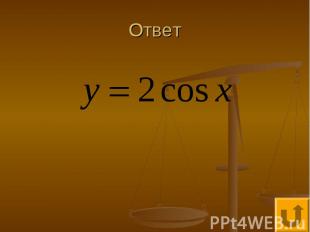
Ответ

Проще простого - 100 График какой функции изображен на рисунке

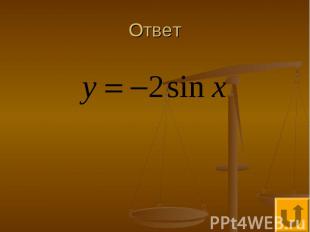
Ответ

Проще простого - 150 Укажите множество значений функции

Ответ

Проще простого - 200 Укажите множество значений функции

Ответ

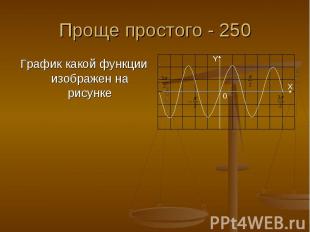
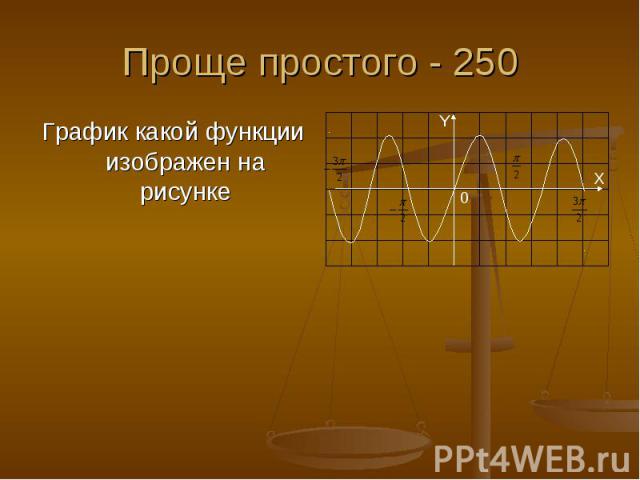
Проще простого - 250 График какой функции изображен на рисунке

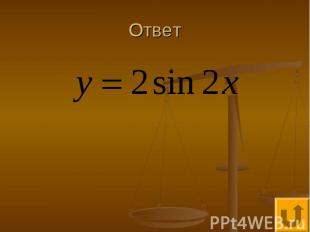
Ответ

3 тур

Преданья старины глубокой - 100 В древнем Египте заметили, что если на веревке завязать узелки на равном расстоянии друг от друга, и натянуть веревку так, чтобы говоря современным языком, получался треугольник со сторонами 3; 4 и 5, то угол лежащий против наибольшей стороны окажется прямым. С тех пор именно так называется треугольник со сторонами 3; 4 и 5

Ответ Египетский

Преданья старины глубокой - 200 Венцом развития астрономии и тригонометрии в Древней Греции считается работа «Большое математическое построение астрономии в 13 книгах» (Альмагест) этого знаменитого астронома.

Ответ Клавдий Птоломей (II в н.э.)

Преданья старины глубокой - 300 В Древнем Египте существовали люди специальной профессии, которых называли ГАРПЕДОНАПТЫ. С них начиналось любое строительство. Назовите предмет, без которого эти люди не выходили на работу.

Ответ ГАРПЕДОНАПТЫ – натягиватели веревки. С помощью веревки ровно в линию выкладывали кирпичи или камни. Еще веревка нужна для того, чтобы получить прямой угол.

Преданья старины глубокой - 400 Впервые они были введены в X в. персидским математиком Абу-ль-Вефой в связи с решением задачи об определении длины тени. А потом заново открыты в XIV в. сначала английским ученым Т. Брадвардином, а позднее немецким математиком, астрономом Региомонтаном (1467г.)

Ответ Тангенсы

Преданья старины глубокой - 500 Легенда гласит, что Фалес (философ и математик) привел в изумление египетского царя Амазиса, измерив высоту одной из пирамид по величине отбрасываемой ею тени. В чем заключалась догадка Фалеса?

Ответ Догадка Фалеса заключалась в том, что в течении дня бывает момент, когда длина тени каждого предмета равна высоте самого этого предмета. Он дождался момента, когда длина его тени стала равна его росту, и тогда, измерив тень пирамиды, вычислил её высоту.

Числовая окружность - 100 Все углы , для которых составляют серию углов

Ответ Все такие углы составляют серию углов

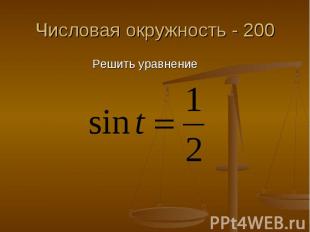
Числовая окружность - 200 Решить уравнение

Ответ Учтем, что - ордината точки М(t) числовой окружности. Значит, нужно найти на числовой окружности точки с ординатой и записать, каким числам t они соответствуют.

Числовая окружность - 300 В трудах этого великого ученого, члена Российской академии наук, тригонометрия получила современный вид. Он начал рассматривать значения тригонометрических функций как числа-величины тригонометрических линий в круге, радиус которого принят за единицу. Он дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из основных. Именно в его трудах впервые встречаются записи

Ответ Леонард Эйлер (1707-1783)

Числовая окружность - 400 Решить неравенство

Ответ Учтем, что - это ордината точки М(t) числовой окружности. Значит, нужно найти на числовой окружности точки с ординатой и записать, каким числам они соответствуют

Числовая окружность - 500 Решить неравенство

Ответ

Решаем уравнения и неравенства - 100 Решите устно уравнение

Ответ 0

Решаем уравнения и неравенства - 200 Решить уравнение

Ответ

Решаем уравнения и неравенства - 300 При решении этого неравенства используется

Ответ Введение вспомогательного угла

Решаем уравнения и неравенства - 400 Уравнение удобно решать при помощи замены

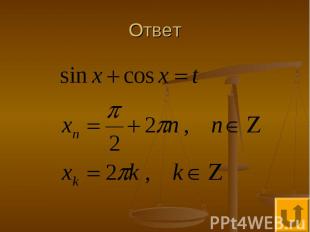
Ответ

Решаем уравнения и неравенства - 500 Назовите четыре типа уравнений, содержащие обратные тригонометрические функции

Ответ простейшие; сводимые к алгебраическим; решаемые с использованием свойств функций; уравнения, решение которых основано на переходе к следствию (применение одной и той же тригонометрической функции к обеим частям уравнения)

Термины - 100 Этот термин буквально означает «тетива лука», «струна»

Ответ Хорда

Термины - 200 Этот термин означает «натянутая»

Ответ Гипотенуза

Термины - 300 Этот термин состоит из двух греческих слов: «тригоном», что означает «треугольник» и «метрейн», что означает «измерять»

Ответ Тригонометрия

Термины - 400 Именно это означает древний термин «катет»

Ответ Отвес

Термины - 500 Это название появилось в 1583г. Переводится с латинского, как «касающийся»

Ответ Тангенс

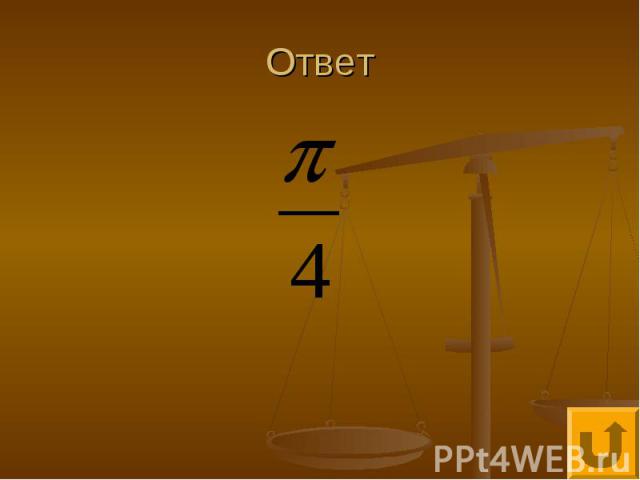
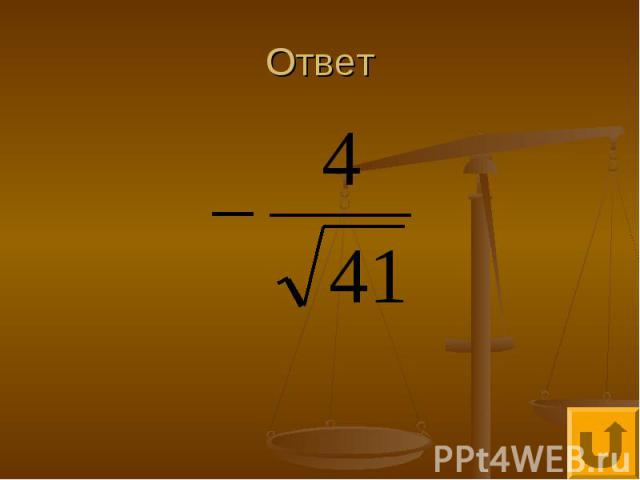
Финал Определить все , при каждом из которых неравенство имеет хотя бы одно решение

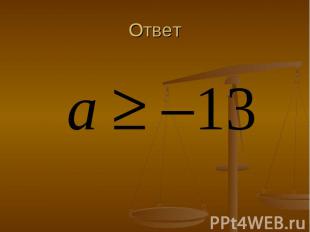
Ответ