Презентация на тему: Тригонометрия

ТригонометрияАвтор: учитель математики Комлякова Ксения ГеннадьевнаГБОУ Гимназия №105, г. Санкт-Петербург

«Приобретать знания – храбрость, приумножать их – мудрость, а умело применять – великое искусство»(восточная мудрость)

I. Простейшие тригонометрические уравнения.
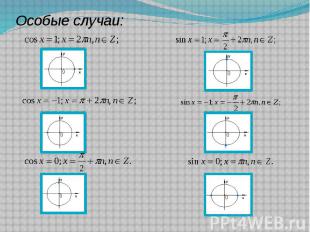
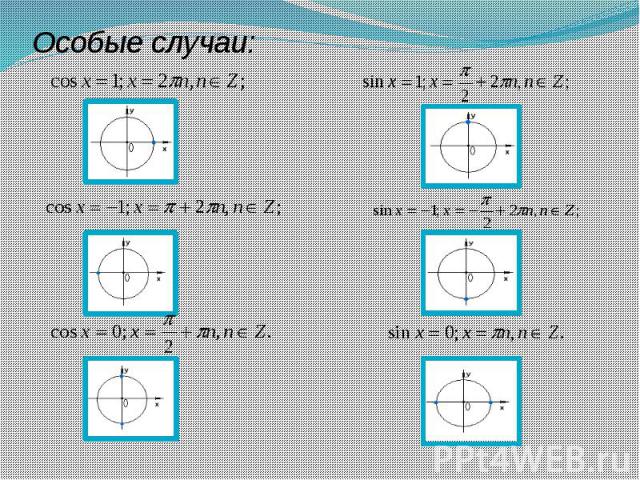
Особые случаи:

Уравнения вида Нужно помнить, что при

Укажите общую формулу, по которой находятся все корни уравнения

Типы тригонометрических уравнений

Примеры решения тригонометрических уравнений

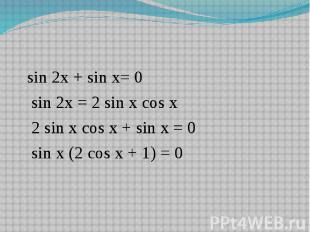
sin 2x + sin x= 0 sin 2x = 2 sin x cos x 2 sin x cos x + sin x = 0 sin x (2 cos x + 1) = 0

4 tg x – 3 ctg x = 1 ctg x = 1/ tg x


Один из способов решения такого уравнения состоит в том, что левую часть уравнения можно преобразовать по формуле:
![2cos3х + 4 sin(х/2) = 7Укажите число корней уравнения на промежутке [0; 2π]:sinх 2cos3х + 4 sin(х/2) = 7Укажите число корней уравнения на промежутке [0; 2π]:sinх](https://fs1.ppt4web.ru/images/4134/62544/310/img13.jpg)
2cos3х + 4 sin(х/2) = 7Укажите число корней уравнения на промежутке [0; 2π]:sinх = ?

Для решения задач повышенной сложности в алгебре используются нестандартные методы решения. Один из таких методов – метод МАЖОРАНТ. Уметь решать задачи методом мажорант важно для более глубинного познания математики. Очень удобно применять метод МАЖОРАНТ при решении нестанадартных уравнений, в левой и правой частях которых, находятся функции, имеющие различную природу.Метод МАЖОРАНТ часто называют методом математической оценки или методом «mini-max».

Термин «мажоранта» происходит от французского слова «majorante», от «majorer» — объявлять большим.Мажорантой функции f(х) на множестве Р называется такое число М, что либо f(х) ≤ М для всех х є Р, либо f(х) ≥ М для всех х є Р. Многие известные нам функции имеют мажоранты.
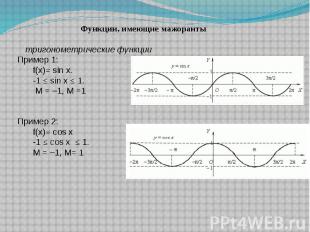
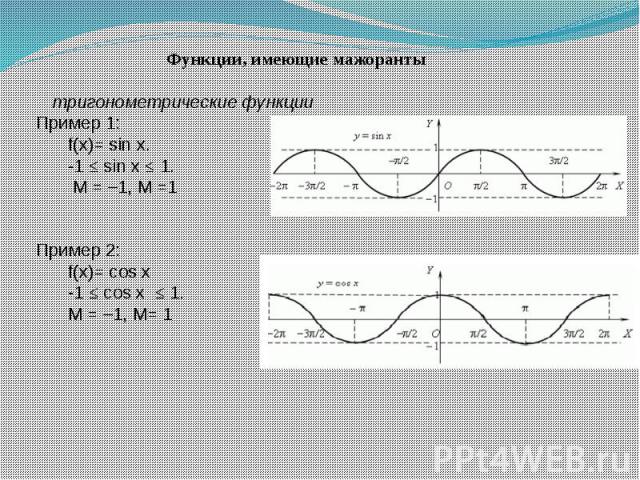
Функции, имеющие мажорантытригонометрические функцииПример 1: f(x)= sin x.-1 ≤ sin x ≤ 1. М = –1, М =1 Пример 2: f(x)= cos x-1 ≤ cos x ≤ 1. М = –1, М= 1
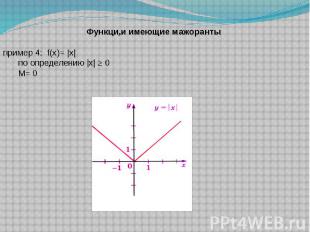
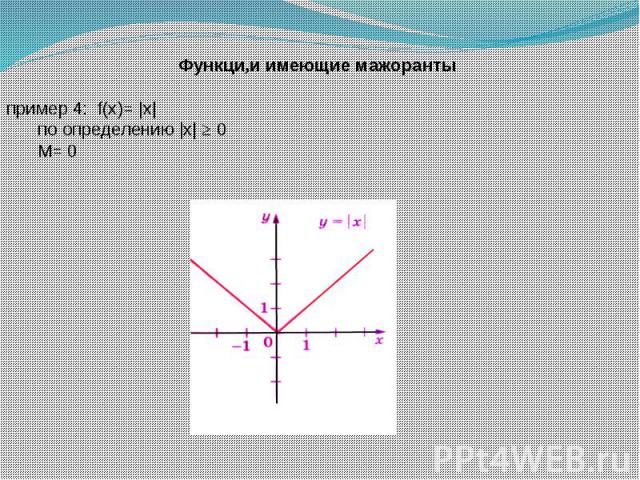
Функци,и имеющие мажоранты пример 4: f(x)= |x| по определению |x| ≥ 0М= 0
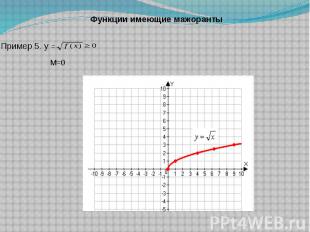
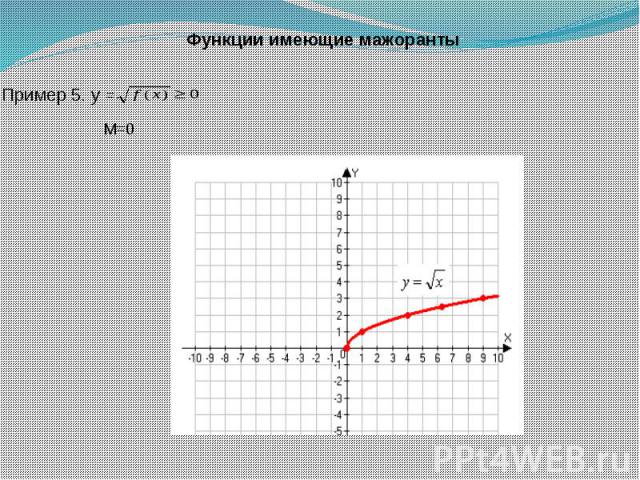
Функции имеющие мажоранты

2. Метод мажорантПусть мы имеем уравнение и существует такое число М, что для любого Х из области определения функций f(x) и g(x) Имеем: Тогда уравнение эквивалентно системе

Оценим левую и правую части уравнения: Равенство будет выполняться, если обе части = 4.

Решим первое уравнение системы: Проверим, является ли найденное число корнем второго уравнения системы:

«Уравнение – это золотой ключ, открывающий все математические сезамы»(С. Коваль)










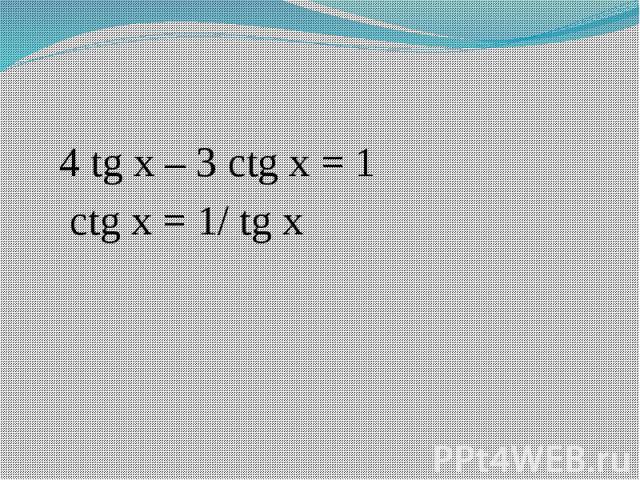
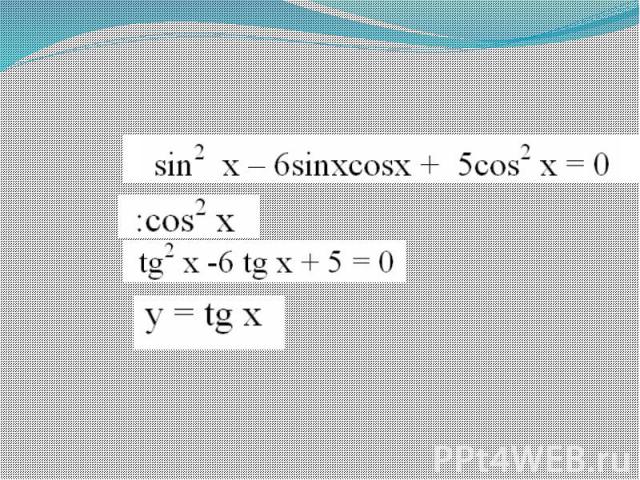

![2cos3х + 4 sin(х/2) = 7Укажите число корней уравнения на промежутке [0; 2π]:sinх = ? 2cos3х + 4 sin(х/2) = 7Укажите число корней уравнения на промежутке [0; 2π]:sinх = ?](https://fs1.ppt4web.ru/images/4134/62544/640/img13.jpg)