Презентация на тему: Предмет стереометрия. Аксиомы стереометрии

Предмет стереометрия.Аксиомы стереометрии.Автор: учитель математики Комлякова Ксения ГеннадьевнаГБОУ Гимназия №105, г. Санкт-Петербург

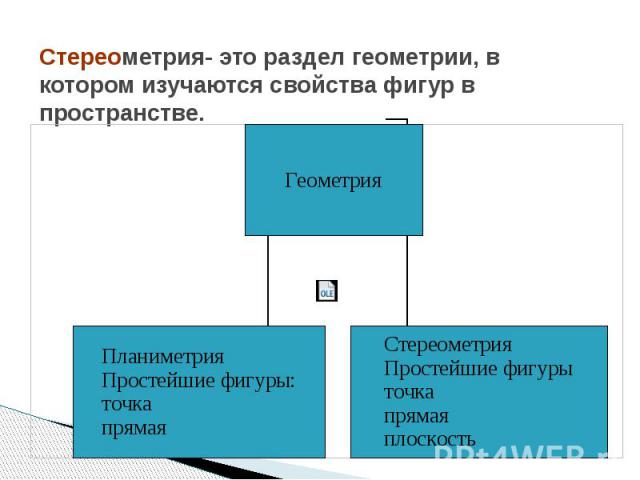
Стереометрия- это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Геометрия возникла из практических нужд человека

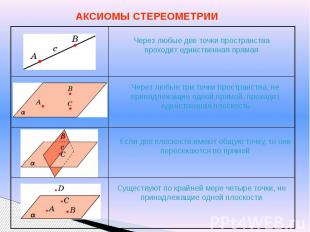
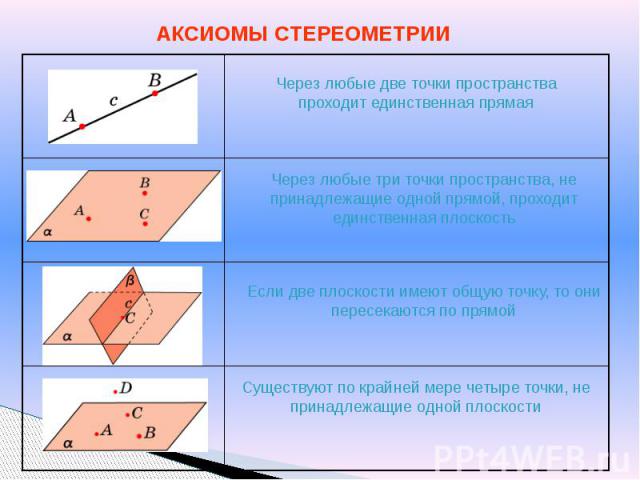
АКСИОМЫ СТЕРЕОМЕТРИИ

ВОПРОС 1 Сколько прямых проходит через две точки пространства? Ответ: Одна.

ВОПРОС 2Сколько плоскостей проходит через три точки пространства? Ответ: Одна, если три точки не принадлежат одной прямой; бесконечно много в противном случае.

ВОПРОС 3 Сколько общих точек могут иметь две плоскости? Ответ: Ни одной, или бесконечно много.

ВОПРОС 4 Верно ли утверждение, что всякие: а) три точки; б) четыре точки пространства принадлежат одной плоскости? Ответ: а) Да; б) нет.

ВОПРОС 5 Верно ли, что если окружность имеет с плоскостью две общие точки, то окружность лежит в этой плоскости? Ответ: Нет.

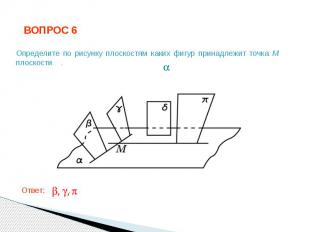
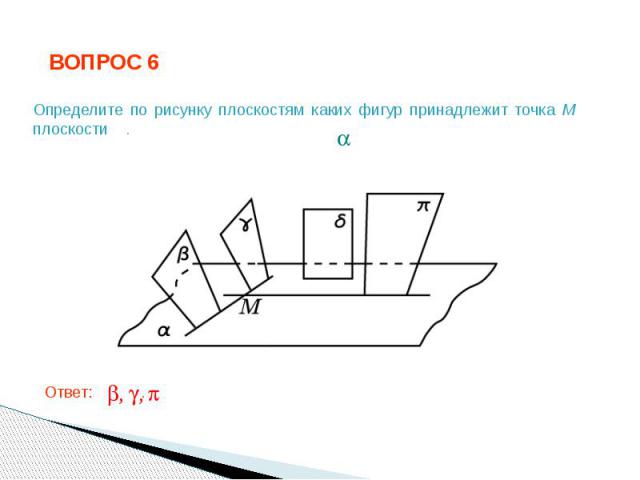
ВОПРОС 6 Определите по рисунку плоскостям каких фигур принадлежит точка M плоскости . Ответ: .

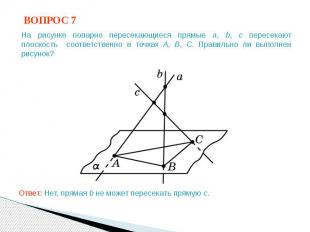
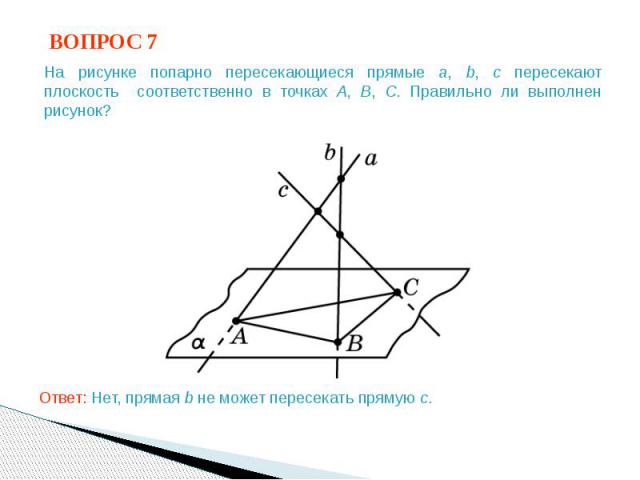
ВОПРОС 7 На рисунке попарно пересекающиеся прямые a, b, c пересекают плоскость соответственно в точках A, B, C. Правильно ли выполнен рисунок? Ответ: Нет, прямая b не может пересекать прямую c.

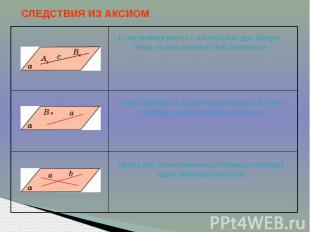
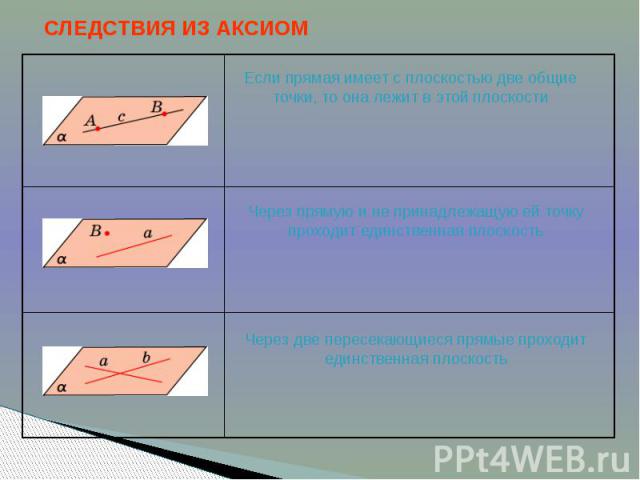
СЛЕДСТВИЯ ИЗ АКСИОМ

Упражнение 1 Четыре точки не принадлежат одной плоскости. Могут ли три из них принадлежать одной прямой? Ответ: Нет.

Упражнение 2 Три вершины параллелограмма принадлежат некоторой плоскости. Верно ли утверждение о том, что и четвёртая вершина этого параллелограмма принадлежит той же плоскости? Ответ: Да.

Упражнение 3 Две вершины и точка пересечения диагоналей параллелограмма принадлежат одной плоскости. Верно ли утверждение о том, что и две другие вершины параллелограмма принадлежат этой плоскости? Ответ: Да.

Упражнение 4 Могут ли вершины замкнутой ломаной, состоящей из трёх звеньев, не принадлежать одной плоскости? Ответ: Нет.

Упражнение 5 Могут ли вершины замкнутой ломаной, состоящей из четырёх звеньев, не принадлежать одной плоскости? Ответ: Да.

Упражнение 6 Верно ли, что через любые две прямые проходит плоскость? Ответ: Нет.

Упражнение 7Прямые a, b, c попарно пересекаются. Верно ли, что они лежат в одной плоскости? Ответ: Нет.

Упражнение 8 Верно ли, что любая прямая, пересекающая каждую из двух данных пересекающихся прямых, лежит в плоскости этих прямых? Ответ: Нет.

Упражнение 9 Прямые a и b пересекаются в точке C. Через прямую a проходит плоскость , через прямую b – плоскость , отличная от . Как проходит линия пересечения этих плоскостей? Ответ: Через точку C.

Упражнение 10 Верно ли, что через любые две прямые проходит плоскость? Ответ: Нет.

Упражнение 11 Верно ли, что через три пересекающиеся прямые проходит плоскость? Ответ: Нет.

Упражнение 12 Сколько плоскостей можно провести через четыре точки? Ответ: Или одну, или ни одной.

Упражнение 13 Сколько плоскостей можно провести через различные тройки из пяти точек, никакие четыре из которых не принадлежат одной плоскости? Ответ: 10.

Упражнение 14 На сколько частей делят пространство три плоскости, имеющие одну общую точку? Ответ: 8.

Упражнение 15 На какое наибольшее число частей могут делить пространство; а) одна плоскость; б) две плоскости; в) три плоскости; в) четыре плоскости? Ответ: а) 2;