Презентация на тему: Площадь треугольника 8 класс

МОУ «ООШ с.Никольское Духовницкого района Саратовской области» Площадь прямоугольника и треугольника Автор: ученика 8 класса Якунина Андрея Руководитель: Бурукина Н.Н. 2011г. 900igr.net

Площадь треугольника Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию
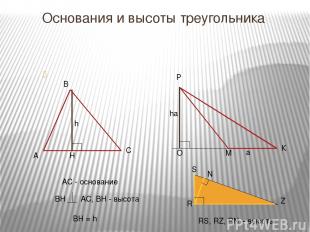
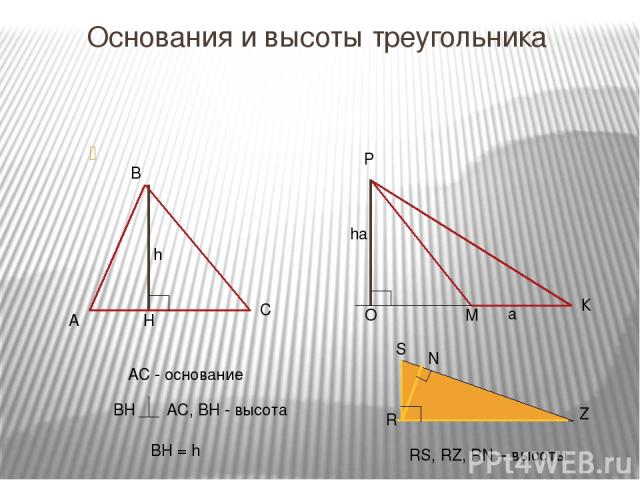
Основания и высоты треугольника АС - основание BH = h RS, RZ, RN – высоты

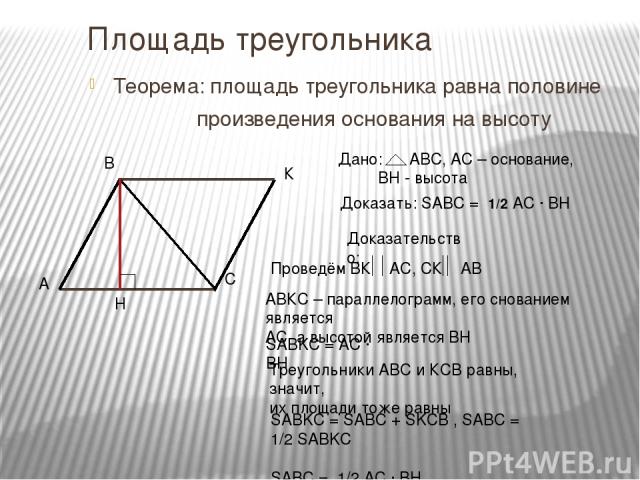
Площадь треугольника Теорема: площадь треугольника равна половине произведения основания на высоту Доказать: SABC = 1/2 AC ∙ BH Доказательство: АВКС – параллелограмм, его снованием является АС, а высотой является ВН SABKC = AC ∙ BH SABKC = SABC + SKCB , SABC = 1/2 SABKC SABC = 1/2 AC ∙ BH Треугольники АВС и КСВ равны, значит, их площади тоже равны К Дано: АВС, АС – основание, ВН - высота Проведём ВК АС, СК АВ
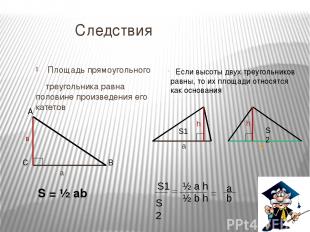
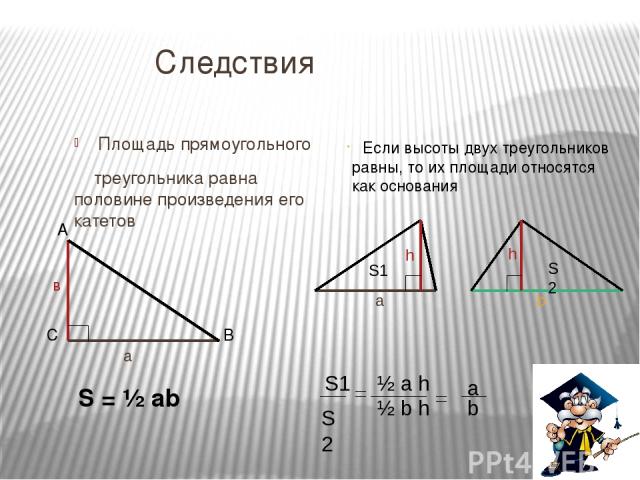
Следствия Площадь прямоугольного треугольника равна половине произведения его катетов S = ½ ab Если высоты двух треугольников равны, то их площади относятся как основания h a S1 h b S2 S1 S2 ½ a h ½ b h a b
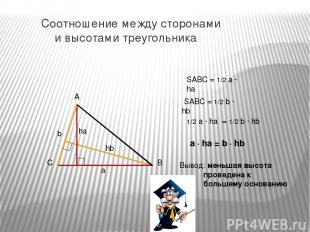
Соотношение между сторонами и высотами треугольника SABC = 1/2 a ∙ ha SABC = 1/2 b ∙ hb 1/2 a ∙ ha = 1/2 b ∙ hb a ∙ ha = b ∙ hb Вывод: меньшая высота проведена к большему основанию

Теорема: если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы. Доказательство: Треугольники АВС и АNC имеют общую высоту СН SABC : SANC = AB : AN, SABC : SANC = AB : MN (1) Треугольники ANC и ANK имеют общую высоту NH1 SANC : SANK = AС: AK, SANC : SANK = АС : MK (2) Дано: АВС и MNK M Перемножив равенства (1) и (2), получим: А В M N K С Наложим MNK на АВС так, чтобы М совпал с А N

Равные многоугольники имеют равные площади

Площадь всего многоугольника равна сумме площадей его частей, на которые он разбит некоторой прямой.

Площадь квадрата равна квадрату длины его стороны, т.е. площадь квадрата со стороной а вычисляется по формуле. а S=а2


Площадь прямоугольника: S=а·b

Литература Интернет Геометрия. 7-9 классы: учеб. Для общеобразоват . учреждений /Л С Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.) – 19- е изд. – М. : Просвещение, 2009. – 384с.