Презентация на тему: Площадь круга

Длина окружности и площадь круга План урока. 1. Вывод формулы длины окружности. 2. Вывод формулы длины дуги окружности. 3.Вывод формулы площади круга. 4. Вывод формулы площади кругового сектора. 900igr.net

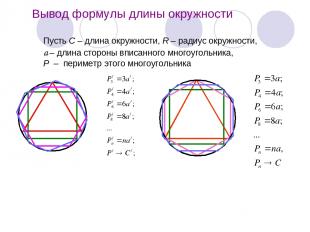
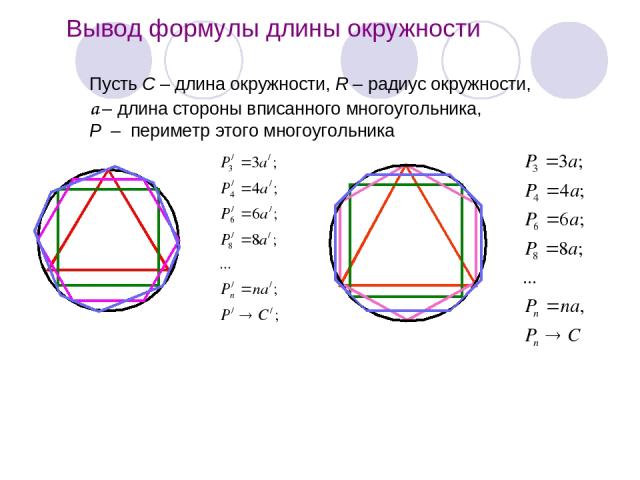
Вывод формулы длины окружности Пусть С – длина окружности, R – радиус окружности, а – длина стороны вписанного многоугольника, Р – периметр этого многоугольника

Т.к а =2Rsin180/n , то Р:Р` =2R:2R`; Т.к Р → С, то при n→ ∞ предел Р:Р`=C:C` Таким образом, С:С`=2R:2R`. Следовательно , С:2R = C`:2R`. С:2R –число постоянное для всех окружностей и его принято обозначать буквой . Из равенства C:2R= , получим формулу для вычисления длины окружности радиуса R: С =2 R. π = 3,14159 (при решении 3; 3,1; 3,14)

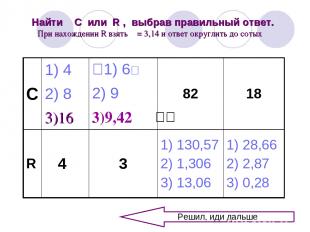
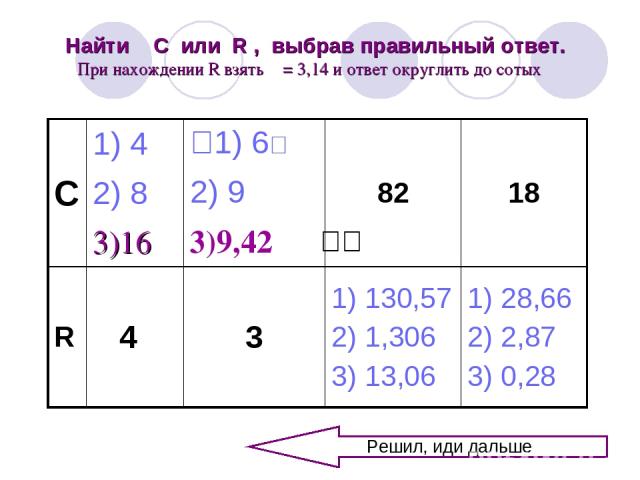
Найти С или R , выбрав правильный ответ. При нахождении R взять π = 3,14 и ответ округлить до сотых Решил, иди дальше

вернуться

вернуться

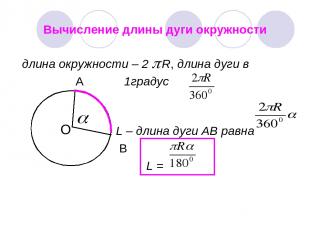
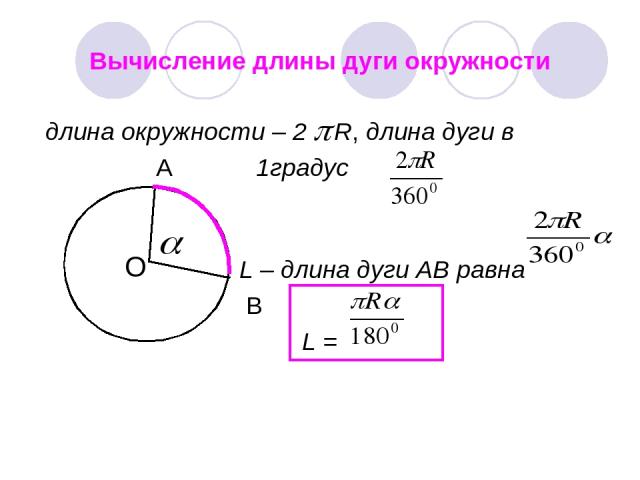
Вычисление длины дуги окружности длина окружности – 2 R, длина дуги в A 1градус L – длина дуги АВ равна B L = О

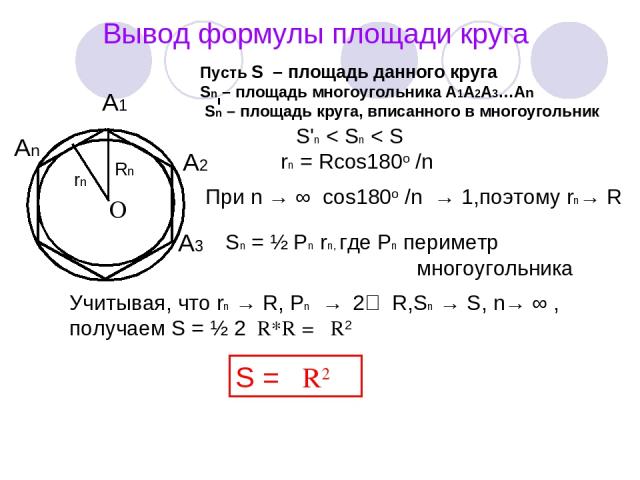
Вывод формулы площади круга А1 А2 А3 Аn O Rn rn Пусть S – площадь данного круга Sn – площадь многоугольника А1А2А3…An Sn – площадь круга, вписанного в многоугольник S'n < Sn < S rn = Rcos180о /n При n → ∞ cos180о /n → 1,поэтому rn→ R Sn = ½ Pn rn, где Pn периметр многоугольника Учитывая, что rn → R, Pn → 2 πR,Sn → S, n→ ∞ , получаем S = ½ 2πR*R = πR2 S = πR2

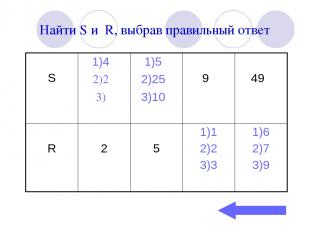
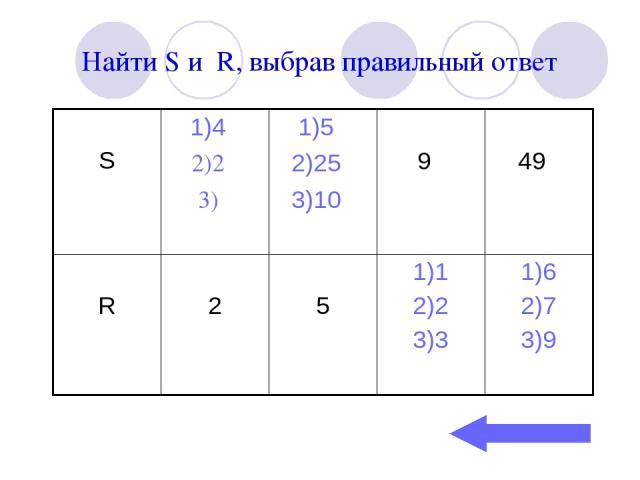
Найти S и R, выбрав правильный ответ

Вывод формулы площади кругового сектора О А В R Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Площадь всего круга – πR2 Площадь кругового сектора, ограниченного дугой в 10 – πR2 /3600 Площадь кругового сектора в α градусов выражается формулой S = πR2α /3600

Выпиши в тетрадь и стрелками укажи соответствие между формулой и её названием С = 2πR площадь круга S = πR2 длина дуги окружности L = πRα / 1800 площадь кругового сектора S = πR2α /3600 длина окружности ПРОВЕРЬ СЕБЯ

Данная презентация предлагается в помощь учителю при объяснении нового материала по теме «Длина окружности и площадь круга» в 9 классе. При подготовке использован материал учебника Геометрия, 7 – 9 , авторы: Л.С.Атанасян, В.Ф.Бутузов и др. М.; Просвещение, 2004 г. Презентация подготовлена учителем математики МОУ «СОШ №4» г. Сосновоборска Красноярского края Евгенией Николаевной Парфёнычевой