Презентация на тему: Площадь трапеций

ГЕОМЕТРИЯ 8 класс Площадь трапеции МОУ СОШ №2 г. Советский Учитель математики Иркашева Татьяна Биктаировна 5klass.net

Проверка домашнего задания №472 Дано: ABC-прямоугольный треугольник S∆ABC=168 см², AB:AC=7:12 Найти: AB и AC РЕШЕНИЕ. S∆ABC=½АС·ВС 168=½7х·12х 168=42х² х=2 АС=14 см, ВС=24 см Ответ: 14 см и 24 см. А B C 7x 12x

Устно Дано: АВСД – параллелограмм АД=10см, АВ=6см, 30º Найти: Sпар А В С Д 10см 6см 30º А .Решение Проведём высоту ВН Треугольник АВН – прямоугольный. В прямоугольном треугольнике катет, лежащий против угла в 30º, равен половине гипотенузы. ВН=6:2=3см Sпар= АД*ВН = 10*3=30см2 Ответ: 30см2

Устно: Дано: ∆ABC, S ∆ABC= 24 см², АС=8см Найти: ВН Решение S∆ABC=½АС·ВН 24 = ½*8*ВН 48 = 8*ВН ВН=6см Ответ: 6см А В С Н В

Трапеция ВС параллельна АД, АВ не параллельна СД МN – средняя линия трапеции MN параллельна АД и СД АС и ВД - диагонали трапеции Если АВ=СД, то трапеция равнобедренная В равнобедренной трапеции углы при основании равны. А= В, В= С А В С Д О основание основание M N
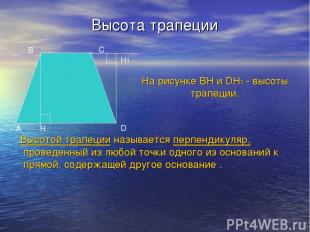
Высота трапеции Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание . A B С D H H1 На рисунке BH и DH1 - высоты трапеции.

Теорема: Площадь трапеции равна произведению полусуммы её оснований на высоту Дано: ABCD-трапеция AD и BC – основания трапеции BH – высота трапеции Доказать: Sтр= 1/2(AD+BC) BH Доказательство: 1. Е – середина основания AD, AE=ED 2. Проведём BE и CE 3. Получаем треугольники: ABE, BEC, CDE По свойству площадей площадь трапеции равна сумме площадей трёх треугольников. SABCD=SABE+SBEC+SCED=1/2AE BH+1/2ED BH+1/2BC BH= =1/2 (AE+ED+BC)BH= ½ (AD+BC) BH A B C D H E

Второй способ доказательства: Доказательство: 1. Сложим две одинаковые трапеции так, чтобы получился параллелограмм Sтр= ½ Sпар = 1/2 (a+b) h Sтр= ½ (a+b)h, где а и b- основания трапеции h – высота трапеции a b a b h

Третий способ доказательства теоремы: а в s=sпар+sтр= =bh+1/2(а-b)h=1/2(a+b)h h a-b

№480б Дано: АВСД – трапеция, АВ и СД – основания трапеции Д=30º, АВ=2см, СД= 10см, ДА=8см Найти: Sтр Решение. 1. Sтр=1/2 (CД+АВ) АН 2. АН находим из прямоугольного ∆АДН. 3. Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы АН=8:2=4см Sтр= ½ (АВ+СД) АН = ½ ( 2+10) 4 = 24 см² Ответ: 24 см² С А Д В H 30 2 8 10

№481 Дано: АВСД – прямоугольная трапеция АВ=ВС=6см, С=135º Найти: Sтр Решение. 1. Проведём СН АД 2. Рассмотрим прямоугольный ∆СНД 3. НСД=135º - 90º = 45º 4. СДН = 90º - 45º = 45º 5. ∆СНД – прямоугольный и равнобедренный. СН=НД=6см АД=АН+НД = 6+6 = 12 см Sтр=1/2 (АД+ВС) АН= ½ (12+6) 6=54 см² Ответ: 54 см² А С В Д 6 6 Н

Домашнее задание: № 480а № 482 пп. 48-53. Найти другие способы доказательства теоремы о площади трапеции.