Презентация на тему: Длина окружности. Площадь круга

Длина окружности.Площадь кругаВыполнила учитель математикилицея №1 г. СемёноваЧечина Ольга Юрьевна

Повторение

Веер имеет форму кругового сектора. Найдите площадь этого сектора и длину дуги, которую образует развернутый веер, если радиус равен 30 см, а градусная мера угла 160°

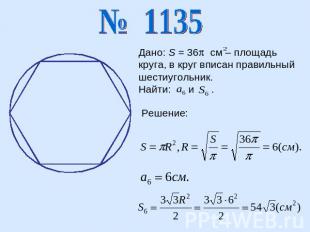
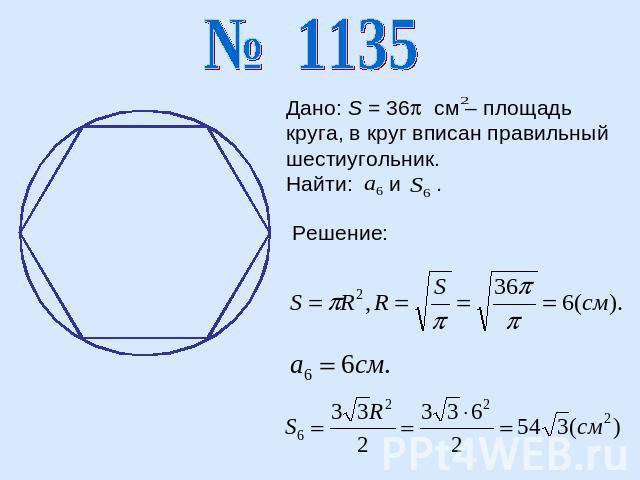
Дано: S = 36 см – площадь круга, в круг вписан правильный шестиугольник.Найти: и .

1. Найдите угол правильного десятиугольника 1) 288° 2) 144° 3) 164° 2. Найдите сторону правильного треугольника, если радиус описанной около него окружности равен 2 м. 1) 2√3 м 2) 2 м 3) 6 м3. Найдите площадь кругового сектора радиуса 4 см, если его центральный угол равен 90°. 1) π см 2) 4π см 3) 8π см

4. Найдите радиус описанной около квадрата окружности, если сторона квадрата равна 6 м. 1) 6√2 м 2) 12 м 3) 3√2 м5. Найдите радиус окружности, вписанной в правильный треугольник, если радиус описанной около него окружности равен 2 м. 1) 1 м 2) 2 м 3) 4 м6. Найдите длину дуги окружности радиуса 6 дм, если её градусная мера равна 120°. 1) 2 π 2) 3 π 3) 4π

№ 1 № 2 № 3 № 4 № 5 № 6 № 1 № 2 № 3 № 4 № 5 № 6 2 1 2 3 1 3

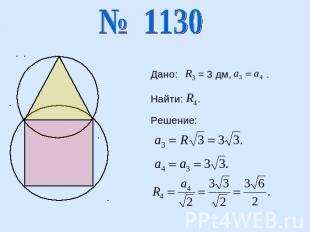
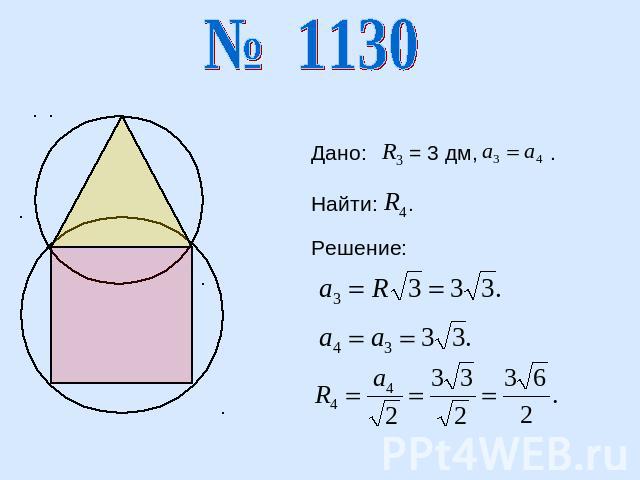
Дано: = 3 дм, .Найти: .

Задачи для домашней работы. Найдите площади секторов, на которые разбивают круг два радиуса длиной 4 м, а угол между ними равен 36°.2. Найдите длины дуг, на которые разбивают окружность два радиуса длиной 6 дм, если угол между ними равен 72°.3. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.4. Периметр квадрата, вписанного в окружность, равен 48 см. Найдите сторону правильного пятиугольника, вписанного в ту же окружность.

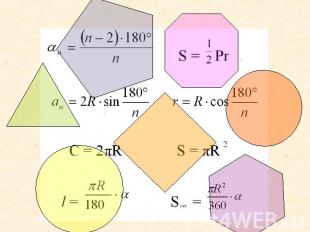
Длина окружности.Площадь круга.

Сформулируйте определение правильного многоугольника.

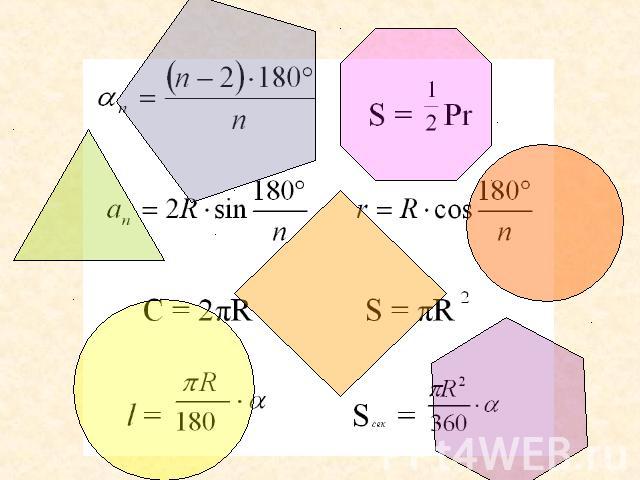
Запишите формулу для нахождения площади сектора.

Какая точка называется центром правильного многоугольника?

Запишите формулу для нахождения длины дуги окружности.

Какое число обозначается буквой π и чему равно его приближенное значение?

Запишите формулу для нахождения площади круга.

Запишите формулу для нахождения длины окружности.

Запишите формулу для нахождения угла правильного многоугольника.

Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.

Периметр квадрата, вписанного в окружность, равен 48 см. Найдите сторону правильного пятиугольника, вписанного в ту же окружность.