Презентация на тему: Алгоритмы построения графиков функции

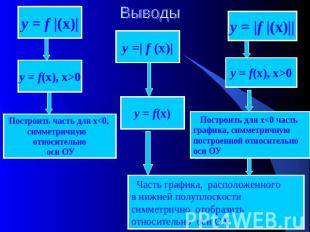
Алгоритмы построения графиков функции

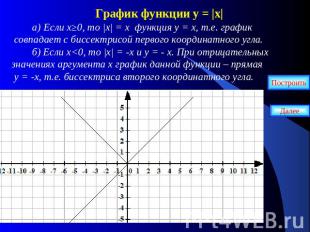
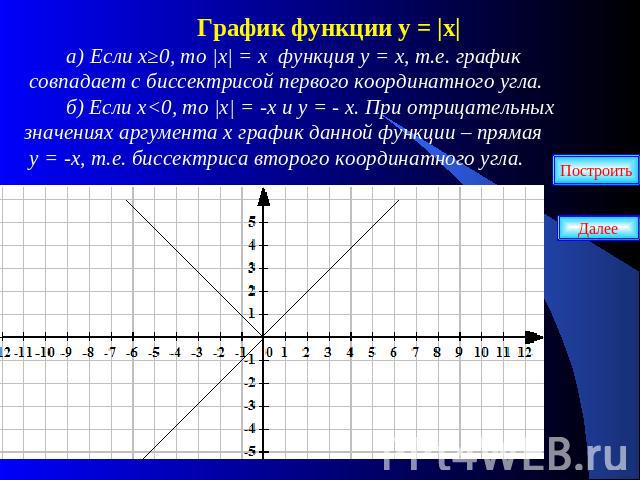
График функции у = |х| а) Если х≥0, то |х| = х функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х<0, то |х| = -х и у = - х. При отрицательных значениях аргумента х график данной функции – прямая у = -х, т.е. биссектриса второго координатного угла.

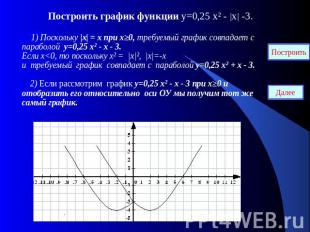
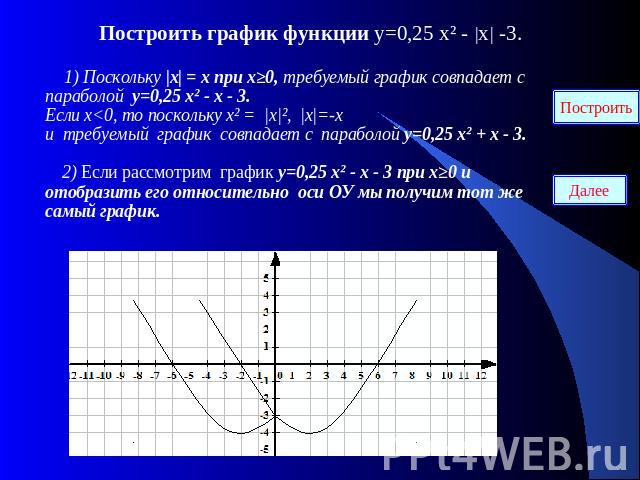
Построить график функции у=0,25 х² - |х| -3. 1) Поскольку |х| = х при х≥0, требуемый график совпадает с параболой у=0,25 х² - х - 3. Если х<0, то поскольку х² = |х|², |х|=-х и требуемый график совпадает с параболой у=0,25 х² + х - 3. 2) Если рассмотрим график у=0,25 х² - х - 3 при х≥0 и отобразить его относительно оси ОУ мы получим тот же самый график.

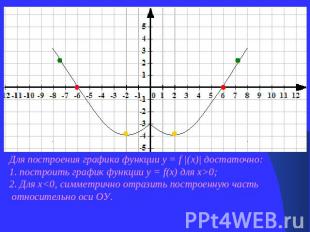
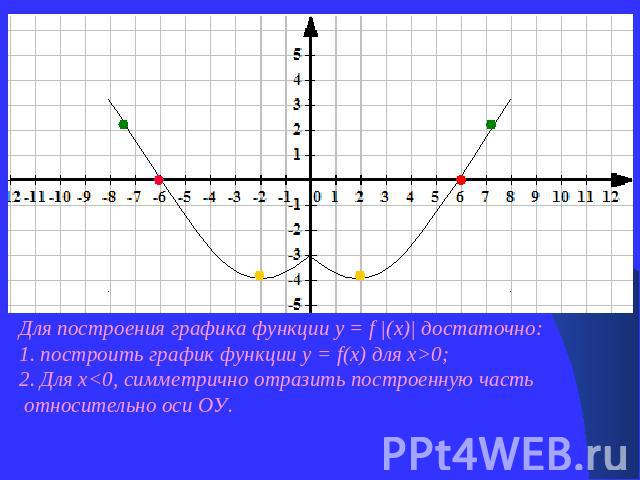
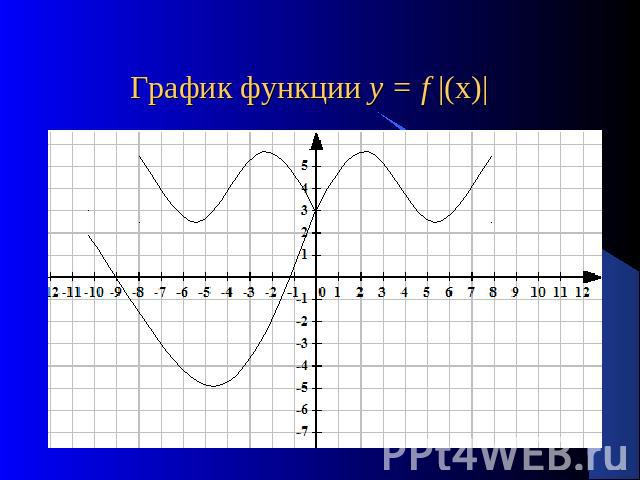
Для построения графика функции у = f |(х)| достаточно: 1. построить график функции у = f(х) для х>0;2. Для х<0, симметрично отразить построенную часть относительно оси ОУ.

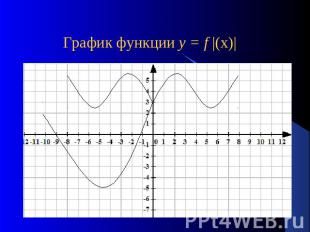
График функции у = f |(х)|

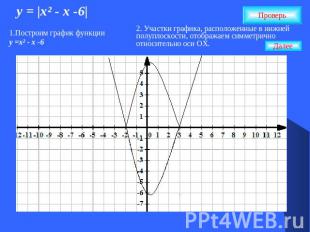
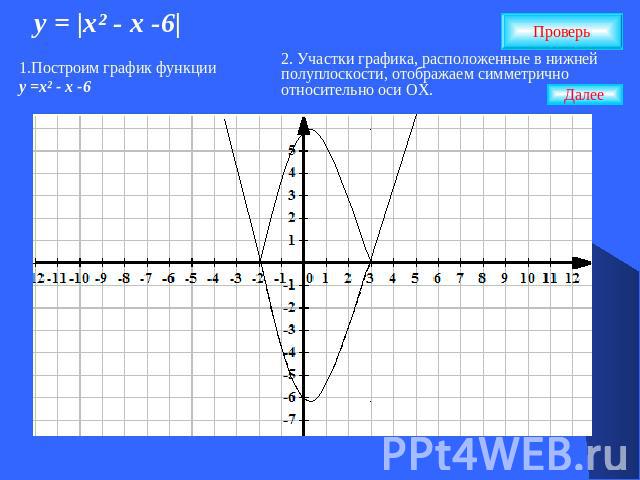
у = |х² - х -6| 1.Построим график функции у =х² - х -6 2. Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.

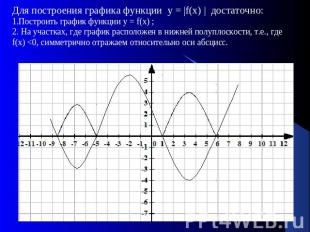
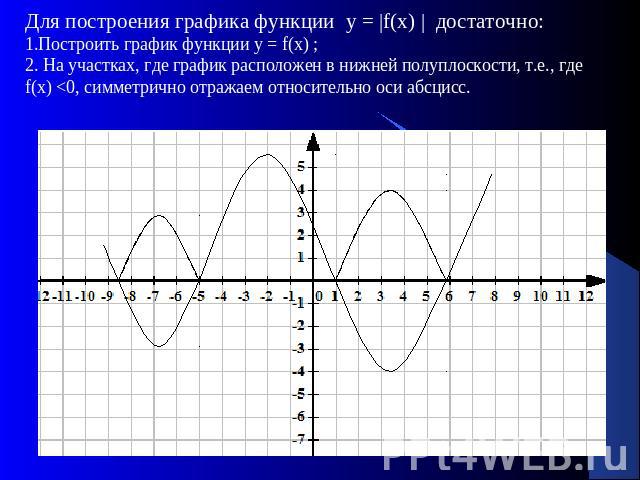
Для построения графика функции у = |f(х) | достаточно:1.Построить график функции у = f(х) ;2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс.

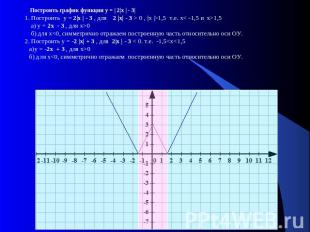
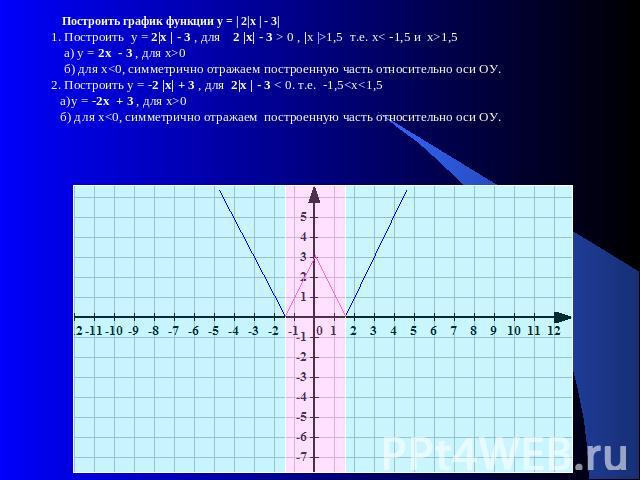
Построить график функции у = | 2|х | - 3|1. Построить у = 2|х | - 3 , для 2 |х| - 3 > 0 , |х |>1,5 т.е. х< -1,5 и х>1,5 а) у = 2х - 3 , для х>0 б) для х<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Построить у = -2 |х| + 3 , для 2|х | - 3 < 0. т.е. -1,5<х<1,5 а)у = -2х + 3 , для х>0 б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

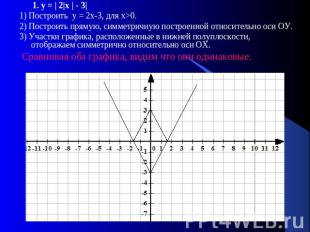
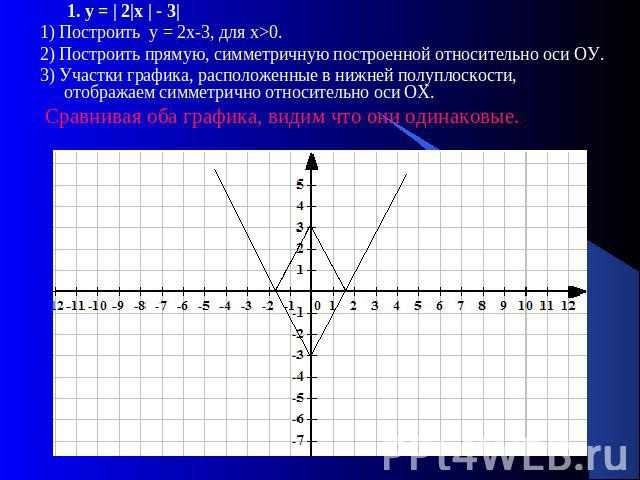
1. у = | 2|х | - 3|1) Построить у = 2х-3, для х>0. 2) Построить прямую, симметричную построенной относительно оси ОУ.3) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ. Сравнивая оба графика, видим что они одинаковые.

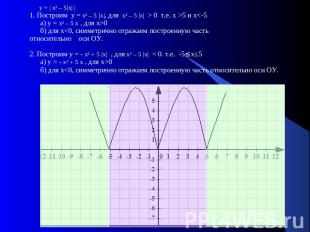
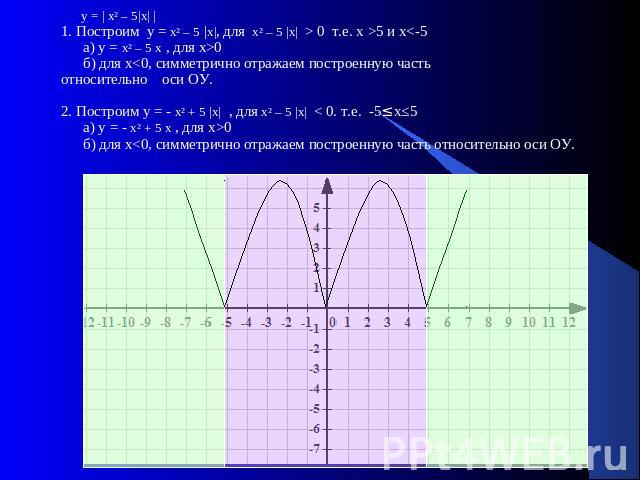
у = | х² – 5|х| |1. Построим у = х² – 5 |х|, для х² – 5 |х| > 0 т.е. х >5 и х<-5 а) у = х² – 5 х , для х>0 б) для х<0, симметрично отражаем построенную частьотносительно оси ОУ. 2. Построим у = - х² + 5 |х| , для х² – 5 |х| < 0. т.е. -5≤х≤5 а) у = - х² + 5 х , для х>0 б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

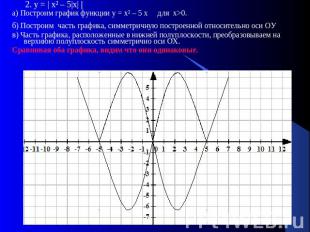
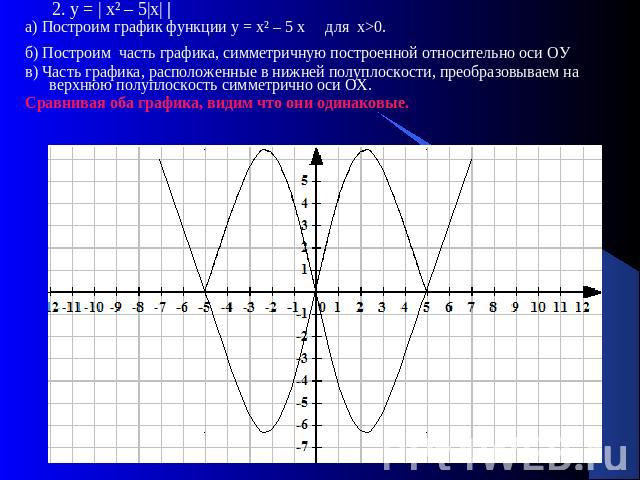
2. у = | х² – 5|х| |а) Построим график функции у = х² – 5 х для х>0.б) Построим часть графика, симметричную построенной относительно оси ОУ в) Часть графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.Сравнивая оба графика, видим что они одинаковые.

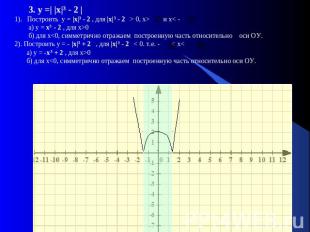
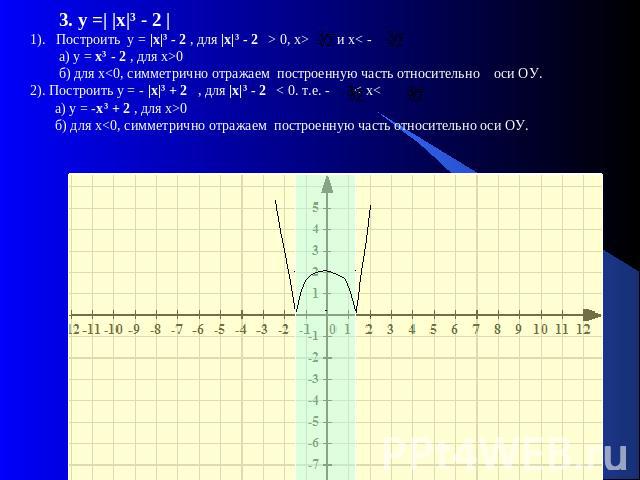
3. у =| |х|³ - 2 |1). Построить у = |х|³ - 2 , для |х|³ - 2 > 0, x> и x< - а) у = х³ - 2 , для х>0 б) для х<0, симметрично отражаем построенную часть относительно оси ОУ. 2). Построить у = - |х|³ + 2 , для |х|³ - 2 < 0. т.е. - < x< а) у = -х³ + 2 , для х>0 б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

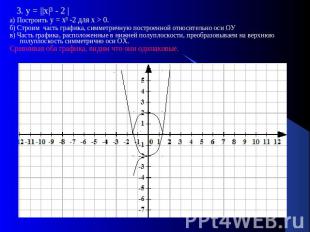
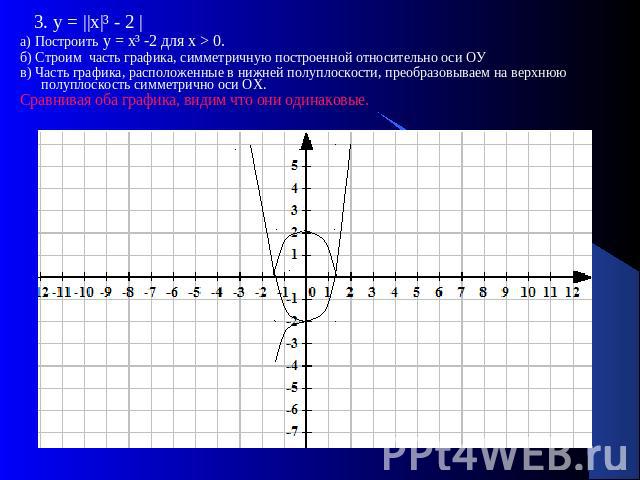
3. у = ||х|³ - 2 |а) Построить у = х³ -2 для х > 0.б) Строим часть графика, симметричную построенной относительно оси ОУв) Часть графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они одинаковые.

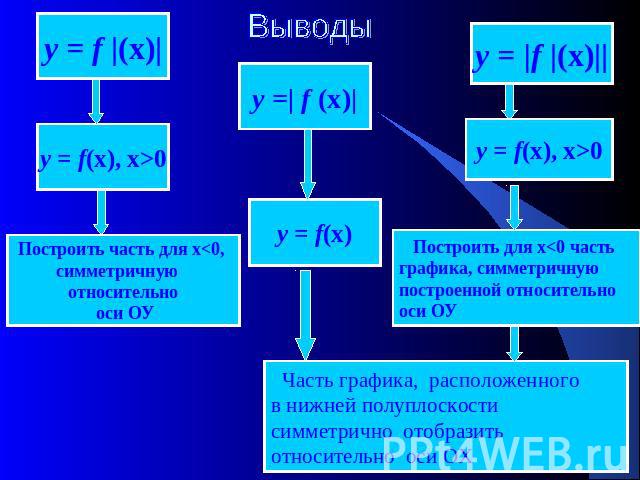
Для построения графика функции у = f |(х)|: 1.Построить график функции у = f(х) для х>0; 2.Построить для х<0 часть графика, симметричную построенной относительно оси ОУ. Для построения графика функции у = | f(х) | 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, строить кривые, симметричные построенным графикам относительно оси абсцисс. Для построения графика функции у = | f |(х)| | 1. Построить график функции у = f(х) для х>0. 2. Строим вторую часть графика, т. е. построенный график симметрично отражаем относительно ОУ 3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.