Презентация на тему: Логарифм. Основные понятия

ЛОГАРИФМОсновные понятия

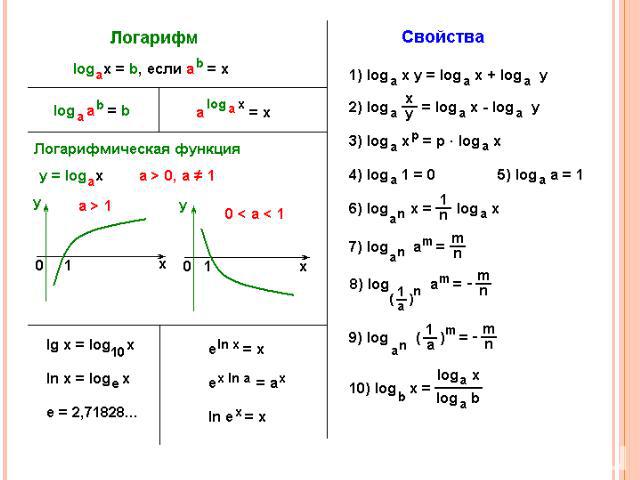
ОПРЕДЕЛЕНИЕЛогарифм числа a по основанию b определяется как показатель степени, в которую надо возвести число b, чтобы получить число a. Обозначение: logba. Из определения следует, что записи logba = x и bx = a эквивалентны.Где b не = 1, a>0, b > 0Пример: log28 = 3, потому что 23 = 8.

ВЕЩЕСТВЕННЫЙ ЛОГАРИФМЛогарифм вещественного числа logba имеет смысл при .Наиболее широкое применение нашли следующие виды логарифмов:Десятичные: основание: число 10.Натуральные: основание: e (число Эйлера).Двоичные: основание: число 2. Они применяются в теории информации и информатике.Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию, например: . Эта функция определена в правой части числовой прямой: x > 0, непрерывна и дифференцируема

НАТУРАЛЬНЫЕ ЛОГАРИФМЫДля производной натурального логарифма справедлива простая формулаПо этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений, исследовании статистических зависимостей (например, распределения простых чисел) и т. п.

Десятичные логарифмы Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:Физика — интенсивность звука (децибелы).Астрономия — шкала яркости звёзд.Химия — активность водородных ионов (pH).Сейсмология — шкала Рихтера.Теория музыки — нотная шкала.

СВОЙСТВА ЛОГАРИФМОВlog   b = 1 ,  так как  b 1 = b .           b                             2)   log   1 = 0 ,  так как  b 0 = 1 .          b3) log   a = a     b b     основное тригонометрическое тождество   

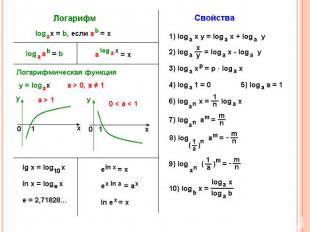
СВОЙСТВА ЛОГАРИФМОВ Логарифм произведения равен сумме логарифмов сомножителей: log ( ab ) = log  a + log  b . 5)  Логарифм частного равен разности логарифмов делимого и делителя:          log ( a / b ) = log  a – log  b . 

Свойства логарифмов6)  Логарифм степени равен произведению показателя степени на логарифм её основания:   Log  ( b k ) = k · log  b .7) Логарифм основания в степени равен произведению степени в минус первой степени на логарифм её основанияLog n b= 1/n log b a a

Презентацию приготовила Кошелева Настя