Презентация на тему: Сумма углов треугольника 2

Закрепить и проверить знания учащихся по теме «Свойства углов, образованных при пересечении двух параллельных прямых третьей» и «Признаки параллельных прямых». Закрепить и проверить знания учащихся по теме «Свойства углов, образованных при пересечении двух параллельных прямых третьей» и «Признаки параллельных прямых». Вывести доказательство свойства углов треугольника. Научить применению этих свойств при решении простейших задач. Способствовать развитию познавательной активности учащихся с помощью исторического материала. Воспитывать навыки аккуратности при построении чертежей.

Повторение и проверка знаний по теме «Параллельные прямые» Повторение и проверка знаний по теме «Параллельные прямые» Устный счет Из истории математики Закрепление изученного материала Итог урока Домашнее задание

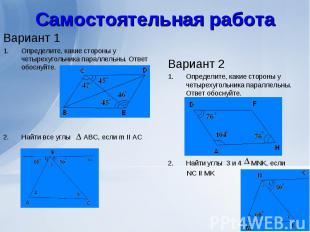
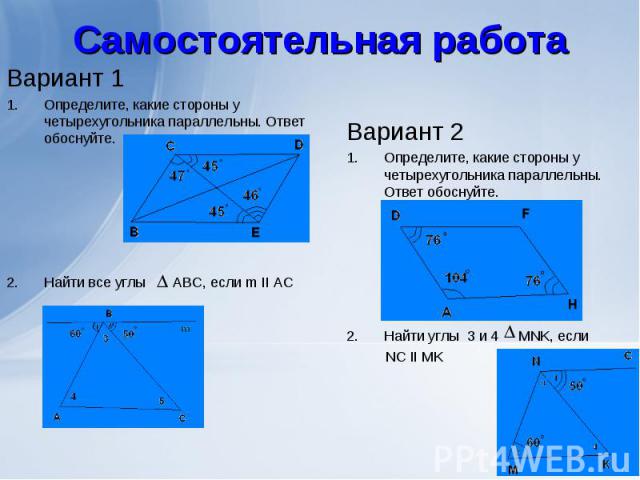
Вариант 1 Вариант 1 Определите, какие стороны у четырехугольника параллельны. Ответ обоснуйте. Найти все углы ABC, если m II AC

Проверим устно решение второй задачи. Проверим устно решение второй задачи. Сформулируйте определение, признаки параллельности прямых и свойств углов (внутренних накрестлежащих и внутренних односторонних углов) при параллельных прямых и секущей.

Евклид (3 век до нашей эры) Евклид (3 век до нашей эры) В труде «Начала» приводит такое определение: «Параллельные суть прямые, которые находятся в одной плоскости, и будучи продолжены в обе стороны неограниченно, ни стой, ни с другой стороны между собой не встречаются.»

Посидоний (1 век до нашей эры) Посидоний (1 век до нашей эры) «Две прямые лежащие в одной плоскости равностоящие друг от друга»

Папп Папп (вторая половина 3 век до нашей эры) древнегреческий ученый ввел символ параллельности прямых – знак

Риккардо (1720 - 1823) Риккардо (1720 - 1823) Впоследствии английский экономист Риккардо этот символ использовал как знак равенства.

Только в XVIII веке стали использовать символ параллельности прямых – знак Только в XVIII веке стали использовать символ параллельности прямых – знак

Ни на миг не прерывается живая связь между поколениями, ежедневно мы усваиваем опыт, накопленный предками. Древние греки на основе наблюдений и из практического опыта делали выводы, высказывали предположения – гипотезы, пытались обосновать и доказать. Ни на миг не прерывается живая связь между поколениями, ежедневно мы усваиваем опыт, накопленный предками. Древние греки на основе наблюдений и из практического опыта делали выводы, высказывали предположения – гипотезы, пытались обосновать и доказать.

В это время и сложилось утверждение: В это время и сложилось утверждение: «В споре рождается истина.»

Вариант 1 Вариант 1 Опытным путем определите, чему равна сумма углов треугольника (использовать транспортир, модели остроугольного, тупоугольного и прямоугольного треугольников).

Сумма углов треугольника равна 180º. Сумма углов треугольника равна 180º. Углы треугольника образуют развернутый угол.

Можно ли быть уверенным в том, что в каждом треугольнике сумма углов равна 180º? Можно ли быть уверенным в том, что в каждом треугольнике сумма углов равна 180º? Можно ли измерить углы любого треугольника?

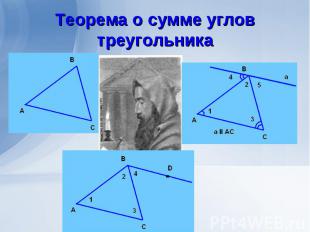
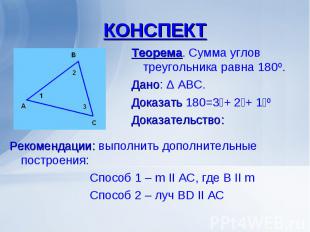
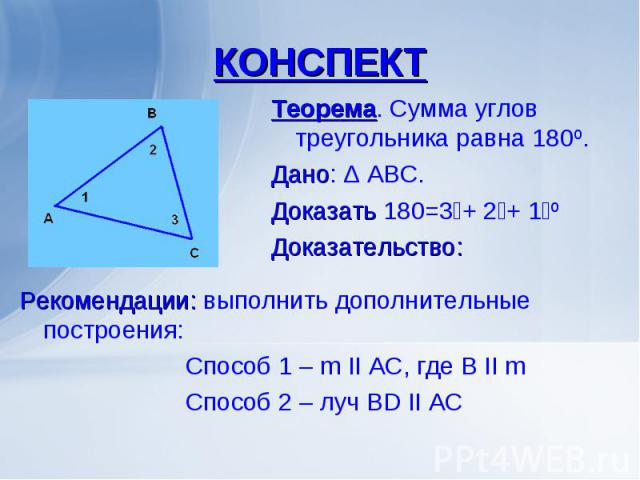
Теорема. Сумма углов треугольника равна 180º. Теорема. Сумма углов треугольника равна 180º. Дано: Δ АВС. Доказать ے1 +ے2 +ے3=180º Доказательство:

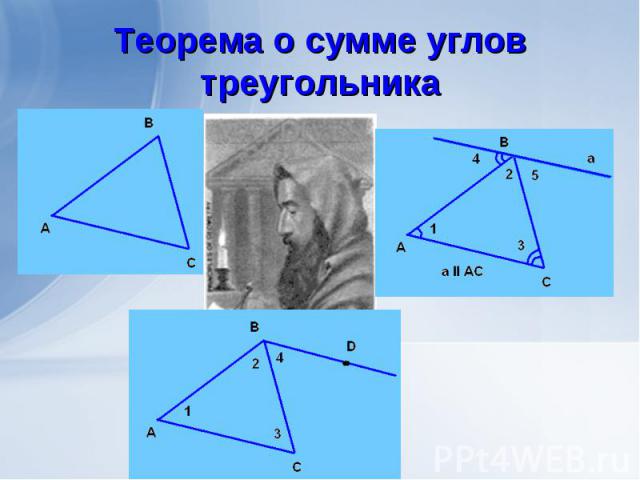
Первое доказательство было сделано еще Пифагором ( 5 век до нашей эры) В первой книге «Начал» Евклид излагает другое доказательство теоремы о сумме углов треугольника. Первое доказательство было сделано еще Пифагором ( 5 век до нашей эры) В первой книге «Начал» Евклид излагает другое доказательство теоремы о сумме углов треугольника. Попробуйте доказать дома эту теорему, используя чертеж учеников Пифагора.

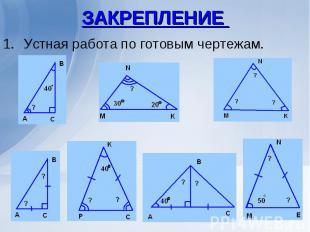
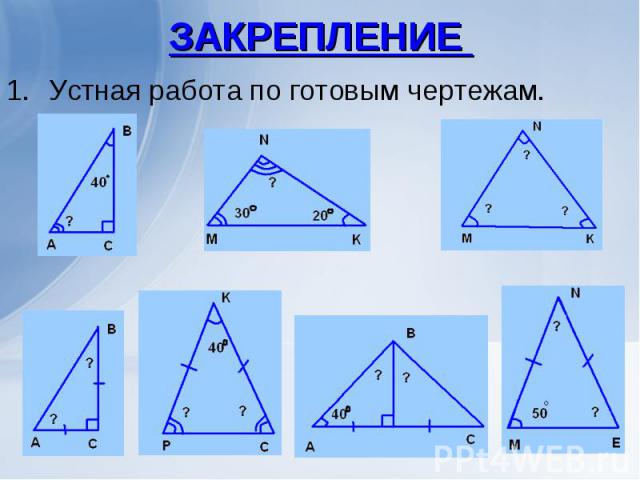
Устная работа по готовым чертежам. Устная работа по готовым чертежам.

Письменная работа Письменная работа по учебнику. Стр.53 №19 (2), №22 (1), №23 (2),

№19 (2) №19 (2) Пусть коэффициент пропорциональности равен k , то ے1=2k град , ے 2=3k град , ے 3=4 k град. Сумма углов треугольника равна 180º, то 2k + 3k + 4 k = 180, 9 k = 180, k = 20. Таким образом, ے1= 2 ∙ 20 º =40 º, ے 2=3 ∙ 20 º =60 º, ے 3= 4 ∙ 20 º =80 º . Ответ: 40 º, 60 º, 80 º .

ےА = ےС = 55º по свойству равнобедренного треугольника. ےА = ےС = 55º по свойству равнобедренного треугольника. ےВ = 180º - ےА – ےС = 180º - 55º - 55º = 70º. Ответ: 70º.

По свойству равнобедренного треугольника: По свойству равнобедренного треугольника: ے А= ے С. Таким образом, ے А = ےС = (180 – 120)/2 = 30º. Ответ: 30 º.

Научиться доказывать теорему 4.4 Научиться доказывать теорему 4.4 (стр. 46), Решить задание №19 (1) на стр. 53.