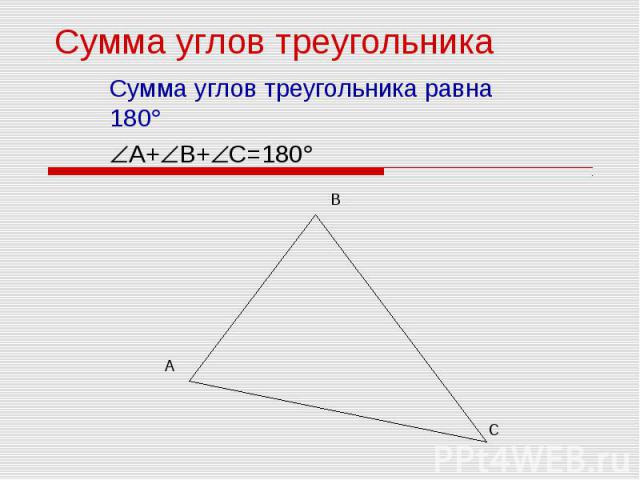
Презентация на тему: Сумма углов треугольника 3

Данные слайды используются при рассмотрении теоретического материала по теме: соотношения между сторонами и углами треугольника. Данные слайды используются при рассмотрении теоретического материала по теме: соотношения между сторонами и углами треугольника.

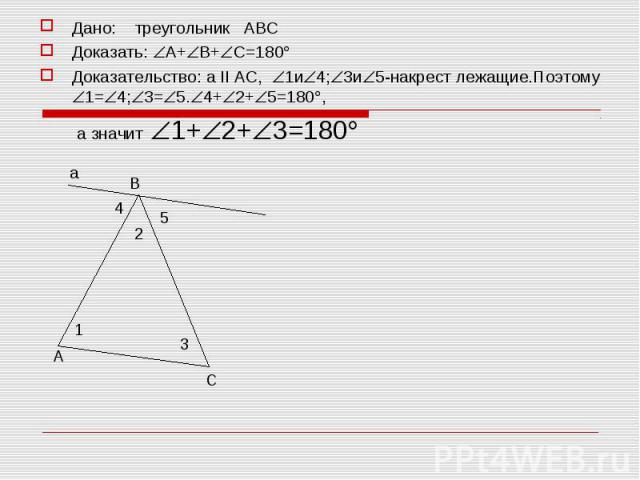
Дано: треугольник АВС Дано: треугольник АВС Доказать: А+ В+ С=180 Доказательство: а II АС, 1и 4; 3и 5-накрест лежащие.Поэтому 1= 4; 3= 5. 4+ 2+ 5=180 , а значит 1+ 2+ 3=180

Угол смежный с каким-нибудь углом треугольника называется внешним углом треугольника __ 4 Угол смежный с каким-нибудь углом треугольника называется внешним углом треугольника __ 4

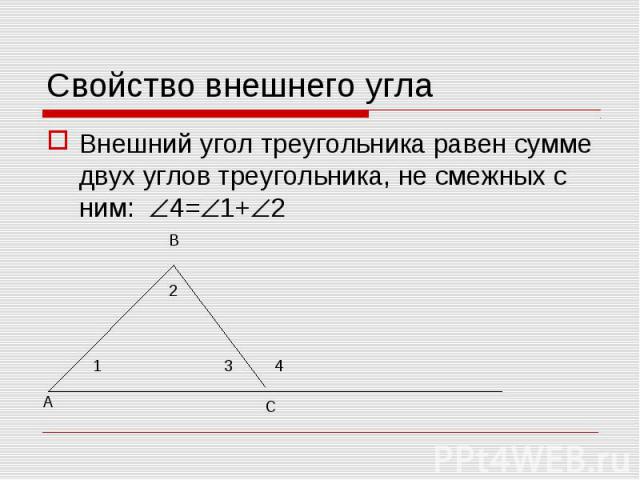
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: 4= 1+ 2 Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: 4= 1+ 2

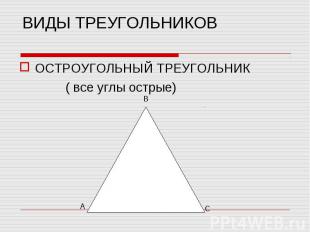
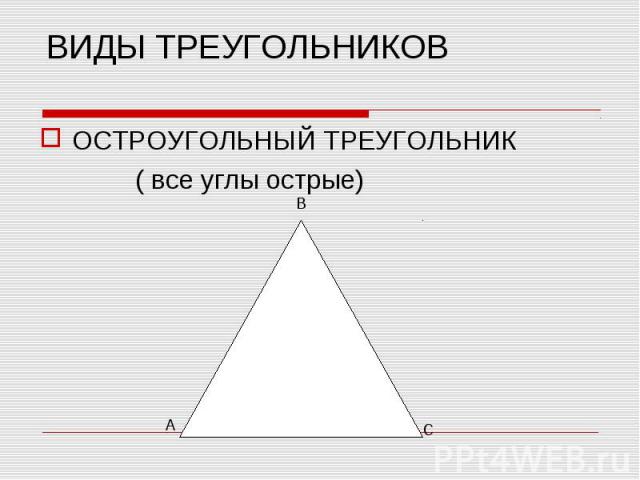
ОСТРОУГОЛЬНЫЙ ТРЕУГОЛЬНИК ОСТРОУГОЛЬНЫЙ ТРЕУГОЛЬНИК ( все углы острые)

Тупоугольный треугольник Тупоугольный треугольник (один из углов тупой, два других острые)

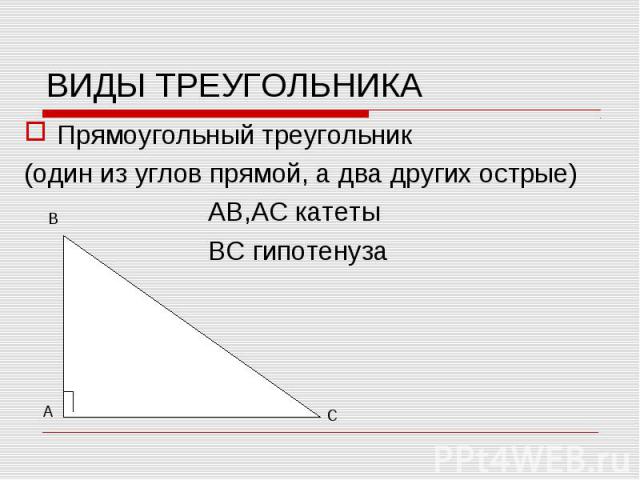
Прямоугольный треугольник Прямоугольный треугольник (один из углов прямой, а два других острые) АВ,АС катеты ВС гипотенуза

В треугольнике: 1) против большей стороны лежит больший угол; В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона. 1)АС большая сторона, значит В больший. 2) В большей, значит АС большая сторона.

1. В прямоугольном треугольнике гипотенуза больше катета. 1. В прямоугольном треугольнике гипотенуза больше катета. Если в треугольнике два угла равны, то треугольник равнобедренный( признак равнобедренного треугольника).

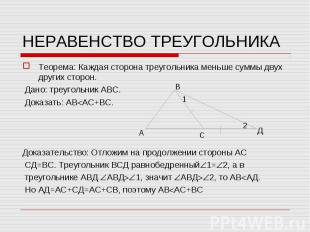
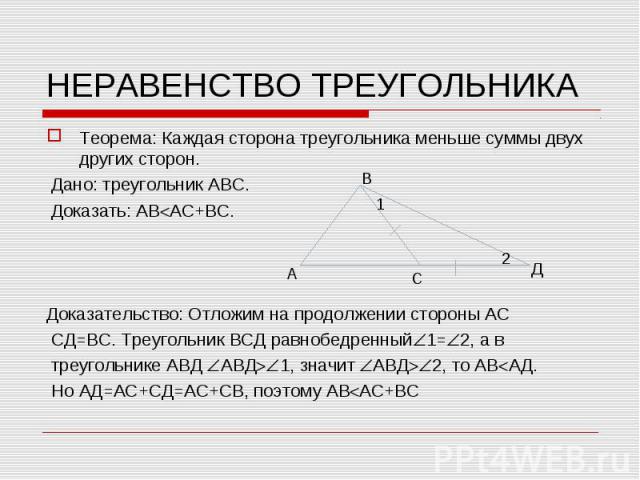
Теорема: Каждая сторона треугольника меньше суммы двух других сторон. Теорема: Каждая сторона треугольника меньше суммы двух других сторон. Дано: треугольник АВС. Доказать: АВ АС+ВС. Доказательство: Отложим на продолжении стороны АС СД=ВС. Треугольник ВСД равнобедренный 1= 2, а в треугольнике АВД АВД 1, значит АВД 2, то АВ АД. Но АД=АС+СД=АС+СВ, поэтому АВ АС+ВС

ДЛЯ ЛЮБЫХ ТРЁХ ТОЧЕК А,В И С, не лежащих на одной прямой, справедливы неравенства: ДЛЯ ЛЮБЫХ ТРЁХ ТОЧЕК А,В И С, не лежащих на одной прямой, справедливы неравенства: АВ АС+ВС; АС АВ+ВС; ВС ВА+АС.

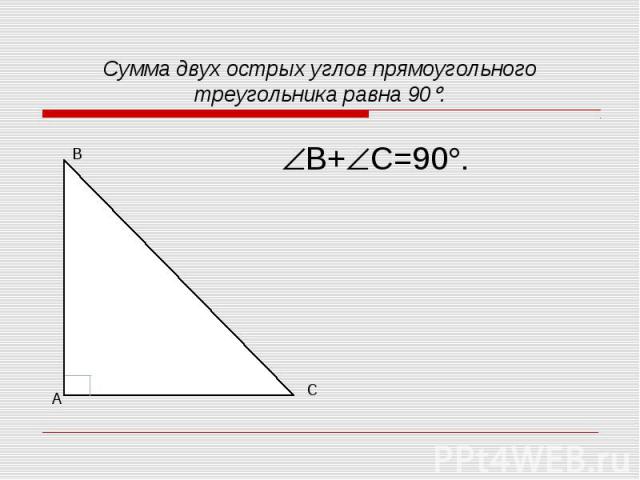
1. Сумма двух острых углов прямоугольного треугольника равна 90 . 1. Сумма двух острых углов прямоугольного треугольника равна 90 . 2. Катет прямоугольного треугольника, лежащий против угла в 30 , равен половине гипотенузы. 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 .

Рассмотрим треугольник АВС, где А=90 , В=30 и С=60 . Док-ть, что АС=½ВС. Рассмотрим треугольник АВС, где А=90 , В=30 и С=60 . Док-ть, что АС=½ВС.

Рассмотрим прямоугольный треугольник АВС, у которого катет АС равен половине гипотенузы ВС. Докажем, что АВС=30 Рассмотрим прямоугольный треугольник АВС, у которого катет АС равен половине гипотенузы ВС. Докажем, что АВС=30 Приложим к треугольнику АВС равный ему треугольник АВД, получим равно- сторонний треугольник ВСД, где Д= С= ДВС=60 . ДВС=2 АВС, следовательно, АВС=30 .

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

Если гипотенуза и острый угол одного прямоугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. Если гипотенуза и острый угол одного прямоугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

Если гипотенуза и катет одного прямоугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны. Если гипотенуза и катет одного прямоугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.