Презентация на тему: Основы математической логики. Логические операции

СЛОВО ЛОГИКА ОЗНАЧАЕТ СОВОКУПНОСТЬ ПРАВИЛ, КОТОРЫМ ПОДЧИНЯЕТСЯ ПРОЦЕСС МЫШЛЕНИЯ. САМ ТЕРМИН "ЛОГИКА" ПРОИСХОДИТ ОТ ДРЕВНЕГРЕЧЕСКОГО LOGOS, ОЗНАЧАЮЩЕГО "СЛОВО, МЫСЛЬ, ПОНЯТИЕ, РАССУЖДЕНИЕ, ЗАКОН".

ФОРМАЛЬНАЯ ЛОГИКА - НАУКА О ФОРМАХ И ЗАКОНАХ МЫШЛЕНИЯ. Основными формами мышления являются понятия, суждения и умозаключения.

ПОНЯТИЕ - ЭТО ФОРМА МЫШЛЕНИЯ, КОТОРАЯ ВЫДЕЛЯЕТ СУЩЕСТВЕННЫЕ ПРИЗНАКИ ПРЕДМЕТА ИЛИ КЛАССА ПРЕДМЕТОВ, ОТЛИЧАЮЩИЕ ЕГО ОТ ДРУГИХ. НАПРИМЕР, КОМПЬЮТЕР, ЧЕЛОВЕК, УЧЕНИКИ.

СУЖДЕНИЯ - ЭТО ФОРМА МЫШЛЕНИЯ, В КОТОРОЙ УТВЕРЖДАЕТСЯ ИЛИ ОТРИЦАЕТСЯ СВЯЗЬ МЕЖДУ ПРЕДМЕТОМ И ЕГО ПРИЗНАКОМ, ОТНОШЕНИЯ МЕЖДУ ПРЕДМЕТАМИ ИЛИ ФАКТ СУЩЕСТВОВАНИЯ ПРЕДМЕТА И КОТОРАЯ МОЖЕТ БЫТЬ ЛИБО ИСТИННОЙ, ЛИБО ЛОЖНОЙ.

"ДВАЖДЫ ДВА РАВНО ЧЕТЫРЕМ" - ИСТИННОЕ СУЖДЕНИЕ "ПРОЦЕССОР ПРЕДНАЗНАЧЕН ДЛЯ ПЕЧАТИ" - ЛОЖНОЕ.

Суждения могут быть простыми и сложными. "Весна наступила, и грачи прилетели" - сложное суждение, состоящее из двух простых. Простые суждения (высказывания) выражают связь двух понятий. Сложные - состоят из нескольких простых суждений.

СУЖДЕНИЯ В МАТЕМАТИЧЕСКОЙ ЛОГИКЕ НАЗЫВАЮТ ВЫСКАЗЫВАНИЯМИ ИЛИ ЛОГИЧЕСКИМИ ВЫРАЖЕНИЯМИ.

  УМОЗАКЛЮЧЕНИЕ - ПРИЕМ МЫШЛЕНИЯ, ПОЗВОЛЯЮЩИЙ НА ОСНОВЕ ОДНОГО ИЛИ НЕСКОЛЬКИХ СУЖДЕНИЙ-ПОСЫЛОК ПОЛУЧИТЬ НОВОЕ СУЖДЕНИЕ (ЗНАНИЕ ИЛИ ВЫВОД). ПРИМЕРАМИ УМОЗАКЛЮЧЕНИЙ ЯВЛЯЮТСЯ ДОКАЗАТЕЛЬСТВА ТЕОРЕМ В ГЕОМЕТРИИ.

МАТЕМАТИЧЕСКАЯ ЛОГИКА  ИЗУЧАЕТ ВОПРОСЫ ПРИМЕНЕНИЯ МАТЕМАТИЧЕСКИХ МЕТОДОВ ДЛЯ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ И ПОСТРОЕНИЯ ЛОГИЧЕСКИХ СХЕМ, КОТОРЫЕ ЛЕЖАТ В ОСНОВЕ РАБОТЫ ЛЮБОГО КОМПЬЮТЕРА.

Логическое выражение - это символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).

Простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно.

СУЩЕСТВУЮТ РАЗНЫЕ ВАРИАНТЫ ОБОЗНАЧЕНИЯ ИСТИННОСТИ И ЛОЖНОСТИ ПЕРЕМЕННЫХ: Истина И True 1 Ложь Л False 0

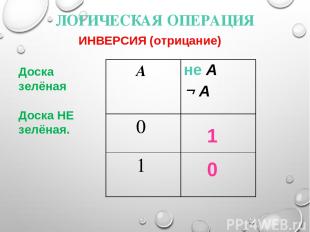
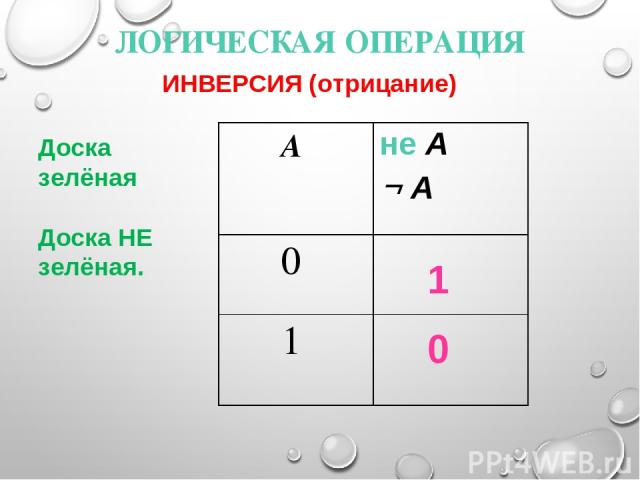
ЛОГИЧЕСКАЯ ОПЕРАЦИЯ 1 0 ИНВЕРСИЯ (отрицание) Доска зелёная Доска НЕ зелёная. A не A А 0 1

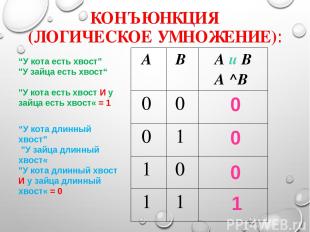
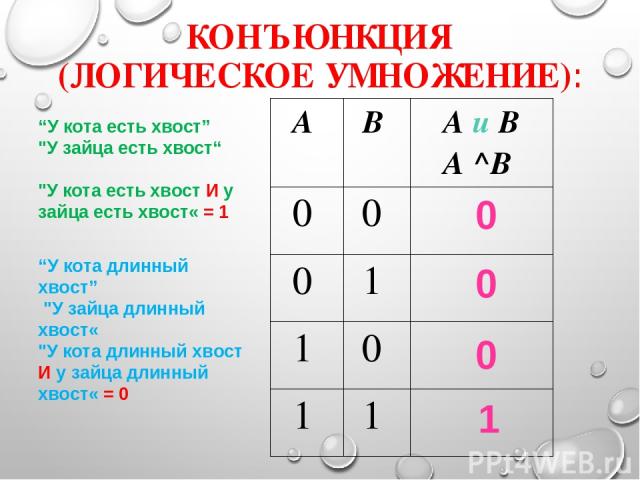
КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ): 0 0 0 1 “У кота есть хвост” "У зайца есть хвост“ "У кота есть хвост И у зайца есть хвост« = 1 “У кота длинный хвост”  "У зайца длинный хвост« "У кота длинный хвост И у зайца длинный хвост« = 0 А В A и B А ^В 0 0 0 1 1 0 1 1

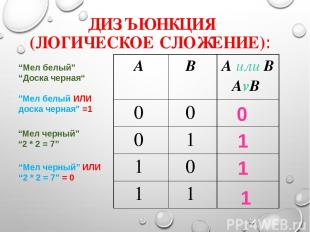
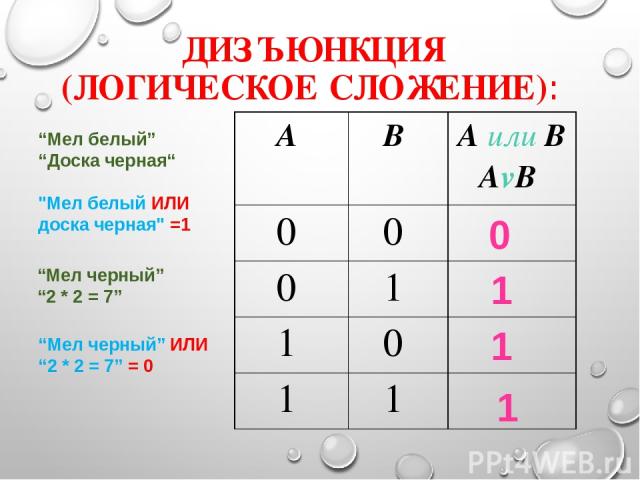
ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ): 1 1 1 0 “Мел белый” “Доска черная“ "Мел белый ИЛИ доска черная" =1 “Мел черный” “2 * 2 = 7” “Мел черный” ИЛИ “2 * 2 = 7” = 0 А В А или В AvB 0 0 0 1 1 0 1 1

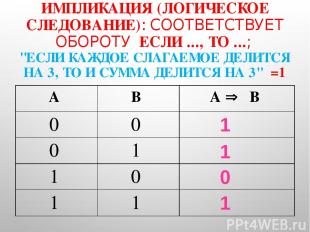
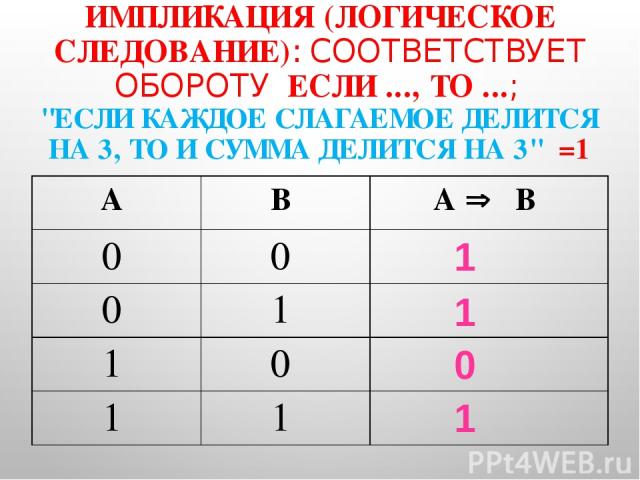
ИМПЛИКАЦИЯ (ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ): СООТВЕТСТВУЕТ ОБОРОТУ ЕСЛИ ..., ТО ...; "ЕСЛИ КАЖДОЕ СЛАГАЕМОЕ ДЕЛИТСЯ НА 3, ТО И СУММА ДЕЛИТСЯ НА 3" =1 1 1 0 1 А В А Þ   В 0 0 0 1 1 0 1 1

ЭКВИВАЛЕНЦИЯ (РАВНОЗНАЧНОСТЬ): СООТВЕТСТВУЕТ ОБОРОТАМ РЕЧИ ТОГДА И ТОЛЬКО ТОГДА; В ТОМ И ТОЛЬКО В ТОМ СЛУЧАЕ; 1 0 0 1 “ железо тяжелое” И “пух легкий” = 1 "железо легкое" И "пух тяжелый“ =1 А В А Û   В 0 0 0 1 1 0 1 1

ЛОГИЧЕСКИЕ ОПЕРАЦИИ ИМЕЮТ СЛЕДУЮЩИЙ ПРИОРИТЕТ: действия в скобках - инверсия & - конъюнкция V - дизъюнкция - импликация - эквиваленция

1) Число 376 четное и трехзначное. 2) Неверно, что Солнце движется вокруг Земли. Укажите истинность (ложность) высказываний.

ДЛЯ КАКОГО ИЗ УКАЗАННЫХ ЗНАЧЕНИЙ ЧИСЛА X ЛОЖНО ВЫРАЖЕНИЕ ( X > 2 ) ИЛИ НЕ ( X > 1)? 1) 1 2) 2 3) 3 4) 4

  а) (1v1)v(1v0);         б) ((1v0)v1) &1;         в) (0v1) Þ (1v0);         г) (0&1) Û  0;         д) 1&(1&1)&1;         е) ((1v0)&(1&1))&(0v1);         ж) ((1&0)v(1&0))v1;        з) ((1&1)v0) Þ (0v0);         и) ((0&0)v0) Û   (1v1). Укажите истинность (ложность) высказываний.

  а) (1v1)v(1v0); 1         б) ((1v0)v1) &1; 1         в) (0v1) Þ (1v0); 1         г) (0&1) Û  0; 1         д) 1&(1&1)&1; 1         е) ((1v0)&(1&1))&(0v1); 1         ж) ((1&0)v(1&0))v1; 1         з) ((1&1)v0) Þ (0v0); 0         и) ((0&0)v0) Û   (1v1). 0 Укажите истинность (ложность) высказываний.