Презентация на тему: Применение Формулы Пика

Применение Формулы Пика Выполнил: Парфенов Александр ученик 8 «Б» класса МБОУ «Лицей №124»Учитель: Скрылева Н.Н.

Георг Пик Формула Пика была открыта австрийским математиком Георгом Пиком в 1899г.

Краткая Биография. Георг Александр Пик (10 августа 1859 — 13 июля 1942) — австрийский математик, родился в еврейской семье. Мать — Йозефа Шляйзингер, отец — Адольф Йозеф Пик.Георга, который был одарённым ребёнком, обучал отец, возглавлявший частный институт. В 16 лет Георг закончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. Шестнадцатого апреля 1880 года под руководством Лео Кёнигсбергера Пик защитил докторскую диссертацию «О классе абелевых интегралов».В Немецком университете в Праге в 1888 году Пик получил место экстраординарного профессора математики, затем в 1892-м стал ординарным профессором. В 1900—1901 годах занимал пост декана философского факультета.С его именем связаны матрица Пика, интерполяция Пика — Неванлинны, лемма Шварца — Пика. 13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.

Формула Пика Формула выполняется, если вершины многоугольника находятся в точках целочисленной решётки.В-количество целочисленных точек внутри многоугольника.Г-количество целочисленных точек на границе многоугольника.

Доказательство Теоремы Пика. Центральное место в наших рассуждениях будет занимать следующий факт. Если два данных многоугольника с вершинами в точках целочисленной решетки составляют один многоугольник, то соответствующие им числа R1 и R2 связаны с числом R для многоугольника, составленного из двух данных, равенством R = R1+R2

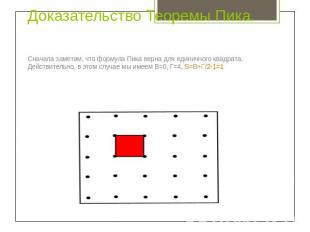
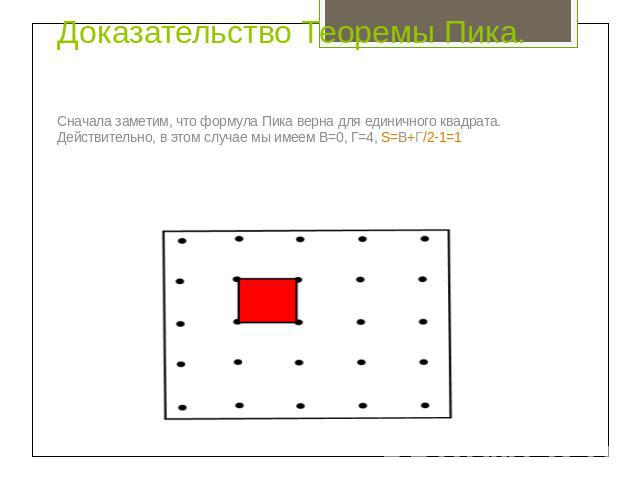
Доказательство Теоремы Пика. Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем В=0, Г=4, S=В+Г/2-1=1

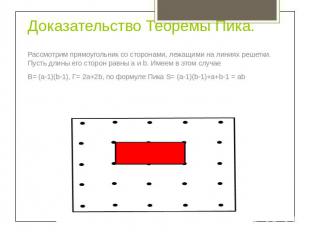
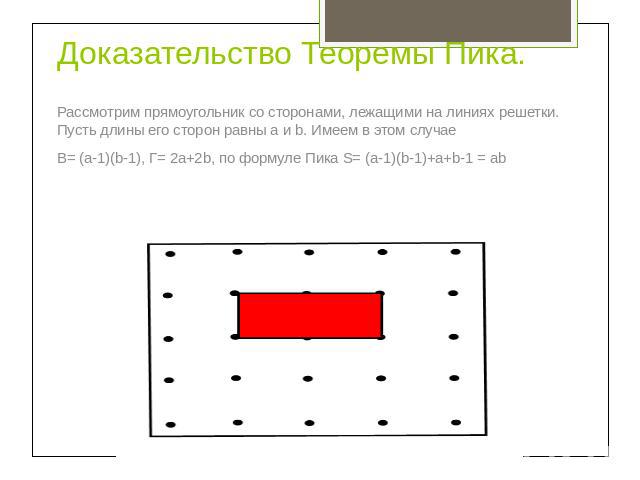
Доказательство Теоремы Пика. Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b. Имеем в этом случаеВ= (a-1)(b-1), Г= 2a+2b, по формуле Пика S= (a-1)(b-1)+a+b-1 = ab

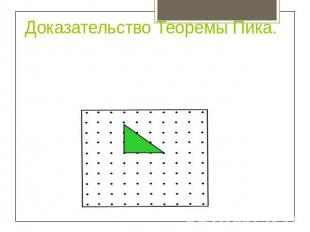
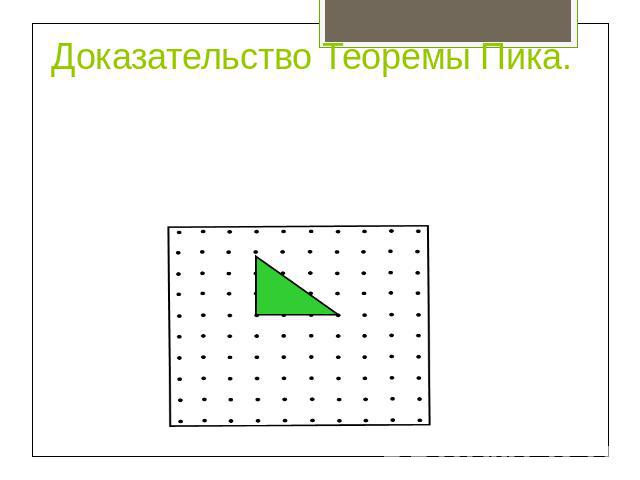
Доказательство Теоремы Пика. Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат   целочисленных точек. Тогда для этого случая █(а−1@В=(

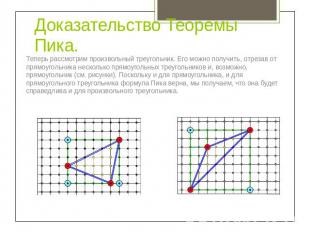
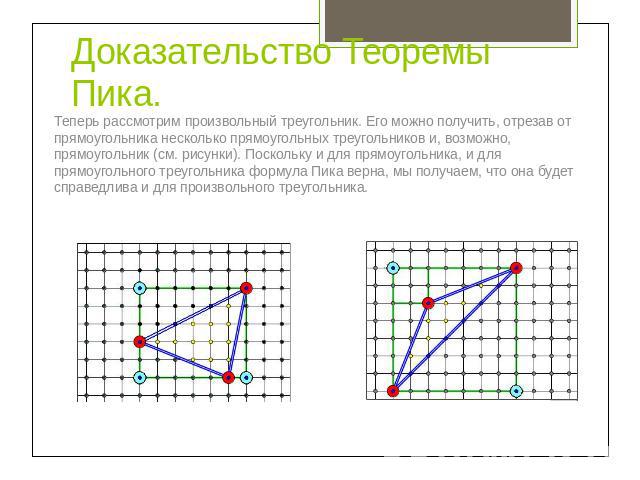
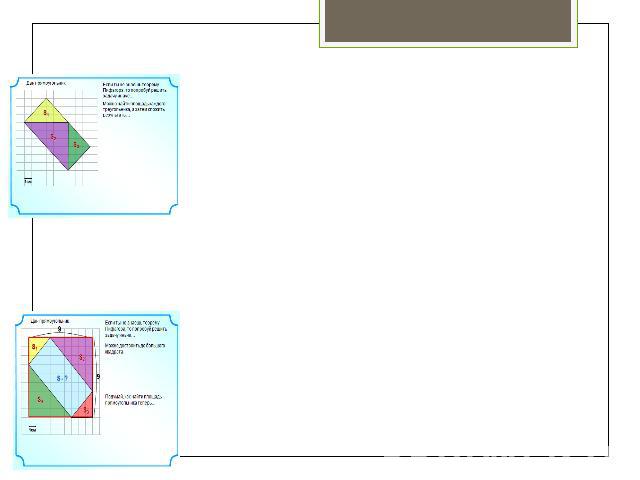
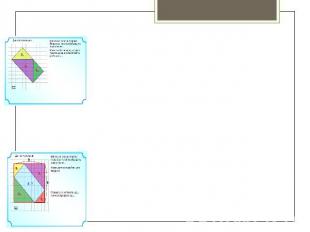
Доказательство Теоремы Пика. Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (см. рисунки). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

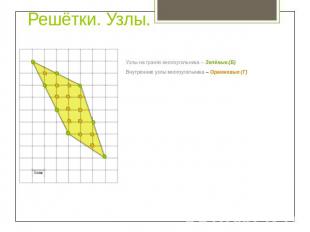
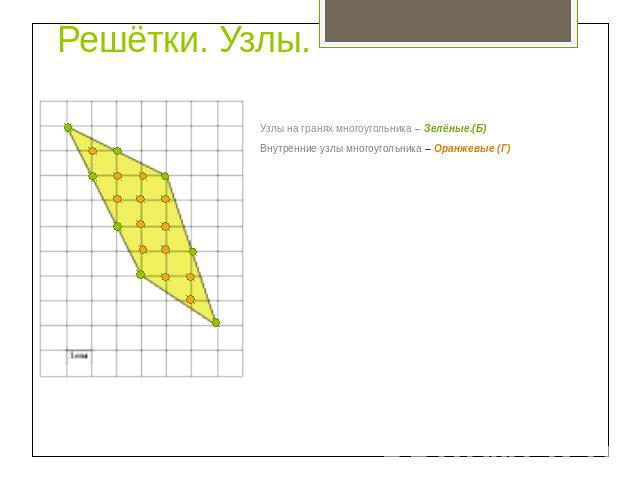
Решётки. Узлы. Узлы на гранях многоугольника – Зелёные.(Б)Внутренние узлы многоугольника – Оранжевые (Г)

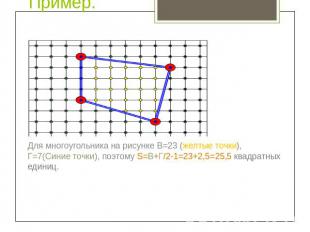
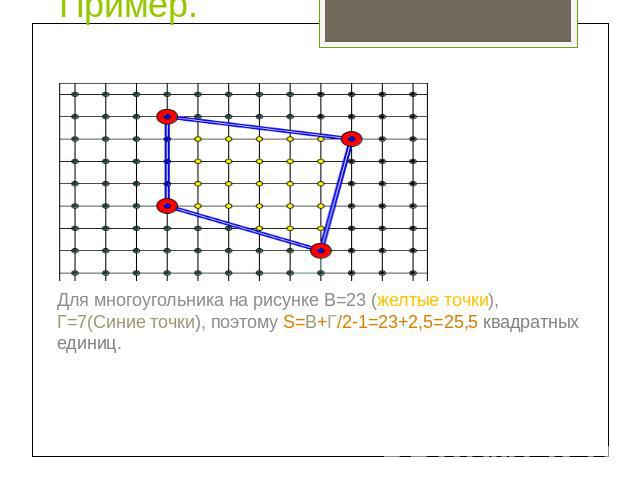
Пример. Для многоугольника на рисунке В=23 (желтые точки), Г=7(Синие точки), поэтому S=В+Г/2-1=23+2,5=25,5 квадратных единиц.

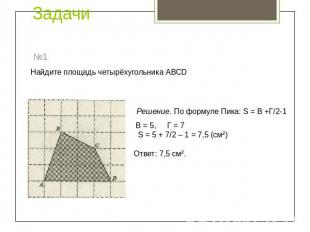
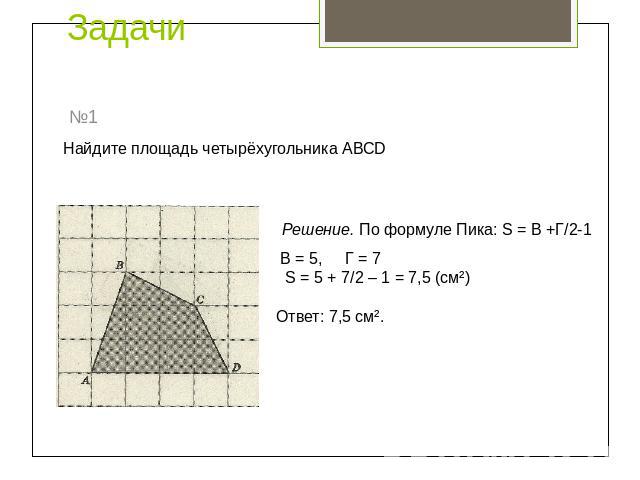
Задачи Найдите площадь четырёхугольника АВСDРешение. По формуле Пика: S = В +Г/2-1

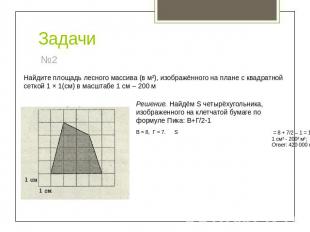
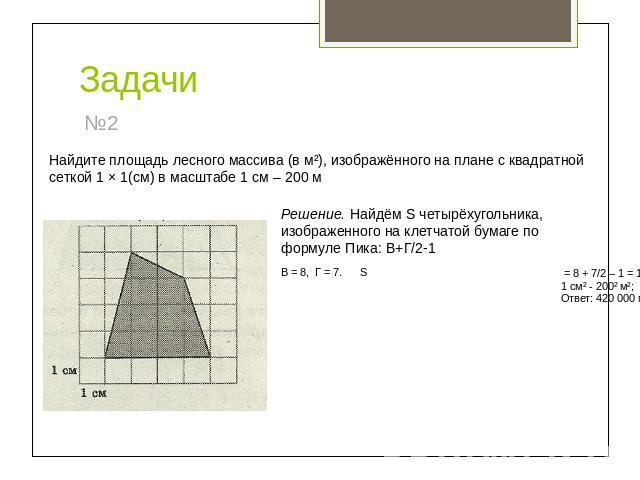
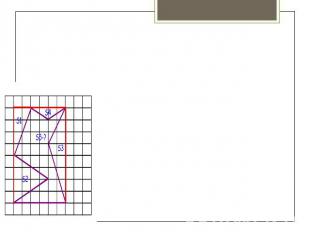
Задачи Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 мРешение. Найдём S четырёхугольника, изображенного на клетчатой бумаге по формуле Пика: В+Г/2-1