Презентация на тему: Теорема Виета

Урок алгебры в 8 классе

Цели урока: - повторить виды квадратных уравнений и формулы корней квадратного уравнения;- «открыть» зависимость между корнями и коэффициентами приведенного квадратного уравнения; сформулировать теорему Виета и показать ее применение для приведенных квадратных уравнений; - развивать интерес к математике, умения сравнивать и обобщать.

Повторение 1. Дайте определение квадратного уравнения Квадратным уравнением называют уравнение вида ах2+вх+с=0, где х- переменная, а, в и с – некоторые числа, а≠0 а – первый коэффициент в – второй коэффициент с – свободный член

2.Виды квадратных уравнений Полные квадратные уравнения Неполные квадратные уравнения Приведенные квадратные уравнения Неприведенные квадратные уравнения

3. Дайте определение приведенного квадратного уравнения. 4. Сколько корней может иметь квадратное уравнение? 5. Назовите формулы корней квадратных уравнений. Приведенным квадратным уравнением называется квадратное уравнение, первый коэффициент которого равен 1. х2 + bх + с = 0

Формулы корней квадратных уравнений ах²+bх+с=0 D=b²- 4ac – дискриминант D<0 D=0 D>0 Корней нет -b -b ± √D 2a Если b – четное число, т.е. b=2k, ТО -k ± √k² - ac

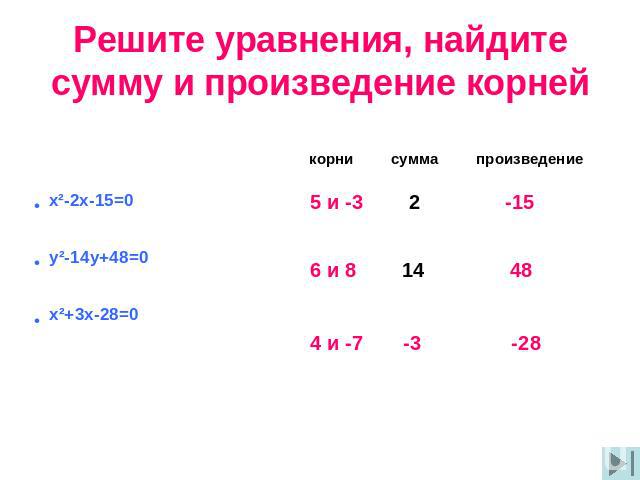
Решите уравнения, найдите сумму и произведение корней x²-2x-15=0 y²-14y+48=0 x²+3x-28=0

Изучение нового материала Сравните сумму и произведение корней с коэффициентами уравнений. Какая существует зависимость между корнями приведенного квадратного уравнения и его коэффициентами? Сформулируйте утверждение и найдите сумму и произведение корней следующего уравнения x²+bx +c=0 Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену x + x =-b x x = c

Франсуа Виет (1540-1603) Этот знаменитый французский ученый впервые установил зависимость между корнями и коэффициентами квадратного уравнения. Виет в 1591 году ввел буквенные обозначения для неизвестных и коэффициентов уравнений, что дало возможность записывать общими формулами корни и другие свойства уравнения. Недостатком алгебры Виета было то, что он признавал только положительные числа. Много разных открытий сделал Виет, но сам он больше всего дорожил установлением той зависимости, которая называется «теорема Виета».

Теорема Виета Теорема. Пусть х , x - корни квадратного уравнения ax²+bx+c=0. Тогда сумма корней равна –b/a, произведение корней равно с/а. Пусть х и х - корни приведенного квадратного уравнения х²+bx+c=0. Тогда сумма корней равна –b, а произведение корней равно с

Закрепление 1. Проверьте, правильно ли найдены корни квадратного уравнения: 1. x²+3x-40=0, x=-8 x=5 2. x²-2x-3=0, x=-1 x=3 2. У какого из данных уравнений сумма корней равна - 6, а произведение корней равно - 11 1. х²-6х+11=0 2. х²-11х-6=0 3. х²+6х-11=0

3. Составьте приведенное квадратное уравнение, если его корни равны: 1. x= -3, х=1; 2. x= - 3, x= - 4 3. x=5, x=6; 1.x²+2x-3=0 2. x²+7x+12=0 3. x²-11x+30=0 4. Можно ли назвать сумму корней квадратного уравнения x²-2x+3=0? Ответ: Это уравнение не имеет корней. 5. Определите знаки корней данного уравнения x²+4x-12=0 Ответ: Один корень положительный, а другой отрицательный, так как произведение корней равно -12.

Подведение итогов урока Сформулируйте теорему Виета для приведенного квадратного уравнения. Могут ли оба корня уравнения х²-2х-9=0 быть положительными? А сейчас посмотрим на дом, который мы построили.


Домашнее задание §24, № 960, № 967.