Презентация на тему: Обыкновенные дифференциальные уравнения

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.Задача Коши.

Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функций у = у(х). Их можно записать в виде где х — независимая переменная.

Наивысший порядок n входящей в уравнение (1) производной называется порядком дифференциального уравнения.

Решением дифференциального уравнения (1) называется всякая п раз дифференцируемая функция , которая после ее подстановки в уравнение превращает его в тождество.

Общее решение обыкновенного дифференциального уравнения n-го порядка (1) содержит n произвольных постоянных C1, С2, ... , Сn: Частное решение дифференциального уравнения получается из общего, если произвольным постоянным придать определенные значения.

задача Коши (дополнительные условия задаются в одной точке) краевая задача (дополнительные условия задаются в более чем одной точке)

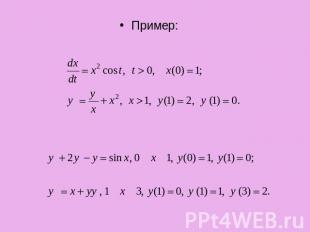
Пример:

Решение задачи Коши. сущность метода конечных разностей. состоит в следующем: 1. область непрерывного изменения аргумента (например, отрезок) заменяется дискретным множеством точек - узлами. Эти узлы составляют разностную сетку.

2. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке (сеточной функцией).3. Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции.

Такая замена дифференциального уравнения разностным называется его аппроксимацией на сетке (или разностной аппроксимацией). Таким образом, решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки.

Метод Эйлера. Рассмотрим уравнение с начальным условием для определенности будем считать, что решение нужно получить для значений х > x0.

1. выбирается достаточно малый шаг и строится система равноотстоящих точек2. Вычисляются

При этом искомая интегральная кривая проходящая через точку заменяется ломанной с вершинами .

Для оценки погрешности на практике пользуются двойным просчетом: с шагом h и шагом h/2.Погрешность более точного значения (при шаге h/2) оценивают приближенно так:где - значение точного решения уравнения при , -приближенное значение полученное при вычислениях с шагом h . - приближенное значение полученное с шагом h/2.

Рассмотрим систему двух уравнений первого порядкас начальными условиями

Приближенные значения вычисляются для этой системы по формулам

Модификации метода Эйлера. 1) Метод Эйлера-Коши

Оценка погрешности в точке , полученная с помощью двойного пересчета, имеет вид:где - значение точного решения уравнения при , -приближенное значение полученное при вычислениях с шагом h . - приближенное значение полученное с шагом h/2.

2) другая модификация метода Эйлера заключается в итерационном уточнении значения на каждом шаге.В качестве нулевого приближения берут

Далее строится итерационный процессИтерации продолжают до тех пор, пока для двух последовательных приближений не будет выполнено условие

Как правило, при достаточно малом h итерации быстро сходятся. Если после трех-четырех итераций не произошло совпадение нужного числа десятичных знаков, то следует уменьшить шаг расчета h.

Метод Рунге-Кутта.Рассмотрим уравнение с начальным условием

Если известно значение в точке , то вычисление приближенного значения в следующей точке производится по формулам:

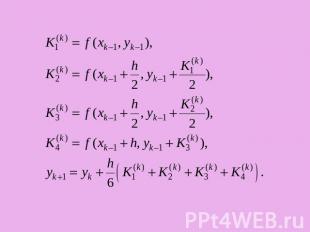
Оценку погрешности метода можно получить с помощью двойного просчета по формуле