Презентация на тему: Решение квадратных уравнений различными способами

МБОУ КОМСОМОЛЬСКАЯ СОШ УЧИТЕЛЬ МАТЕМАТИКИ ПЕРВОЙ КВ. КАТЕГОРИИ: БАЙЦЕВА Е.А. Решение квадратных уравнений различными способами

Герберт Спенсер, английский философ, когда-то сказал: “Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы”. Проверим, кто из вас порадовал бы Герберта Спенсера. План урока: ОМ Повторение теоретического материала (устная работа) Решение квадратных уравнений различными способами Самостоятельная работа Домашнее задание Итог урока Рефлексия

Цель урока: Обобщение навыков и систематизация знаний по теме «Квадратные уравнения», рассмотрение различных способов решения квадратного уравнения. Задачи урока: 1.Систематизировать знания, выработать умение выбирать рациональный способ решения квадратных уравнений; 2.Развивать логическое мышление, память, внимание; 3.Воспитывать культуру умственного труда.

Устно: Какие уравнения называются квадратными? Назовите виды квадратных уравнений. Какое уравнение называется неполным квадратным? Виды неполного квадратного уравнения и способы их решения. Какое уравнение называется приведённым квадратным? Какие способы его решения? От чего зависит количество корней полного квадратного уравнения? Как находится дискриминант? Сколько корней может иметь квадратное уравнение? Формулы корней квадратного уравнения

Выберите из данных вам уравнений то, которое проще решить данным способом: 2х2+14х=0; х2-25=0; 4х2-4х+1=0; х2-11х+18=0; 2х2-6х+4=0; 3х2+11х+5=0 (1 балл каждое задание) которое решается переносом слагаемых; которое решается вынесением общего множителя; по сумме коэффициентов; по теореме Виета; по общей формуле корней квадратного уравнения

Решите квадратные уравнения разными способами: 4х2-16х=0 (1балл) 2х2+3х-2=0 (2 балла) х2+2х-15=0 (2 балла) 4х2-4х+1=0 (2 балла) Защита у доски: 1 группа решают одно уравнение с помощью выделения полного квадрата, другое - графическим способом 2 группа решают одно уравнение способом разложения на множители, другое с помощью общей формулы корней квадратного уравнения 3 группа решают одно уравнение с помощью теоремы Виета, другое с помощью общей формулы корней квадратного уравнения, где b=2k.
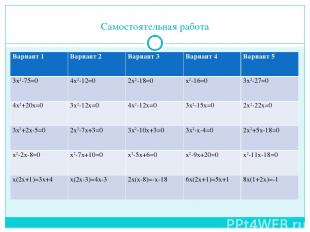
Самостоятельная работа Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 3х2-75=0 4х2-12=0 2х2-18=0 х2-16=0 3х2-27=0 4х2+20х=0 3х2-12х=0 4х2-12х=0 3х2-15х=0 2х2-22х=0 3х2+2х-5=0 2х2-7х+3=0 3х2-10х+3=0 3х2-х-4=0 2х2+5х-18=0 х2-2х-8=0 х2-7х+10=0 х2-5х+6=0 х2-9х+20=0 х2-11х-18=0 х(2х+1)=3х+4 х(2х-3)=4х-3 2х(х-8)=-х-18 6х(2х+1)=5х+1 8х(1+2х)=-1

Домашнее задание На оценку «3»: №28.5(в) – разными способами На оценку «4»:28.19(б) – разными способами На оценку «5»:29.26(а) – разными способами
Оценочный лист: в нё м проставляются баллы за проделанную работу В графе итог урока ставите + за каждый способ, если ты его усвоил Фамилия Выбор уравнений Разные способы уравнений Самостоятельная работа Дополнительное задание Итог урока