Презентация на тему: Преобразование графиков
Преобразование графиков функций Учитель математики Шахова Т. А. Гимназия №3 Г. Мурманск

Содержание Параллельный перенос вдоль оси OY Параллельный перенос вдоль оси ОХ Растяжение (сжатие) в k раз вдоль оси OY Растяжение (сжатие) в k раз вдоль оси OХ Симметричное отображение относительно оси OY Симметричное отображение относительно оси OX Построение графика y=|f(x)| Построение графика y=f(|x|)

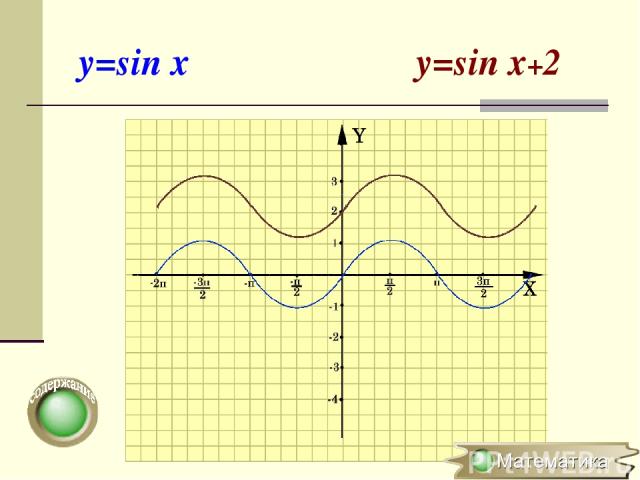
Параллельный перенос вдоль оси OY y=f(x) → y=f(x)+a (x0;y0) → (x0;y0+a) Для построения графика функции y=f(x)+a необходимо график функции y=f(x) перенести вдоль оси OY на вектор (0;а)
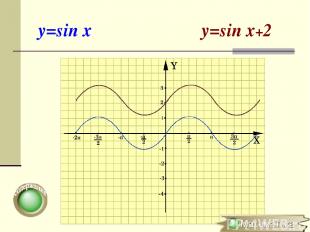
y=sin x y=sin x+2

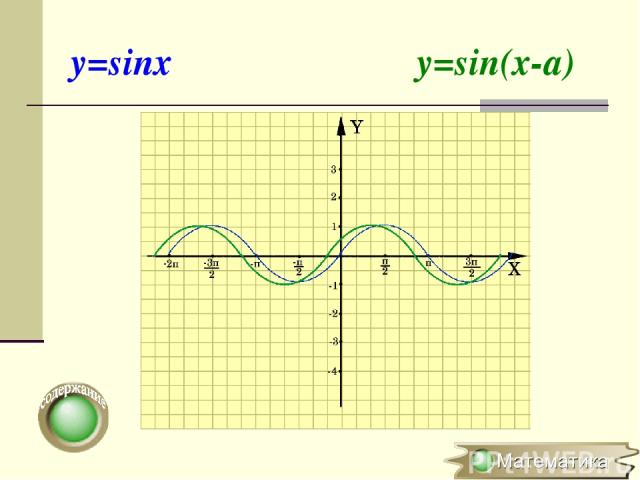
Параллельный перенос вдоль оси ОХ y=f(x) → y=f(x-a) (x0;y0) → (x0+a;y0) Для построения графика функции y=f(x-a) необходимо график функции y=f(x) перенести вдоль оси OX на вектор (0;а)
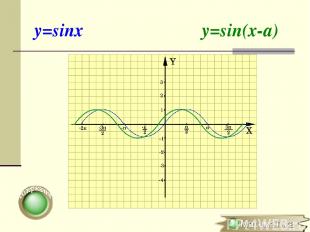
y=sinx y=sin(x-a)

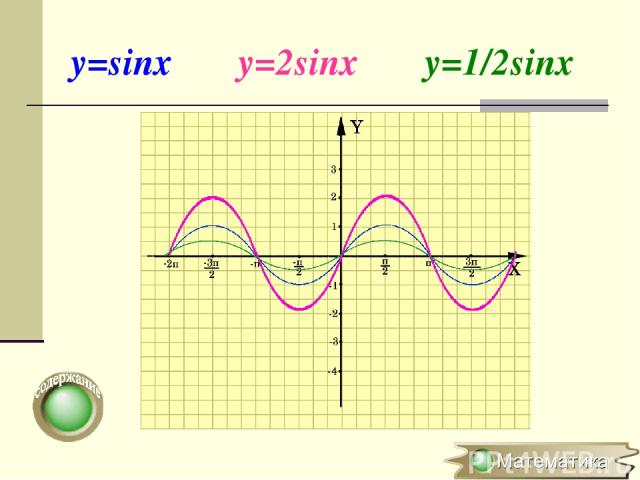
Растяжение (сжатие) в k раз вдоль оси OY y=f(x) → y=kf(x), где k>0 (x0;y0) → (x0;ky0) Для построения графика функции y=kf(x) необходимо график функции y=f(x) растянуть в k раз вдоль оси ОY для k >1 или сжать в 1/k развдоль оси OY для k
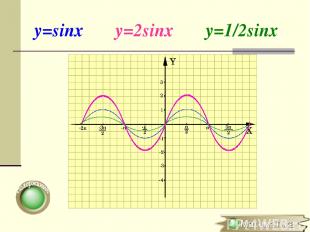
y=sinx y=2sinx y=1/2sinx

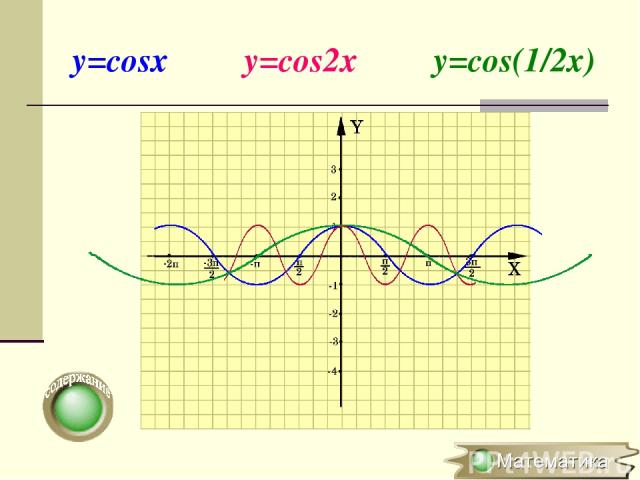
Растяжение (сжатие) в k раз вдоль оси OХ y=f(x) → y=f(kx), где k>0 (x0;y0) → ( x0;y0) Для построения графика функции y=f(kx) необходимо график функции y=f(x) сжать в k раз вдоль оси ОХ для k >1 или растянуть в 1/k раз вдоль оси OХ для k
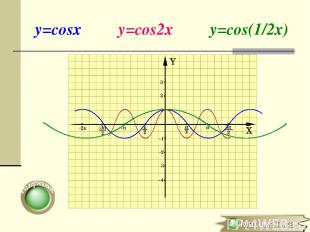
y=cosx y=cos2x y=cos(1/2x)

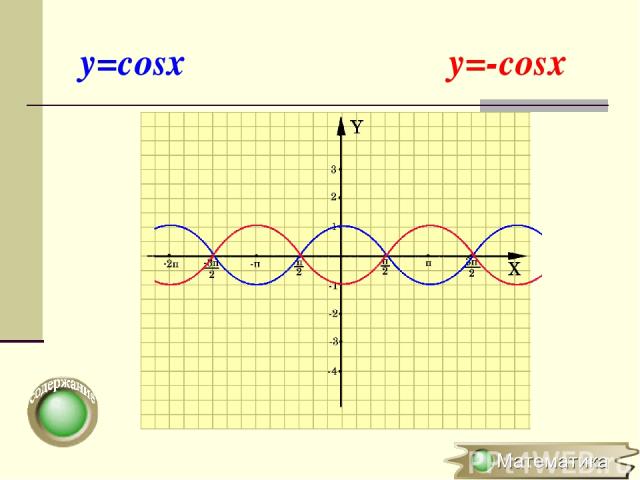
Симметричное отображение относительно оси OY y=f(x) → y=-f(x) (x0;y0) → (x0;-y0) Для построения графика функции y=-f(x) необходимо график функции y=f(x)симметрично отобразить относительно оси ОХ
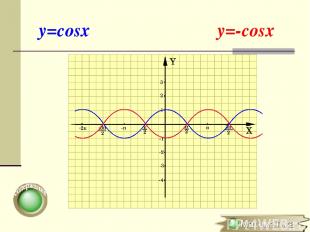
y=cosx y=-cosx

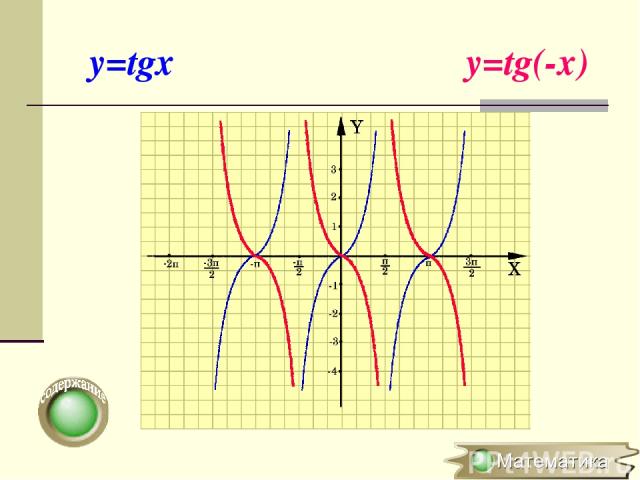
Симметричное отображение относительно оси OХ y=f(x) → y=f(-x) (x0;y0) → (-x0;y0) Для построения графика функции y=f(-x) необходимо график функции y=f(x) симметрично отобразить относительно оси ОY
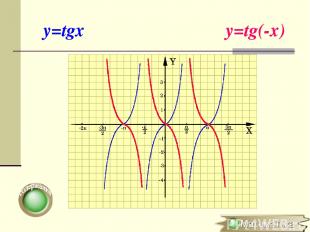
y=tgx y=tg(-x)

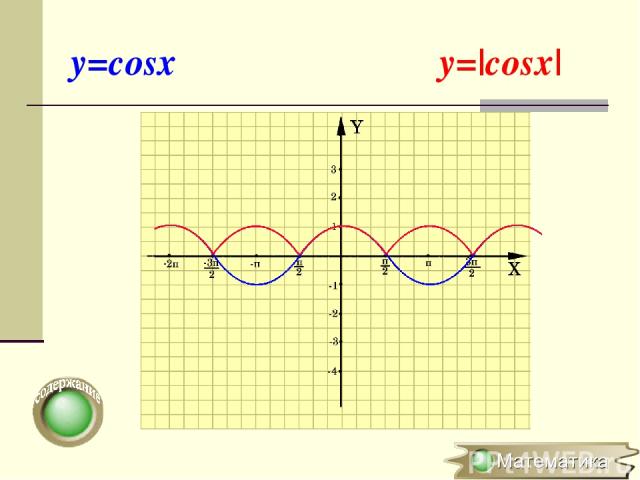
Построение графика y=|f(x)| Для построения графика функции y=|f(x)| необходимо часть графика функции y=f(x), лежащую выше оси OX, оставить неизменной, а часть графика y=f(x), лежащую ниже оси OХ, симметрично отобразить относительно оси ОХ f(x), если х 0 y=|f(x)|= -f(x), если х < 0
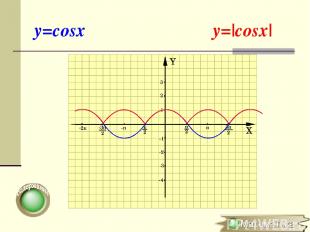
y=cosx y=|cosx|

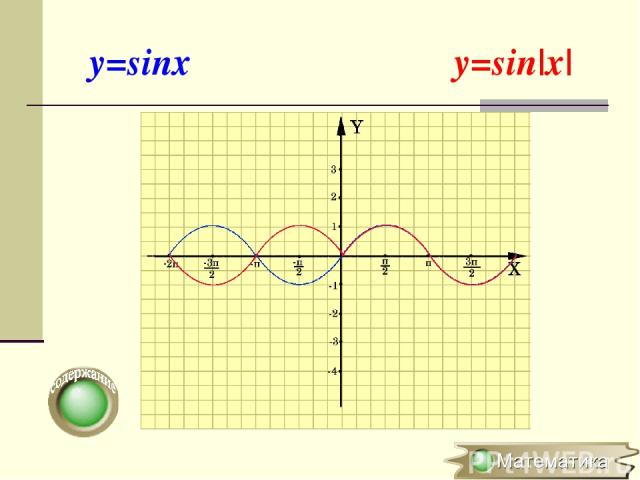
Построение графика y=f(|x|) f(x), если х 0 y=f(|x|)= f(-x), если х
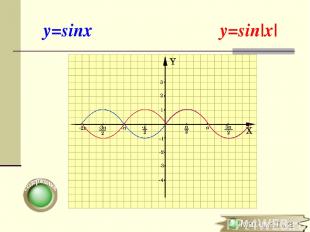
y=sinx y=sin|x|
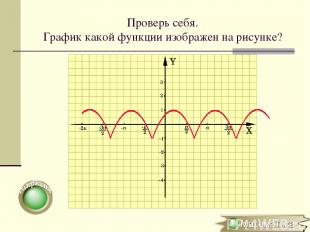
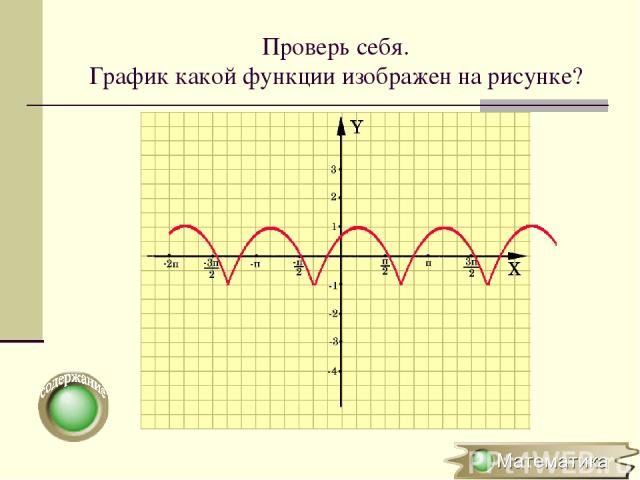
Проверь себя. График какой функции изображен на рисунке?