Презентация на тему: Понятие площади многоугольника

МАТЕМАТИЧЕСКИЙ ДИКТАНТ Четырехугольник, у которого противоположные стороны параллельны. Четырехугольник, у которого только две противоположные стороны параллельны. Параллелограмм, у которого все углы прямые. Точка, из которой выходят стороны четырехугольников. Сумма длин всех сторон. Отрезок, соединяющий противоположные вершины четырехугольника. Прямоугольник, у которого все стороны равны. Параллелограмм, у которого все стороны равны. Отрезок, соединяющий соседние вершины.

Людям часто приходилось делить землю по берегам Нила на участки. Подсчитывать площадь трудно, берега извилисты, границы участка неровные. И люди постепенно научились измерять такие площади, разбивая их на прямоугольные и треугольные участки (17 век до н. э.) Происхождение науки геометрии. Для чего нужно было измерять площади?

ПЛОЩАДЬ – это… некая величина, характеризующая геометрическую фигуру, расположенную на плоскости или на иной поверхности. Обычно площадь обозначается буквой S.

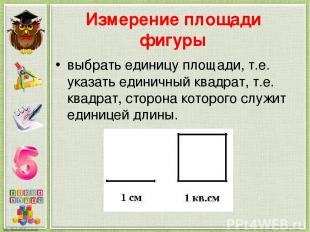
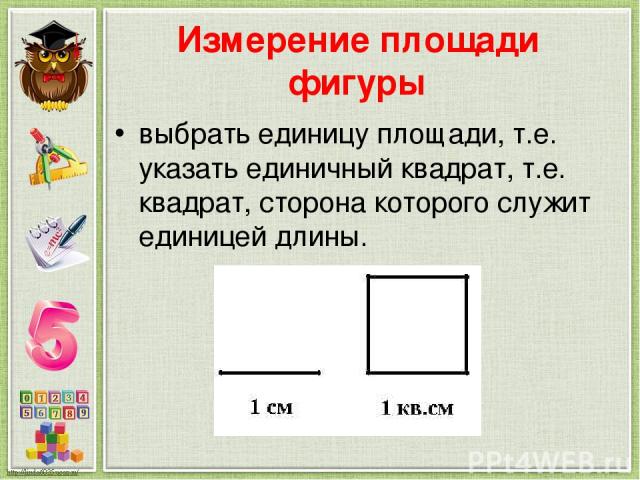
Измерение площади фигуры выбрать единицу площади, т.е. указать единичный квадрат, т.е. квадрат, сторона которого служит единицей длины.

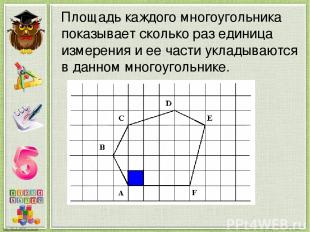
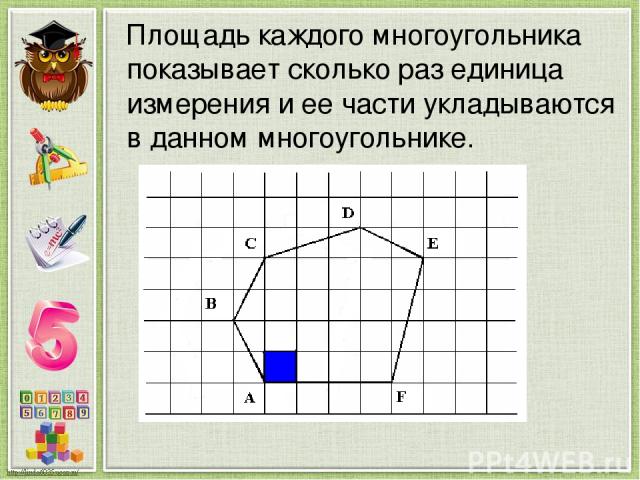
Площадь каждого многоугольника показывает сколько раз единица измерения и ее части укладываются в данном многоугольнике.

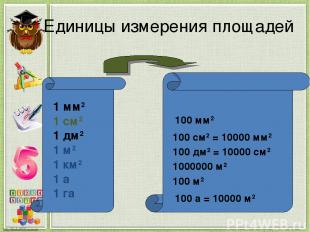
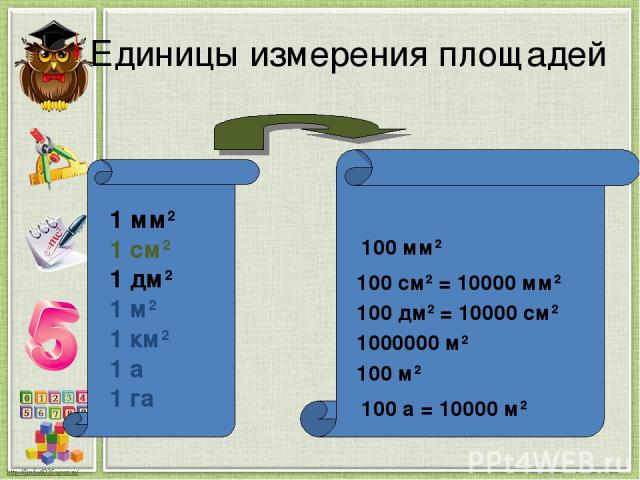
Единицы измерения площадей 1 мм2 1 см2 1 дм2 1 м2 1 км2 1 а 1 га 100 мм2 100 см2 = 10000 мм2 100 дм2 = 10000 см2 1000000 м2 100 м2 100 а = 10000 м2

Старинные меры площадей на Руси В 11 – 13 веках употреблялась мера «плуг» - это мера земли , с которой платили дань. Есть основание считать , что «плуг» - 8 – 9 гектаров. В 16 – 18 веках мерою полей служит «десятина»( равная 1,1 га) и «четверть»( равная половине десятины- поле, на котором высевали четверть хлеба). Десятина, которая в быту местами имела и другие размеры, делилась на 2 «четверти», четверть, в свою очередь, на 2 «осьмины», осьмина – на 2 «полуосьмины» ит.д. Налоговой единицей земли была «соха», в Новгороде «обжа», которая имела различные размеры, в зависимости от качества земли социального положения владельца. Позже землю измеряли «акрами» (4047 м2)

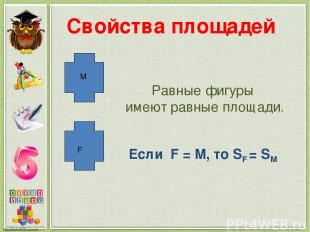
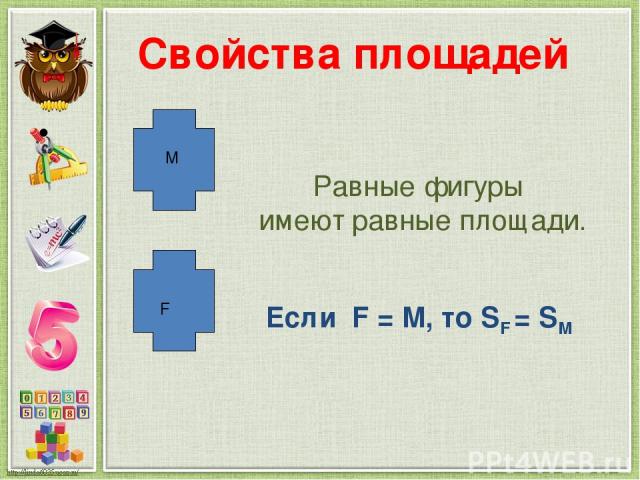
Свойства площадей Равные фигуры имеют равные площади. F М Если F = М, то SF = SM

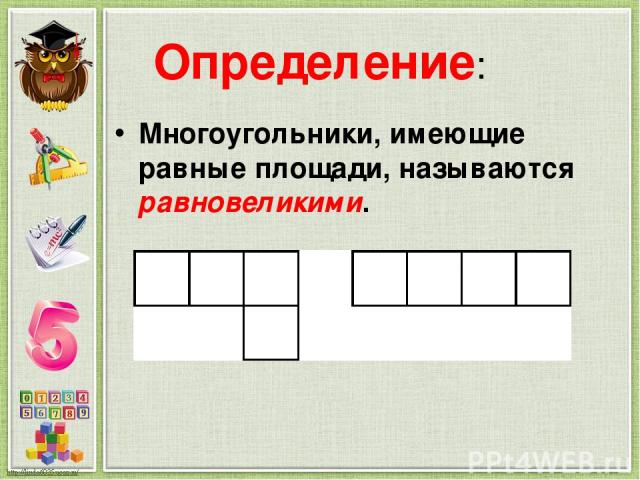
Определение: Многоугольники, имеющие равные площади, называются равновеликими.

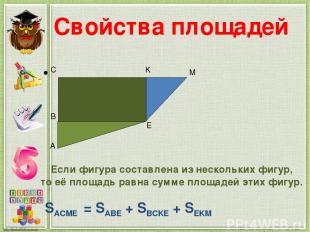
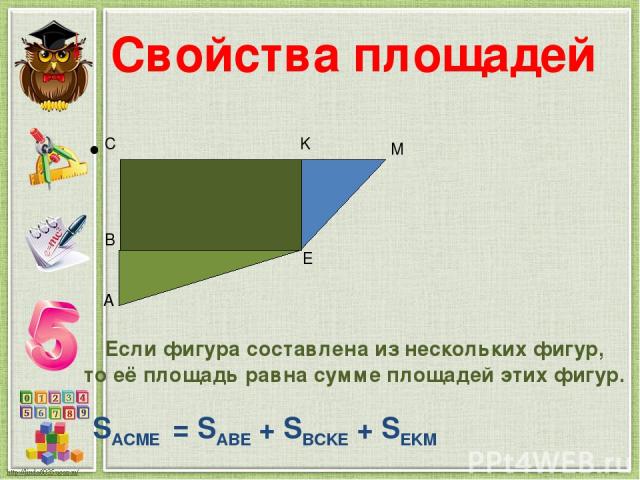
Свойства площадей Если фигура составлена из нескольких фигур, то её площадь равна сумме площадей этих фигур. SACME = SABE + SBCKE + SEKM

Свойства площадей Площадь квадрата равна квадрату его стороны. SABCD = a2

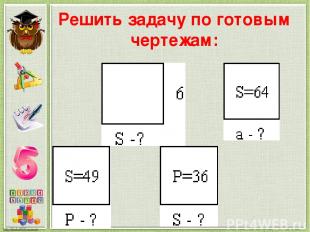
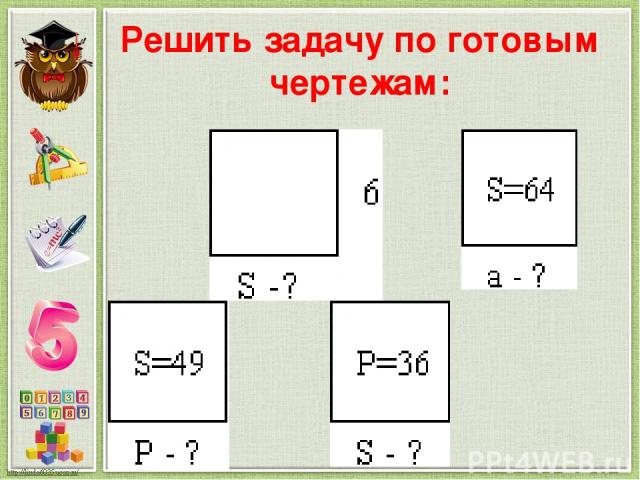
Решить задачу по готовым чертежам:

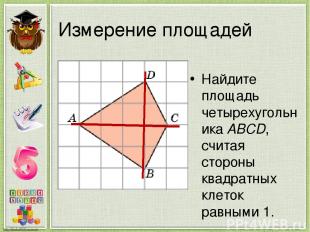
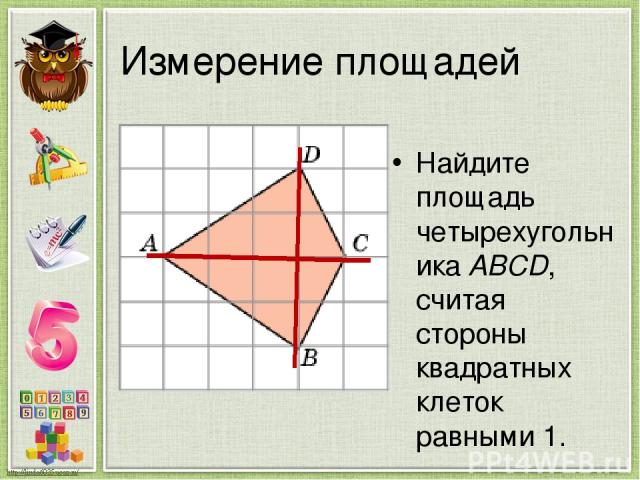
Измерение площадей Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.

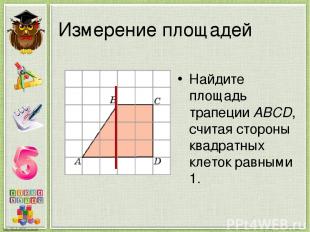
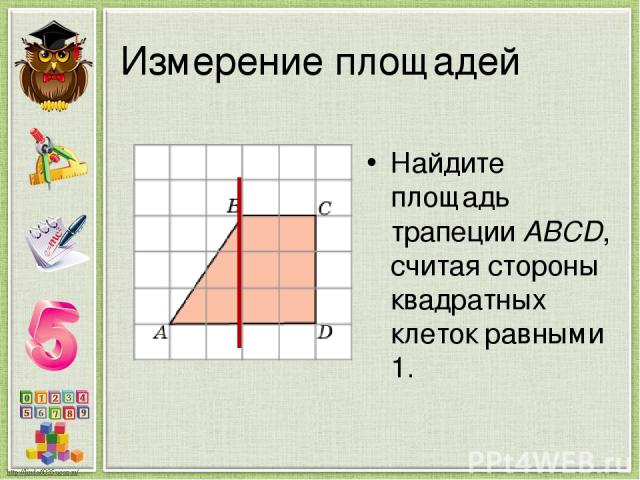
Измерение площадей Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.

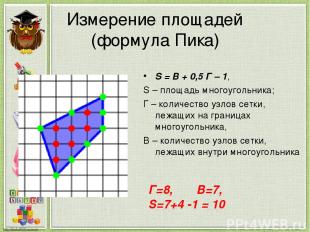
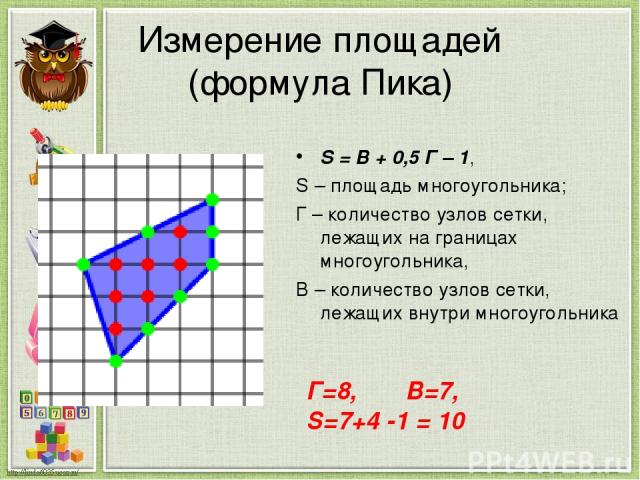
Измерение площадей (формула Пика) S = B + 0,5 Г – 1, S – площадь многоугольника; Г – количество узлов сетки, лежащих на границах многоугольника, В – количество узлов сетки, лежащих внутри многоугольника Г=8, В=7, S=7+4 -1 = 10

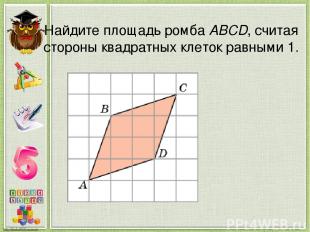
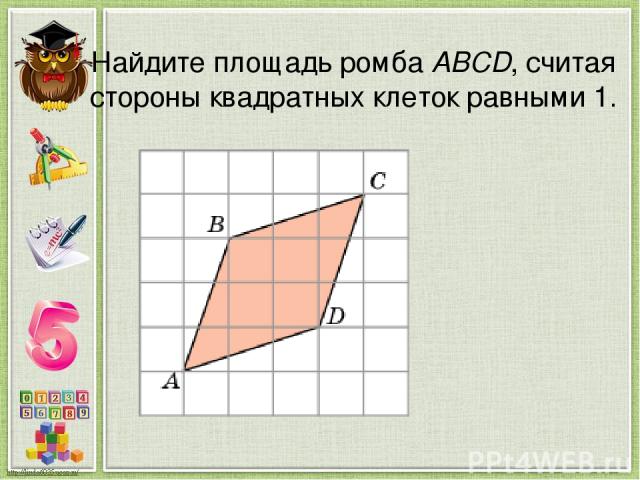
Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1.

Начертить квадрат, принять его за единицу измерения площадей. Начертить: а) квадрат, площадь которого выражена числом 4; б) прямоугольник, площадь которого выражена числом 4; в) треугольник, площадь которого выражена числом 2.

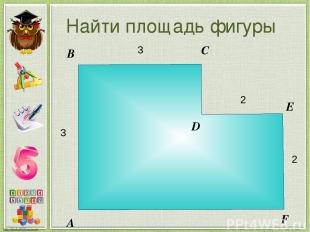
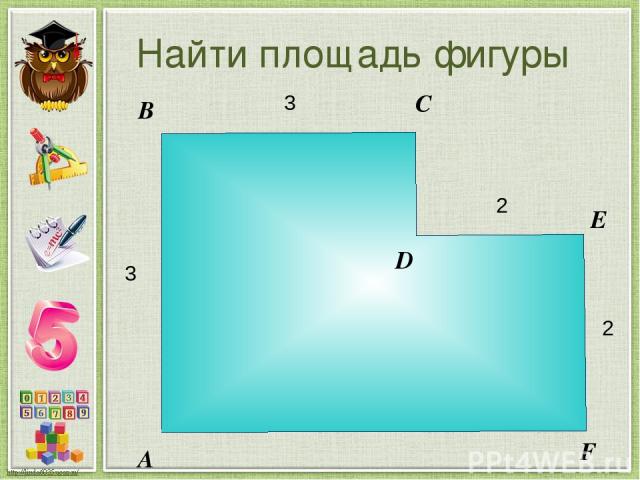
Найти площадь фигуры

Закончить предложение: квадрат это . . . Найти периметр квадрата со стороной 6 см. Найти площадь квадрата со стороной 4 м. Сравнить площади заштрихованных и незаштрихованных частей квадрата, изображенных на рисунке (учесть, что точки M, N – середины сторон)       Диагональ квадрата делит его на две фигуры. Эти фигуры являются: равными треугольниками равными квадратами равновеликими треугольниками произвольными треугольниками Самостоятельная работа

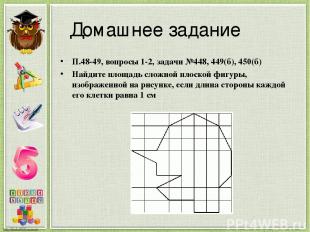
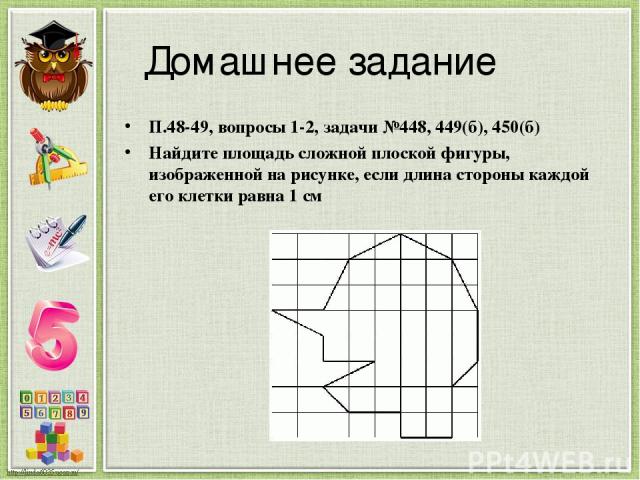
Домашнее задание П.48-49, вопросы 1-2, задачи №448, 449(б), 450(б) Найдите площадь сложной плоской фигуры, изображенной на рисунке, если длина стороны каждой его клетки равна 1 см

« Математику уже затем учить следует, что она ум в порядок приводит» М. В. Ломоносов