Презентация на тему: Основные понятия. Квадратные уравнения

Основные понятия. Квадратные уравнения. 8 класс Подготовила: учитель математики ГБОУ СОШ №3 «ОЦ» с. Кинель-Черкассы Елфимова Евгения Николаевна

Учиться вместе, а не просто что-то выполнять вместе. Вот суть данного подхода.

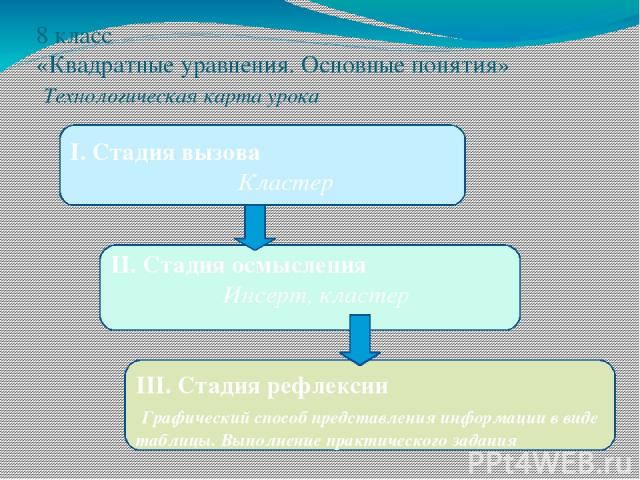
8 класс «Квадратные уравнения. Основные понятия» Технологическая карта урока I. Стадия вызова Кластер II. Стадия осмысления Инсерт, кластер III. Стадия рефлексии Графический способ представления информации в виде таблицы. Выполнение практического задания

Стадия вызова Работа с текстом Задание: 1. Из данных уравнений выберите квадратные 1) x2 – 1 =0; 2) x3+6x- 1=0; 3 ) - 4=0; 4) 5x=0; 5) 2x2 – 5x +6=0; 6) 7x – x2 + 3=0. 2.Прочитайте п.24 стр.133 учебника, найдите определения полного и неполного квадратного уравнения приведенного и неприведенного квадратного уравнения корня квадратного уравнения 3. Изобразите информацию в виде графического приема «гроздья»

Проверка 1.Квадратные уравнения: 2.Вопросы классу: сформулируйте определение квадратного уравнения по каким признакам вы отнесли данные уравнения к квадратным назовите значения коэффициентов выбранных уравнений 1) x2 – 1 =0 5) 2x2 – 5x +6=0 6) 7x – x2 + 3=0

Стадия осмысления Приемы Инсерт, кластер 1 этап – систематизация, оформление в кластер  2 этап – нахождение взаимосвязей между ветвями. 3 этап - мозговой штурм (идеи решения неполных квадратных уравнений) , прием Инсерт Квадратные уравнения ax2+bx+c=0

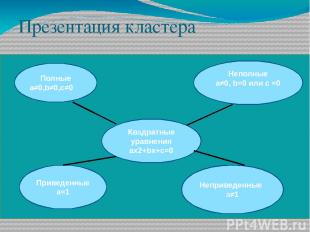
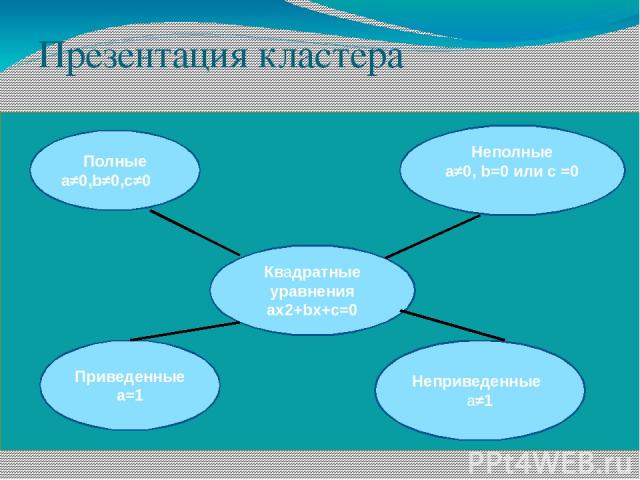
Презентация кластера Приведенные а=1 Полные а≠0,b≠0,c≠0 Квадратные уравнения ax2+bx+c=0 Неполные a≠0, b=0 или с =0 Неприведенные а≠1

Решение неполных квадратных уравнений ax2=0 ax2+bx=0 ax2+c=0 Чтение текста с пометками:    + я это знал    - я этого не знал    ! это меня удивило    ? хотел бы узнать подробнее

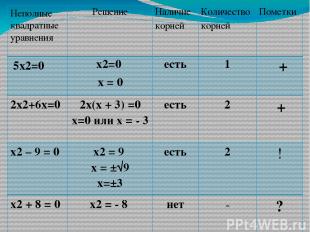
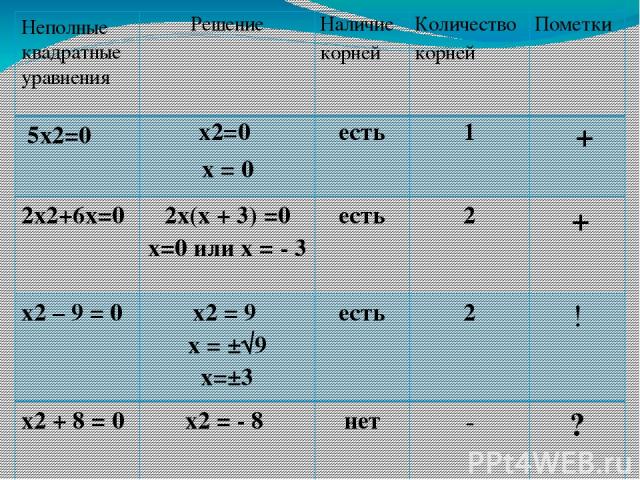
Неполные квадратные уравнения Решение Наличие корней Количество корней Пометки 5x2=0 x2=0 x = 0 есть 1    + 2x2+6x=0 2x(x +3) =0 x=0илиx = - 3 есть 2  + x2– 9= 0 x2=9 x = ±√9 x=±3 есть 2 ! x2+ 8= 0 x2= - 8 нет -  ?

зарядка

Ладошки складываем лодочкой и прикрываем глаза. При этом пальцы скрещиваются на переносице. Секунд 30 сидим так, представляя себе солнечное, летнее утро.

III. Стадия рефлексии (или размышления) - Возвращение к таблице(ее уточнение и дополнение с учетом того нового, что узнали) - Выполнение практического задания - Определение способов применения этой информации на практике

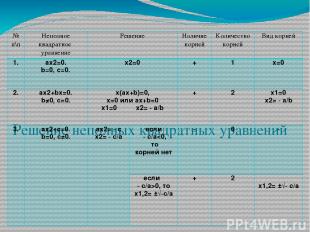
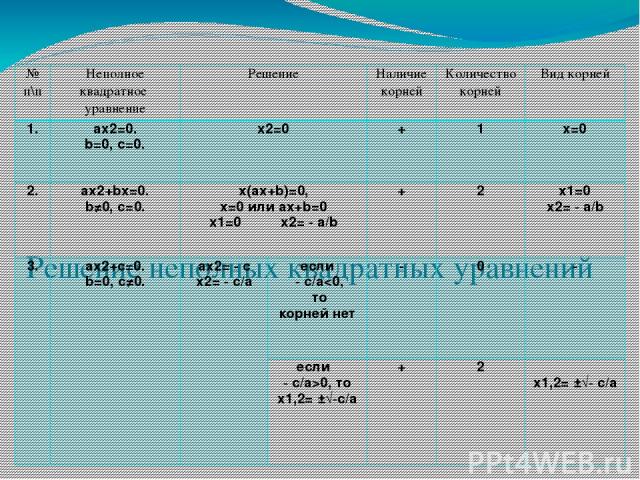
Решение неполных квадратных уравнений № п\п Неполное квадратное уравнение Решение Наличиекорней Количествокорней Видкорней 1. аx2=0. b=0, с=0. x2=0 + 1 x=0 2. ax2+bx=0. b≠0, с=0. x(ax+b)=0, x=0илиax+b=0 x1=0 x2=- a/b + 2 x1=0 x2= - a/b 3. ax2+c=0. b=0,с≠0. ax2= - c x2=- c/a если - c/a0,то x1,2=±√-c/a + 2 x1,2=±√- c/a

Разбейте следующие уравнения на две группы по какому-либо признаку: 1) 3х²+8х-7=0 7) 3х2– 5х – 4 =0 2) х2+ 3х+ 1 = 0 8) х2-24x= 0 3) 7-5х+х²=0 9) 16х2– 4 = 0 4) 5х2= 0 10) –0,1х2+ 10= 0 5) 169 –х2= 0 11)-x2– 3x+ 15 = 0 6) 7х + 13 -6х²=0 12) x2–5x = 0

Приведенные и неприведенные Приведенные х2 + 3х+ 1 = 0 7-5х+х²=0 Неприведенные 3х²+8х-7=0 - x2 – 3x + 15 = 0

Полные и неполные Полные 1) 3х²+8х-7=0 2) х2 + 3х+ 1 = 0 3) 7-5х+х²=0 7х + 13 -6х²=0 3х2 – 5х – 4 =0 - x2 – 3x + 15 = 0 Неполные 5х2 = 0 169 –х2 = 0 х2 - 24x = 0 16х2 – 4 = 0 – 0,1х2 + 10 = 0 x2 – 5x = 0

Проверка 1) 5х2 = 0 4) 16х2 – 4 = 0 2) 169 –х2 = 0 5) – 0,1х2 + 10 = 0 3) х2 - 24x = 0 6) x2 – 5x = 0 0 и 5 10 и -10 13 и -13 0 0,5 и -0,5 0 и 24 А К В Э И Р

Итог урока: “Эврика” крикнул Архимед, когда открыл известный вам закон. Что вы открыли для себя сегодня? Что вы узнали нового? Домашнее задание: п24; №24.4а), №24.8б), №24.9а), 24.12а), №24.16б), 24.18б), 24.20б)    

Литература: А.Г. Мордкович «Алгебра 8» учебник 1 часть А.Г. Мордкович «Алгебра 8»задачник 2 часть С.И. Заир-Бек, И.В. Муштавинская «Развитие критического мышления на уроке»