Презентация на тему: Математика в шахматах

Математика в шахматах "В шахматах я ценю прежде всего логику" Тигран Петросян(9-й чемпион мира)

Цель работы найти и разобрать связь между шахматами и математикой, воспользоваться этой связью при решении математических задач.

Задачи Найти связь между шахматами и математикой. Разобрать на примерах, в чём заключается эта связь. Сделать вывод.

Связь между шахматами и математикой Симметрия Система координат Геометрия Чётность, нечётность Решение задач

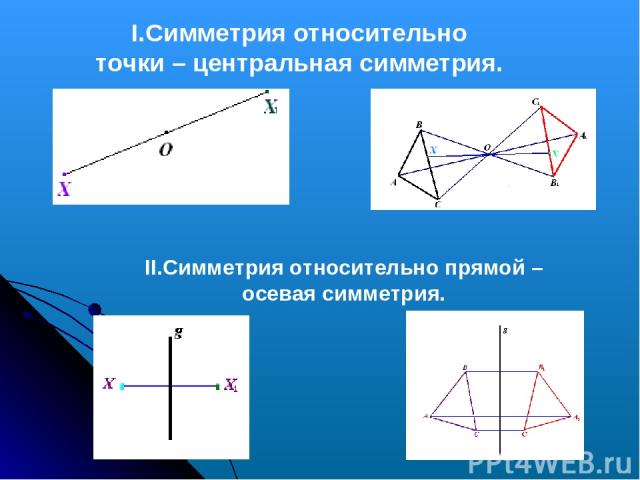
Симметрия в шахматах Симметрия бывает различных типов; наиболее распространены – осевая и центральная. На шахматной доске при осевой симметрии осью служит прямая, разделяющая левый и правый фланги доски (граница между вертикалями «d» и «e») или нижнюю и верхнею части). Если белый конь стоит на с2, а черный на с7, то эти кони расположены симметрично. Симметрия на шахматной доске

I.Симметрия относительно точки – центральная симметрия. II.Симметрия относительно прямой – осевая симметрия.

Система координат Система координат – это описание того, где расположен тот или иной объект(предмет, место). Так на билете в цирк номер ряда и номер места в ряду-координаты этого места, или а4;d3- координаты Ферзя на шахматном поле. Точка(с3) Эта точка может быть любой шахматной фигурой

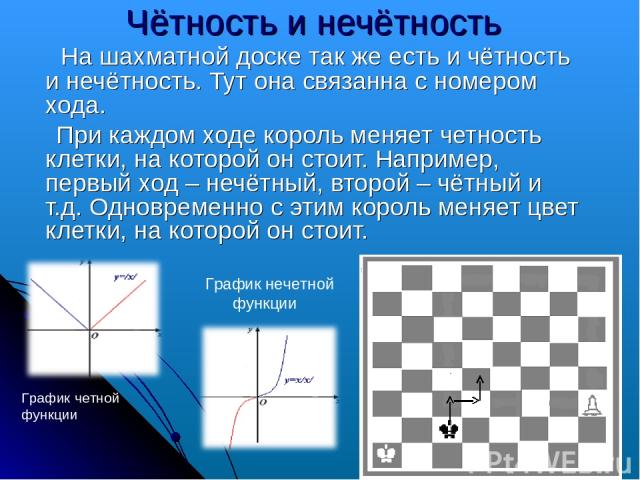
На шахматной доске так же есть и чётность и нечётность. Тут она связанна с номером хода. При каждом ходе король меняет четность клетки, на которой он стоит. Например, первый ход – нечётный, второй – чётный и т.д. Одновременно с этим король меняет цвет клетки, на которой он стоит. Чётность и нечётность График четной функции График нечетной функции

Геометрия шахматной доски Правило квадрата При этой композиции неопытные шахматисты рассуждают так: пешка идет сюда, король туда, пешка сюда, король туда и т.д. и при этом они часто путаются и в конце концов просчитываются. Однако исход игры легко оценить при помощи «правила квадрата».

Достаточно выяснить, может ли король при своем ходе попасть в квадрат пешки, - в данном случаи изображенном на рисунке. И так в нашей композиции черные при ходе делают ничью (попадают в квадрат), а при ходе противника проигрывают.

Задачи на четность, нечётность Конь вышел на поле А1 и через несколько ходов вернулся на него. Докажите, что он сделал четное число ходов. Вы наверное, заметили, что, делая каждый ход, конь меняет цвет клетки, на которой он стоит. Следовательно: каждый нечетный ход конь будет вставать на белую клетку. Исходя из этого конь должен вернуться на клетку А1, черного цвета. Мы можем сказать, что он вернется через четное число ходов.

Задачи Может ли конь пройти с поля a1 на поле h(8), побывав по дороге на каждом из остальных полей ровно один раз? Решение: Как и в предыдущем задании при каждом ходе конь меняет цвет клетки на которой он стоит. Следовательно, на доске 63 хода (нечетное число), h8 – черная клетка, при 62 ходе конь будет на белой клетке.

. Из шахматной доски 8*8 вырезали две противоположные угловые клетки. Докажите, что остаток доски нельзя разделить на доминошки (прямоугольники1*2). Решение: На шахматной доске, при удалении двух угловых клеток (а это либо две белых, либо две чёрных клетки), у нас получится 30 белых (чёрных) и 32 чёрных (белых) А это значит, что мы не сможем разделить оставшуюся часть доски на доминошки (так как неравное количество чёрных и белых клеток). задача

Теорема Пифагора на шахматной доске. Все мы знаем известную теорему Пифагора «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Эту теорему уже несколько сотен лет изучают школьники. С её помощью мы решаем задачи, инженеры строят дома. Так же теорема Пифагора широко используется в повседневной жизни.

Теорема Пифагора на шахматной доске Все мы знаем известную теорему Пифагора «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». С её помощью мы решаем задачи, инженеры строят дома. Так же теорема Пифагора используется на шахматной доске

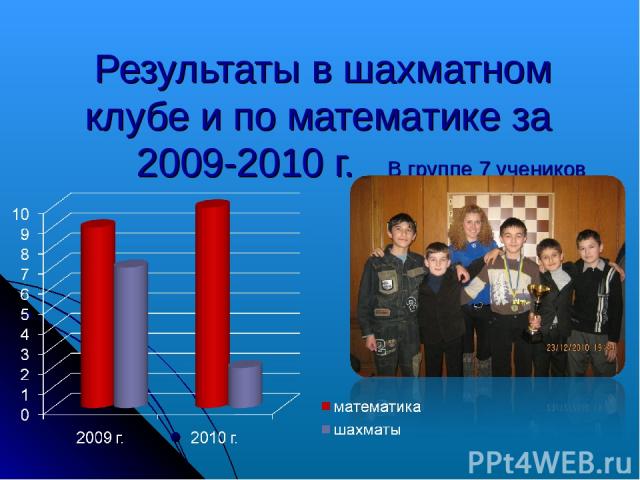
Результаты в шахматном клубе и по математике за 2009-2010 г. В группе 7 учеников

Математика помогает шахматистам играть и выигрывать. А шахматы в свою очередь помогают нам решать математические задачи, помогают развивать логику, внимание и таким образом знать математику. В начале работы мы поставили цель найти связь между шахматами и математикой, и считаю, что выполнили поставленную задачу. На примерах подробно разобрали эту связь. В дальнейшем, я разберу то, что осталось для меня загадкой и обязательно буду продолжать играть в шахматы, чтобы знать математику еще лучше.