Презентация на тему: Площадь треугольника и трапеции

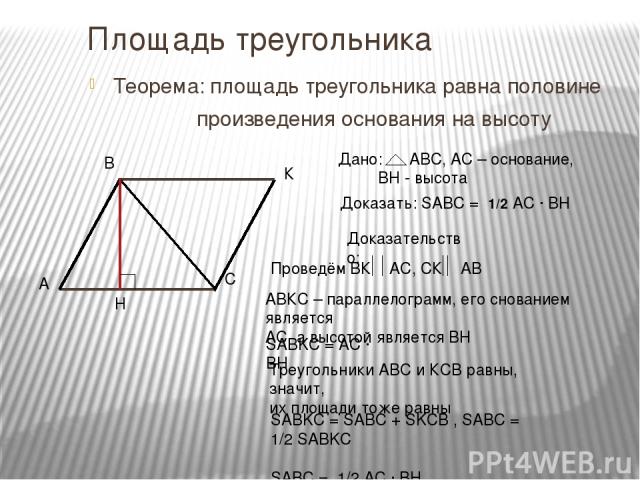
Площадь треугольника Теорема: площадь треугольника равна половине произведения основания на высоту Доказать: SABC = 1/2 AC ∙ BH Доказательство: АВКС – параллелограмм, его снованием является АС, а высотой является ВН SABKC = AC ∙ BH SABKC = SABC + SKCB , SABC = 1/2 SABKC SABC = 1/2 AC ∙ BH Треугольники АВС и КСВ равны, значит, их площади тоже равны К Дано: АВС, АС – основание, ВН - высота Проведём ВК АС, СК АВ

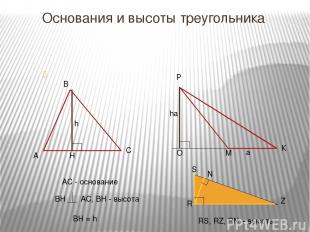
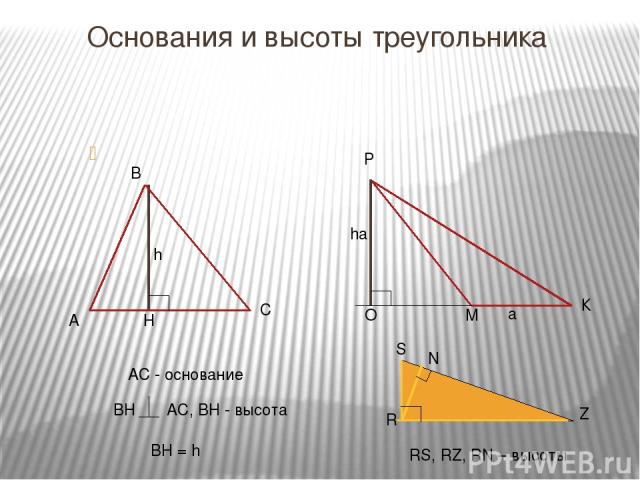
Основания и высоты треугольника АС - основание BH = h RS, RZ, RN – высоты

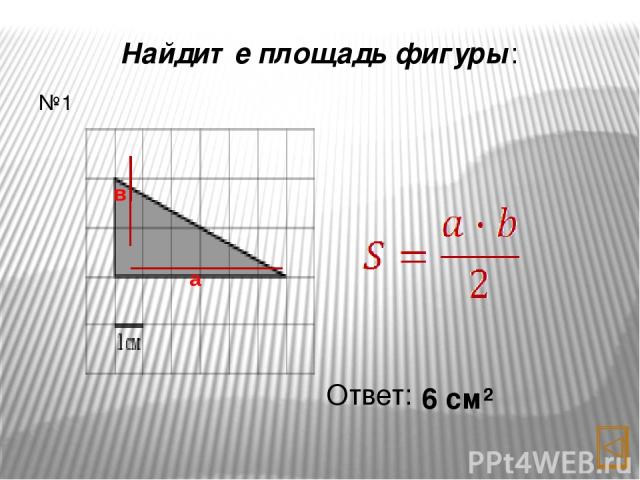
Найдите площадь фигуры: Ответ: 6 см² №1 а в

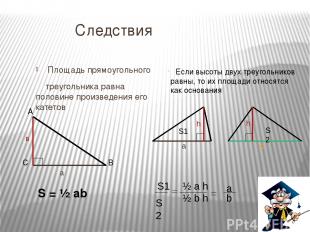
Площадь трапеции равна произведению полусуммы оснований на высоту S=½*(a+b)*h A B C D K h a b

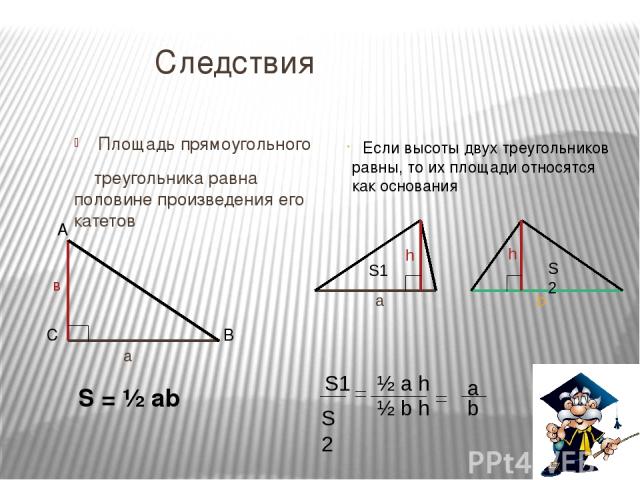
Следствия Площадь прямоугольного треугольника равна половине произведения его катетов S = ½ ab Если высоты двух треугольников равны, то их площади относятся как основания h a S1 h b S2 S1 S2 ½ a h ½ b h a b

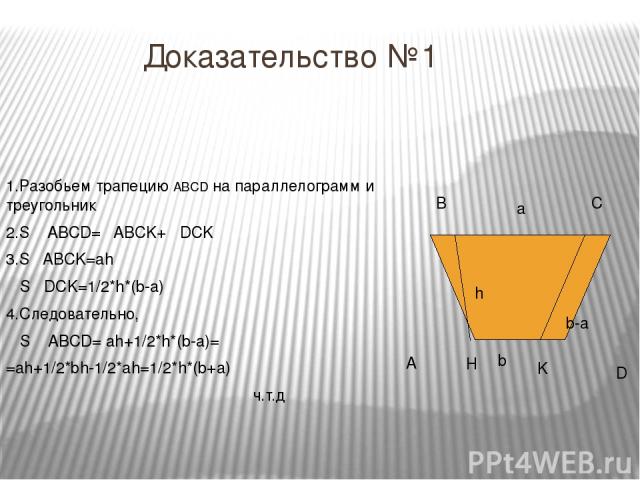
Доказательство №1 A B C D H h b-a K a b 1.Разобьем трапецию ABCD на параллелограмм и треугольник 2.S ABCD= ABCK+ DCK 3.S ABCK=ah S DCK=1/2*h*(b-a) 4.Следовательно, S ABCD= ah+1/2*h*(b-a)= =ah+1/2*bh-1/2*ah=1/2*h*(b+a) ч.т.д

Доказательство №2 A B C D K E b-a a b h 1.Достроим трапецию ABCD до параллелограмма ABED и проведем высоту h 2.S ABCD= S ABED- S CED S CED=1/2*h*(b-a) 3. S ABED=bh 4.Следовательно, S ABED=bh-1/2*h*(b-a)=bh-- 1/2*bh+1/2*ah=1/2*ah+1/2*bh=1/2*h*(a+b).

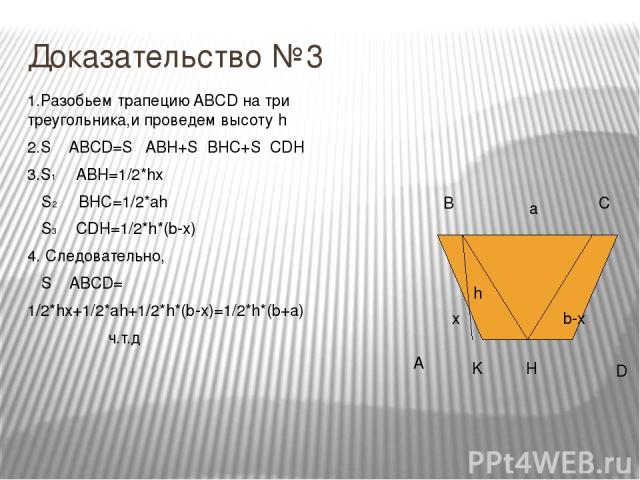
Доказательство №3 A B C D x h b-x K H a 1.Разобьем трапецию ABCD на три треугольника,и проведем высоту h 2.S ABCD=S ABH+S BHC+S CDH 3.S1 ABH=1/2*hx S2 BHC=1/2*ah S3 CDH=1/2*h*(b-x) 4. Следовательно, S ABCD= 1/2*hx+1/2*ah+1/2*h*(b-x)=1/2*h*(b+a) ч.т.д

Доказательство №5 A B C D h a b K 1.Разобьем трапецию ABCD на два треугольника и проведем высоту h на основание AD 2.S ABCD= S BDK+S BCD S BCD=1/2*ah S BDK=1/2*bh 3.Слеовательно, S ABCD=1/2*ah+1/2*bh=1/2*h*(b+a) ч.т.д

Доказательство №6 A B C D 1.Разобьем трапецию ABCD на прямоугольник и два треугольника 2.Докажем,что Sтрапеции равна произведению полусуммы ее оснований на высоту 3. a)S ABH=1/2xh б)S DCK=1/2h(b-a-x) с)S HBCK=ah 4. Следовательно, S ABCD=1/2xh+1/2h(b-a-x)+ah= ½h(x+b-a-x)+ah=1/2h(b-a)+ah= =1/2(a+b)h. ч.т.д K a b b-a-x x H

Вычисление площадей фигур на клетчатой бумаге 1 2 3 4 5 6 7 8 9 10 11 12

Найдите площадь фигуры: Ответ: 12 см² №3 a h

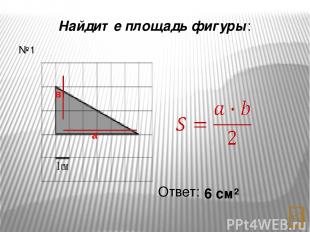
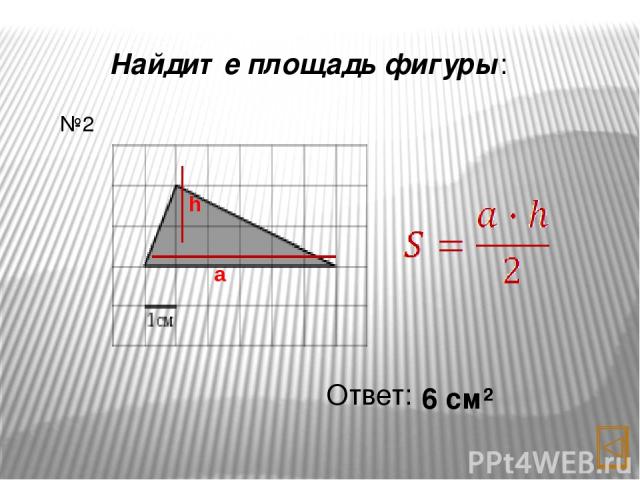
Найдите площадь фигуры: Ответ: 6 см² №2 а h

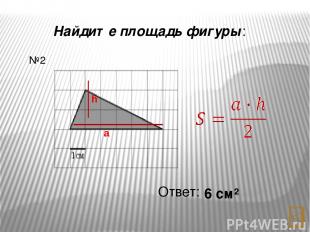
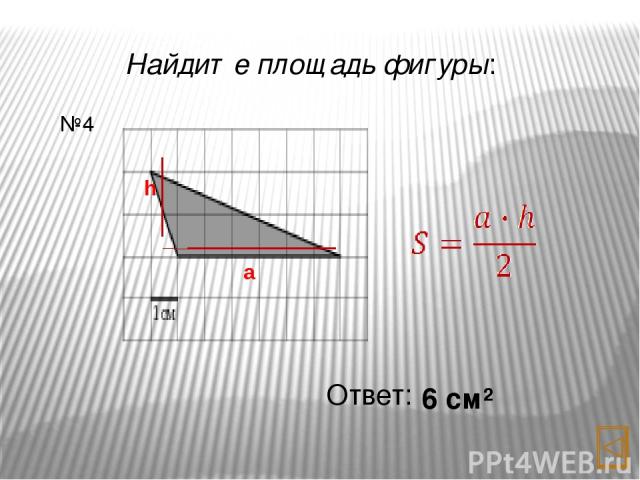
Найдите площадь фигуры: Ответ: 6 см² №4 a h

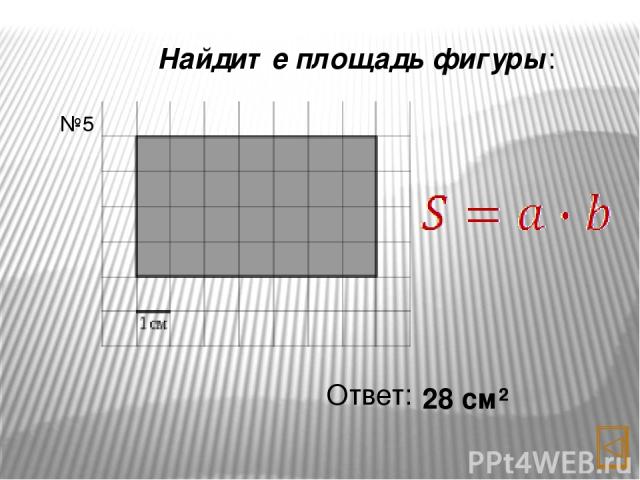
Найдите площадь фигуры: Ответ: 28 см² №5

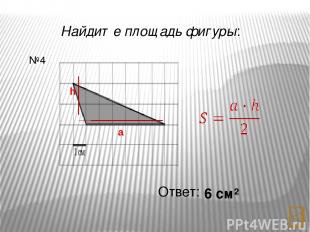
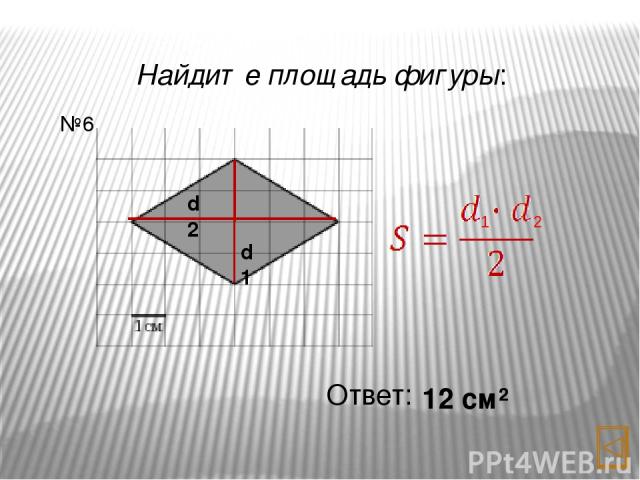
Найдите площадь фигуры: Ответ: 12 см² №6 d1 d2 1 2

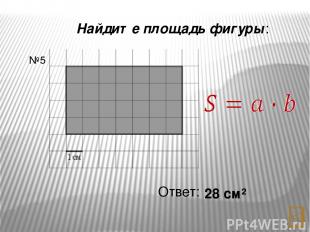
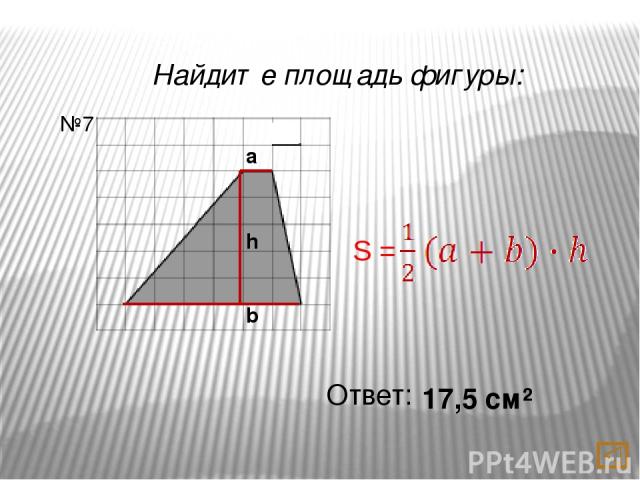
Найдите площадь фигуры: Ответ: 17,5 см² №7 a b h S =

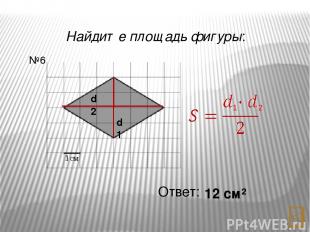
Найдите площадь фигуры: Ответ: 32, 5 см² №8 a h b

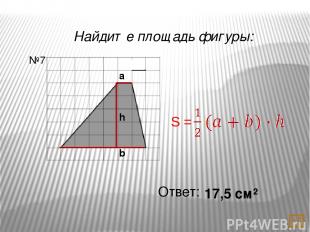
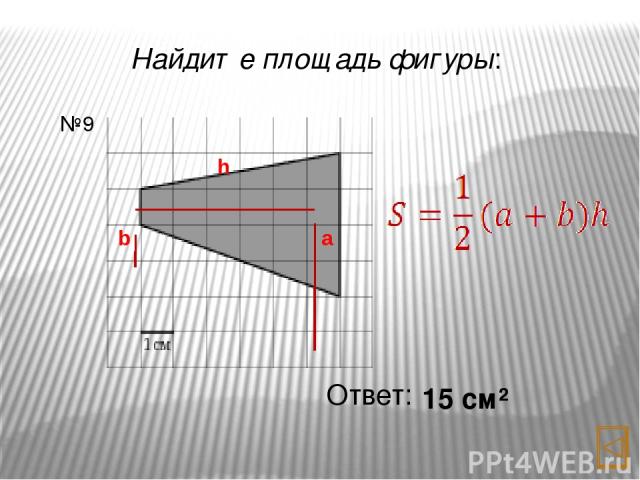
Найдите площадь фигуры: Ответ: 15 см² №9 a h b

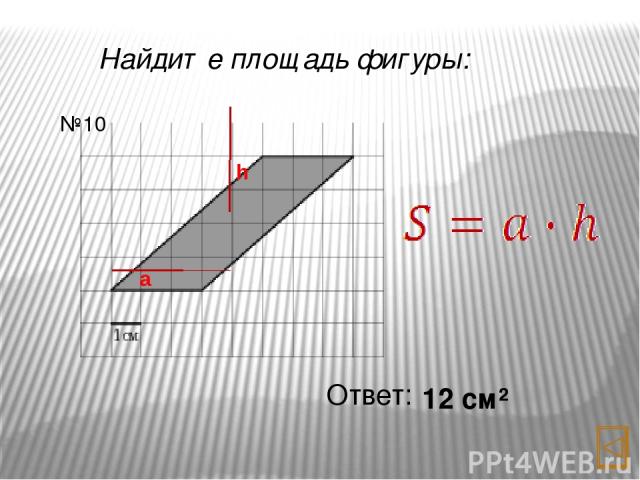
Найдите площадь фигуры: Ответ: 12 см² №10 a h

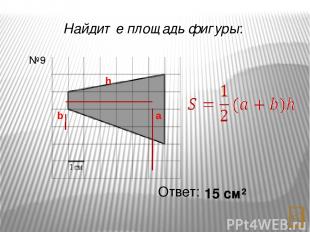
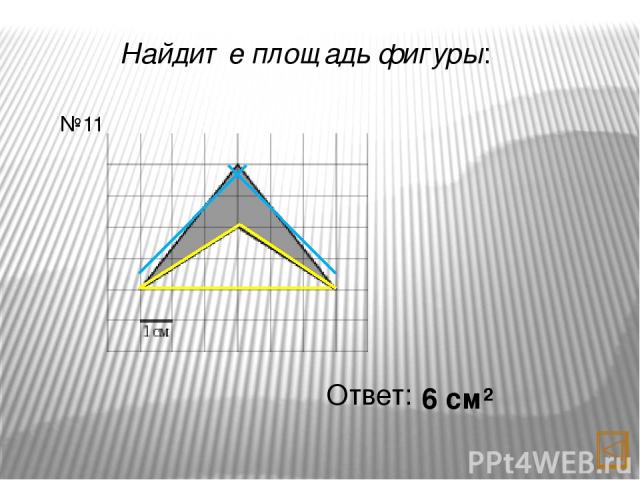
Найдите площадь фигуры: Ответ: 6 см² №11

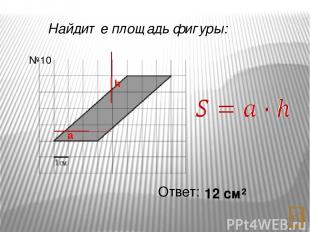
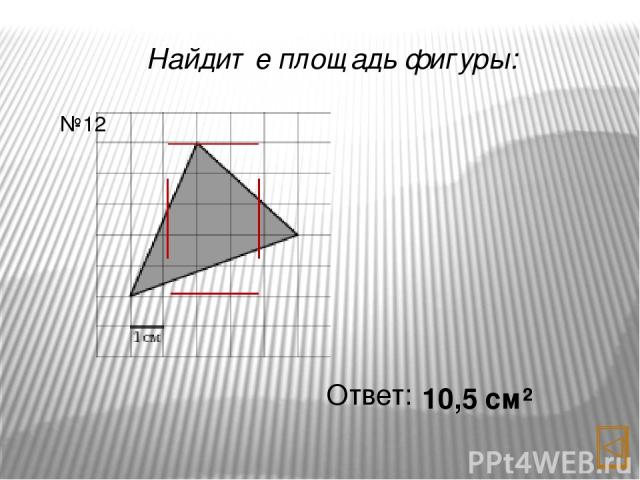
Найдите площадь фигуры: Ответ: 10,5 см² №12

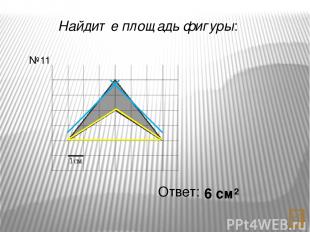
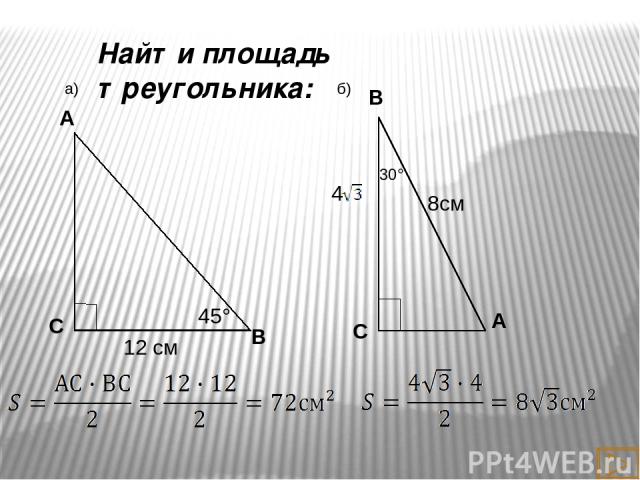
Найти площадь треугольника: С а)

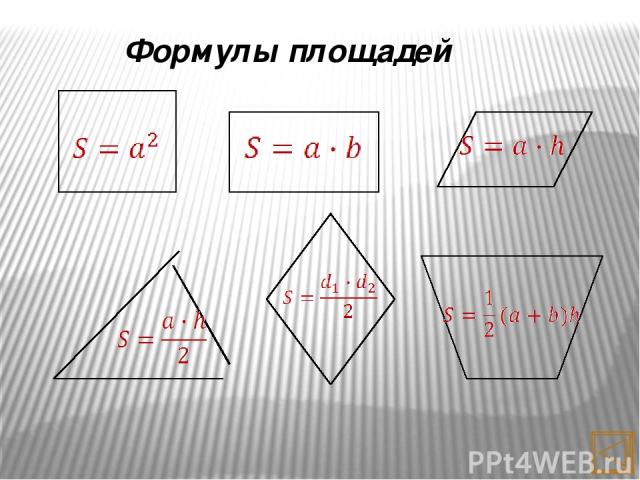
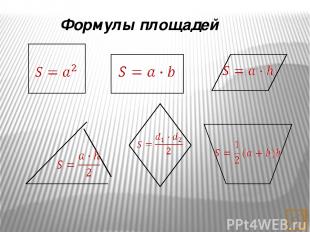
Формулы площадей

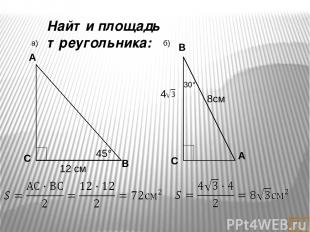
1. В треугольнике АВС С = 135 , АС = 6 дм, высота ВД равна 2 дм. Найти площадь треугольника АВД. Решение: АВД- прямоугольный ВСД – прямоугольный, ВСД = 180 -135 = 45 СВД =45 ВСД- равнобедренный, СД = ВД = =2 дм АД = АС + СД = 8 дм Ответ: 8дм² А Д В С

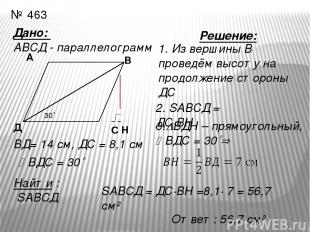
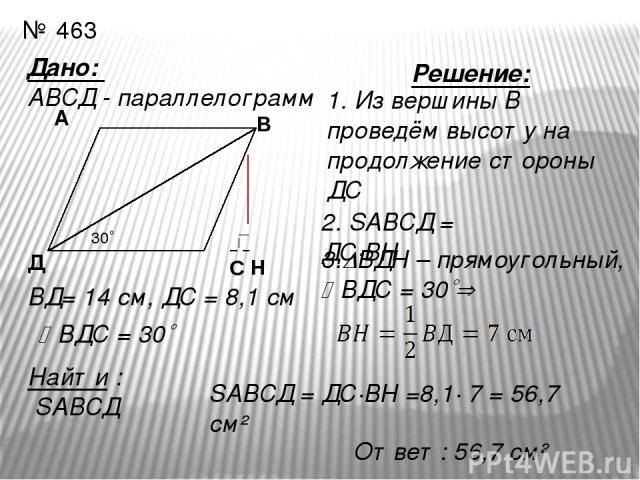
№ 463 Дано: АВСД - параллелограмм Д А ВД= 14 см, ДС = 8,1 см ВДС = 30 Найти : SАВСД 30 Решение: 1. Из вершины В проведём высоту на продолжение стороны ДС 2. SАВСД = ДС∙ВН 3. ВДН – прямоугольный, ВДС = 30 SАВСД = ДС∙ВН =8,1∙ 7 = 56,7 см² Ответ: 56,7 см² Н С В

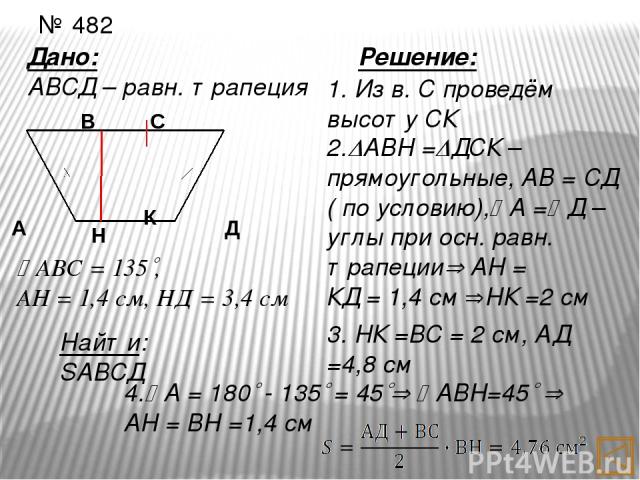
№ 482 Дано: АВСД – равн. трапеция Найти: SАВСД Решение: 1. Из в. С проведём высоту СК 2. АВН = ДСК – прямоугольные, АВ = СД ( по условию), А = Д – углы при осн. равн. трапеции АН = КД = 1,4 см НК =2 см 3. НК =ВС = 2 см, АД =4,8 см 4. А = 180 - 135 = 45 АВН=45 АН = ВН =1,4 см А Н Д С В АВС = 135 , АН = 1,4 см, НД = 3,4 см К