Презентация на тему: Преобразование графиков функции

Тема:«Преобразование графиков функции»

Цели: 1)Систематизировать приемы построения графиков.2)Показать их применение при построении:а) графиков сложных функций;б) при решении заданий ЕГЭ из части C.

Рассмотрим основные правила преобразования графиков на примерах элементарных функций
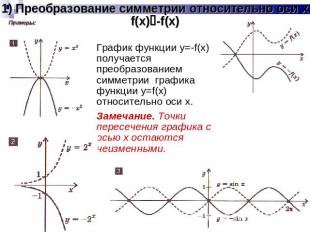
1) Преобразование симметрии относительно оси xf(x)-f(x) График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.Замечание. Точки пересечения графика с осью x остаются неизменными.
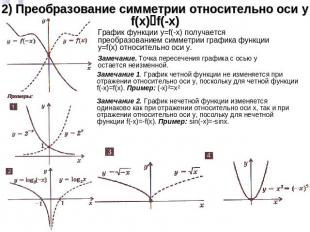
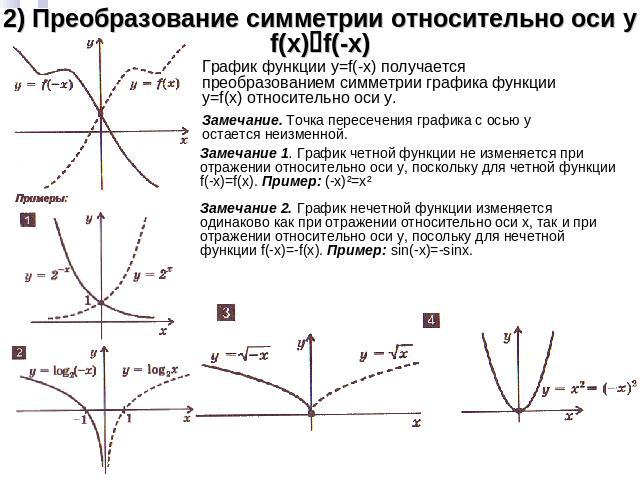
2) Преобразование симметрии относительно оси yf(x)f(-x) График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.Замечание. Точка пересечения графика с осью y остается неизменной.Замечание 1. График четной функции не изменяется при отражении относительно оси y, поскольку для четной функции f(-x)=f(x). Пример: (-x)²=x²Замечание 2. График нечетной функции изменяется одинаково как при отражении относительно оси x, так и при отражении относительно оси y, посольку для нечетной функции f(-x)=-f(x). Пример: sin(-x)=-sinx.
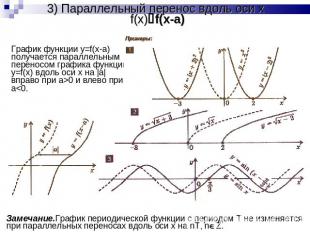
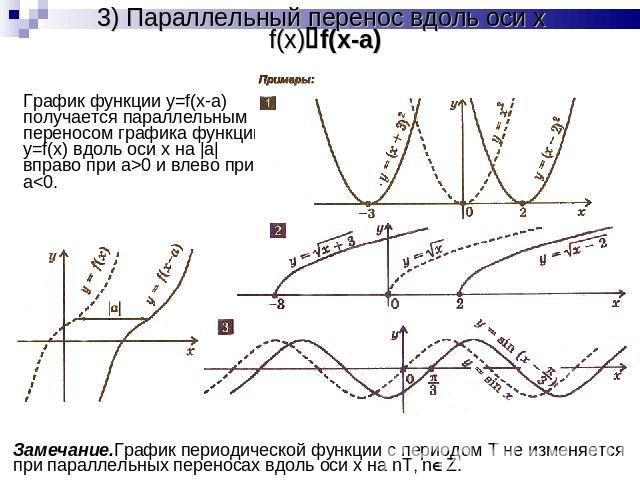
3) Параллельный перенос вдоль оси x f(x)f(x-a) График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.Замечание.График периодической функции с периодом T не изменяется при параллельных переносах вдоль оси x на nT, nZ.
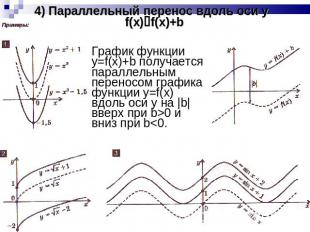
4) Параллельный перенос вдоль оси y f(x)f(x)+b График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.
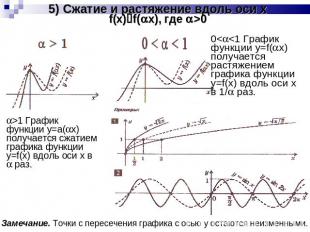
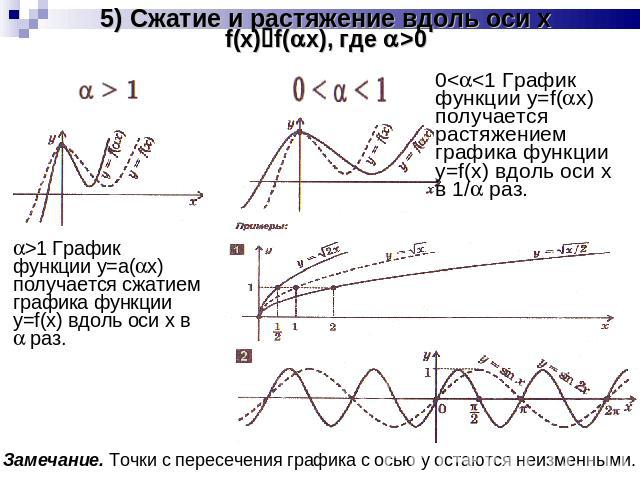
5) Сжатие и растяжение вдоль оси xf(x)f(x), где >0 0<<1 График функции y=f(x) получается растяжением графика функции y=f(x) вдоль оси x в 1/ раз.>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в раз.Замечание. Точки с пересечения графика с осью y остаются неизменными.
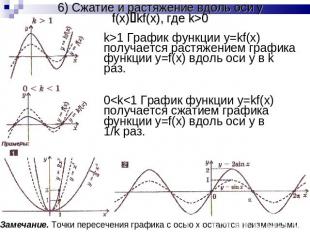
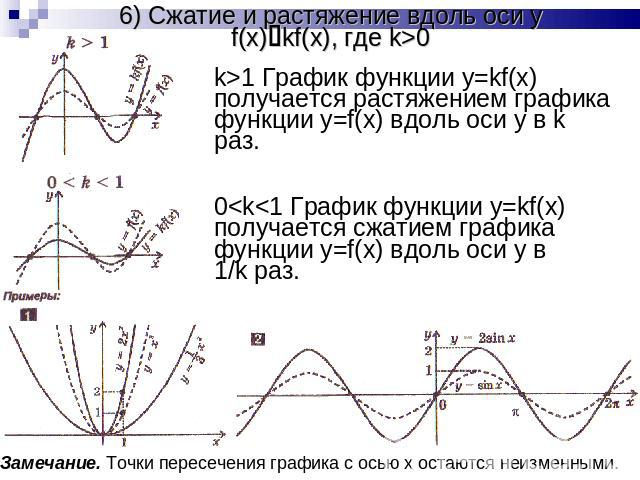
6) Сжатие и растяжение вдоль оси yf(x)kf(x), где k>0 k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.0<k<1 График функции y=kf(x) получается сжатием графика функции y=f(x) вдоль оси y в 1/k раз.Замечание. Точки пересечения графика с осью x остаются неизменными.
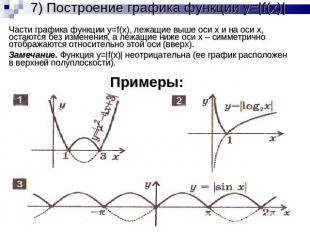
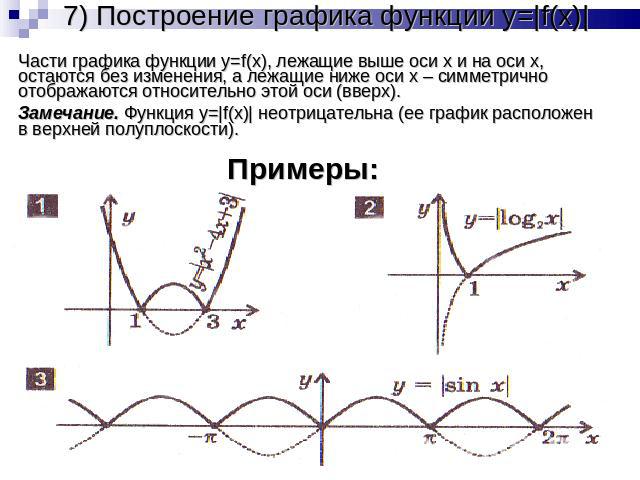
7) Построение графика функции y=|f(x)| Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).
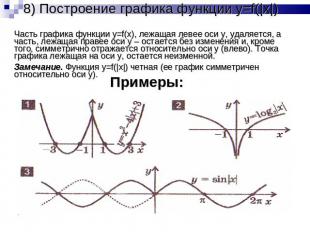
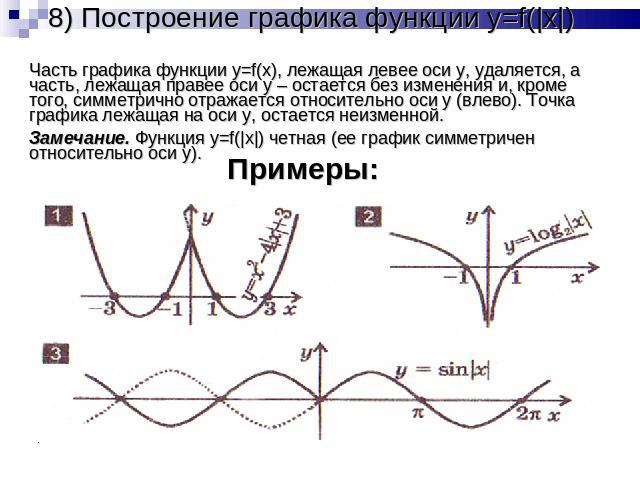
8) Построение графика функции y=f(|x|) Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).
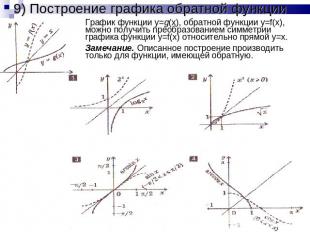
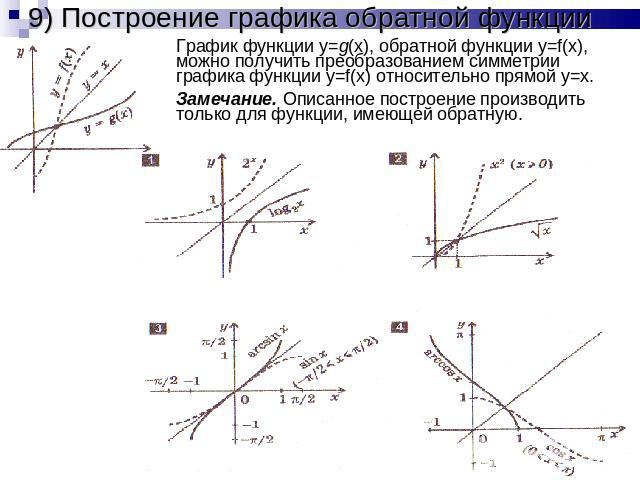
9) Построение графика обратной функции График функции y=g(x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.Замечание. Описанное построение производить только для функции, имеющей обратную.

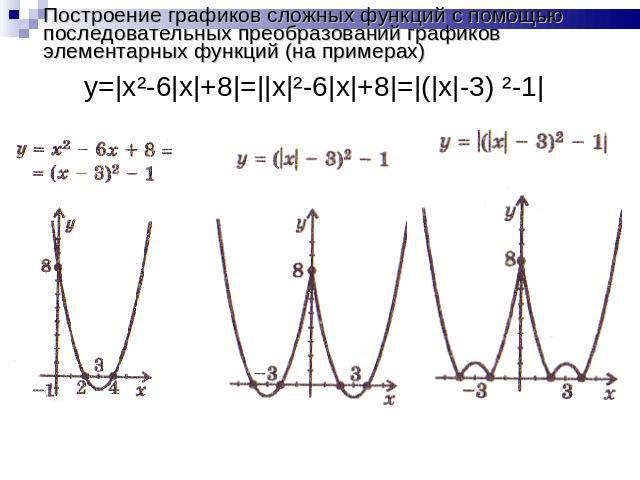
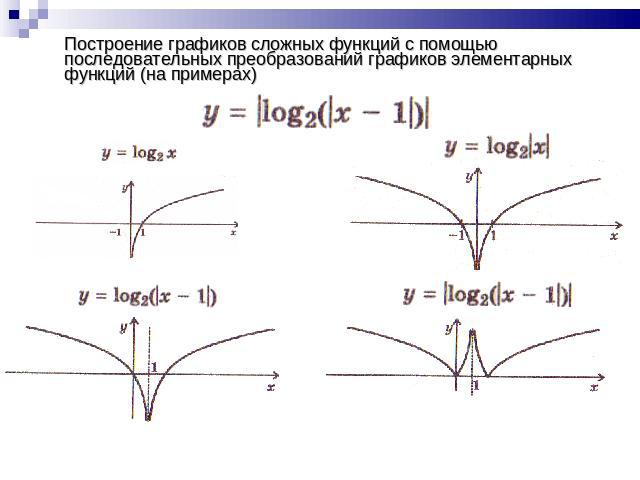
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
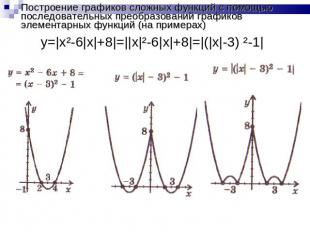
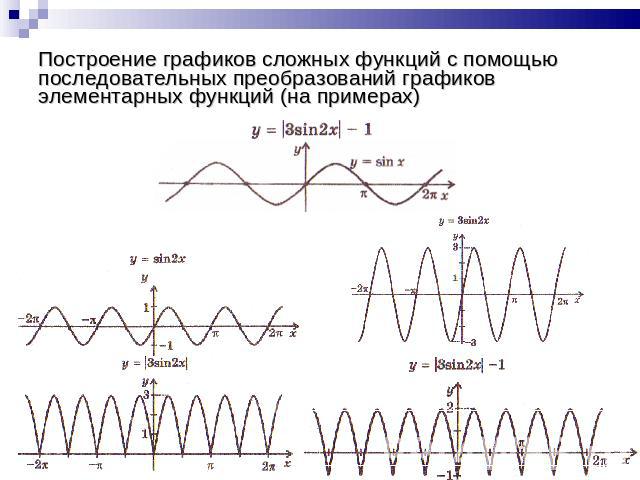
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
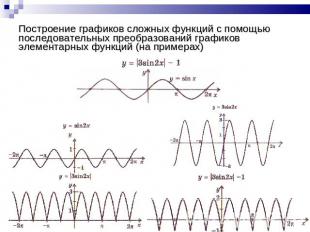
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Применение правил преобразования графиков при решении заданий ЕГЭ(части C).
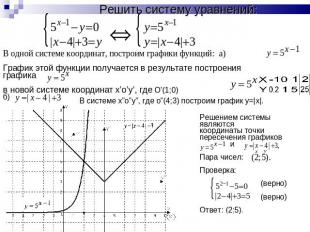
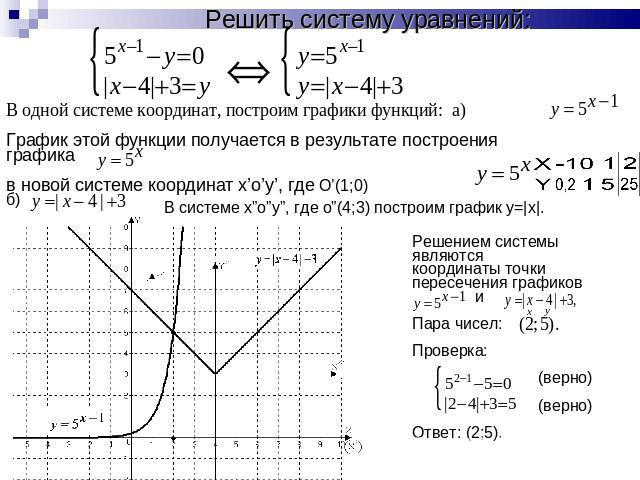
В одной системе координат, построим графики функций: а) График этой функции получается в результате построения графика в новой системе координат x’o’y’, где O’(1;0) б)Решением системы являются координаты точки пересечения графиков иПара чисел:Проверка: (верно) (верно)Ответ: (2;5).

Решение: Преобразуем функцию f(x).Так как , тоТогда g(f(x))=20.Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32; f(g(x))=12Пусть g(x)=t, тогда f(t)=12 или Имеем: g(x)=0 или g(x)=4Так как при x≥5 g(x)=20, то решения уравнений: g(x)=0 и g(x)=4 будем искать среди x<5.Тогда: а) Уравнение g(x)=0 примет вид:Так как x<5, то 6-x>0 Вывод: уравнение g(x)=0 не имеет корней.б) уравнение g(x)=4 примет вид:В одной системе координат построим графики функций и
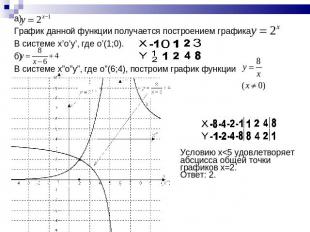
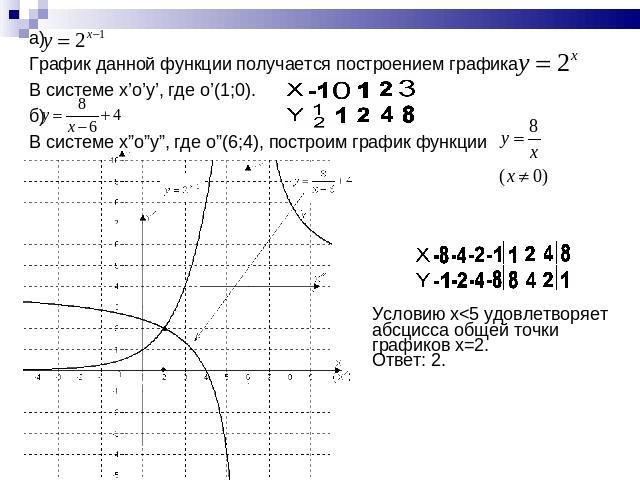
а) График данной функции получается построением графикаВ системе x’o’y’, где o’(1;0).б) В системе x”o”y”, где o”(6;4), построим график функции Условию x<5 удовлетворяет абсцисса общей точки графиков x=2. Ответ: 2.

Вывод: Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций. Помогают найти нетрадиционное решение сложных задач.

Тема:«Преобразование графиков функции»