Презентация на тему: Быстрое преобразование Фурье

Лекция № 12 Быстрое преобразование Фурье Нахождение спектральных составляющих дискретного комплексного сигнала непосредственно по формуле ДПФ требует комплексных умножений и комплексных сложений. Так как количество вычислений, а следовательно, и время вычислений приблизительно пропорциональны , то при больших количество арифметических операций весьма велико. Поэтому нахождение спектра в реальном времени даже для современной вычислительной техники представляет сложную задачу. По этой причине представляет значительный интерес вычислительные процедуры, уменьшающие количество умножений и сложений.

Быстрое преобразование Фурье Основной принцип всех этих алгоритмов заключается в разложении операций вычисления ДПФ сигнала длины на вычисление преобразований Фурье с меньшим числом точек. Разделив анализируемый набор отсчетов на части, вычисляют их ДПФ и объединяют результаты. Такие процедуры получили название алгоритмов быстрого преобразования Фурье БПФ.При реализации БПФ возможно несколько вариантов организации вычислений в зависимости от способа деления последовательности отсчетов на части (прореживание по времени или по частоте) и от того, на сколько фрагментов производится разбиение последовательности на каждом шаге (основание БПФ).

Быстрое преобразование Фурье Рассмотрим алгоритмы БПФ с основанием 2, когда длина последовательности , где целое число. БПФ с прореживанием по времени. Рассмотрим идею БПФ с прореживанием по времени на примере деления набора отсчетов пополам. Введя общепринятое в литературе обозначение для дискретных экспоненциальных функций: Запишем ДПФ сигнала в виде:

Быстрое преобразование Фурье Разобьем на две -точечные последовательности, состоящие из отсчетов с четными и нечетными номерами соответственно. В результате получим:Заменяя индексы суммирования на при четном и на при нечетном , придем к выражению:

Быстрое преобразование Фурье Так как , то предыдущее выражение можно записать в виде: (12.1)Каждая из сумм (12.1) является точечным ДПФ: первая – для четных отсчетов исходной последовательности, а вторая – для нечетных. Несмотря на то, что индекс в формуле (12.1) распространяется на значений , каждая из сумм требует вычислений только для , так как и периодичны по с периодом . Объединение же этих сумм приводит к точечному ДПФ .

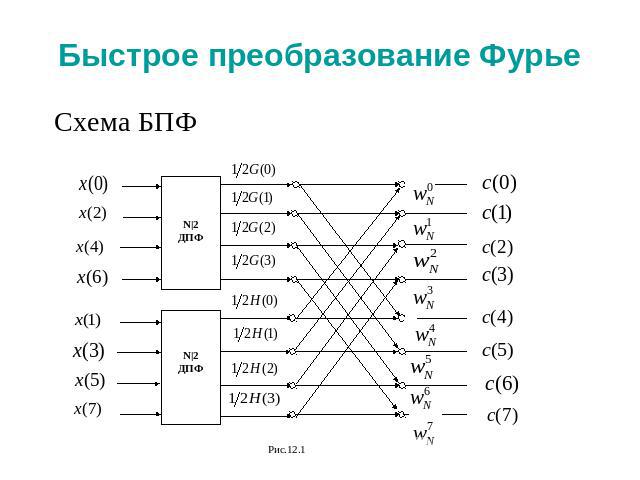
Быстрое преобразование Фурье Схема БПФ

Быстрое преобразование Фурье Далее можно вычислить каждое точечное ДПФ разбиением сумм на два точечных ДПФ. Таким образом, и могут быть вычислены в виде:

Быстрое преобразование Фурье Продолжим описанную процедуру разбиения исходной ДПФ на преобразования меньшей размерности, пока не останутся только двухточечные преобразования. Двухточечные ДПФ (их число равно ) могут быть вообще вычислены без использования операций умножения. Действительно, для двухточечной последовательности согласно определению ДПФ имеем два спектральных отсчета:

Быстрое преобразование Фурье Число требуемых при этом пар операций «умножение – сложение» можно оценить как . Таким образом, вычислительные затраты по сравнению с непосредственным использованием формулы ДПФ уменьшается в раз. При больших это отношение становится весьма велико. Например, при достигается более чем 100-кратное ускорение, но и это еще не предел. Количество комплексных умножений в алгоритме БПФ с прореживанием по времени может быть сокращено вдвое.

Быстрое преобразование Фурье Из рассмотренного алгоритма следует, что на каждой ступени вычислений происходит преобразование одного множества из комплексных чисел в другое множество из комплексных чисел. Будем считать входным массивом на ступени вычисления , а – выходным массивом на ступени вычислений. С учетом введенных обозначений имеем:

Быстрое преобразование Фурье Вышеприведенные соотношения подсказывают метод сокращения числа комплексных умножений вдвое. Так как , эти соотношения можно записать в виде:Так как на каждую ступень разбиения имеется таких операций, а общее число ступеней равно , то общее число пар операций «умножение-сложение» сокращается до .