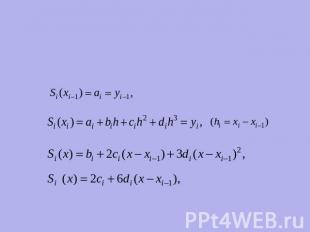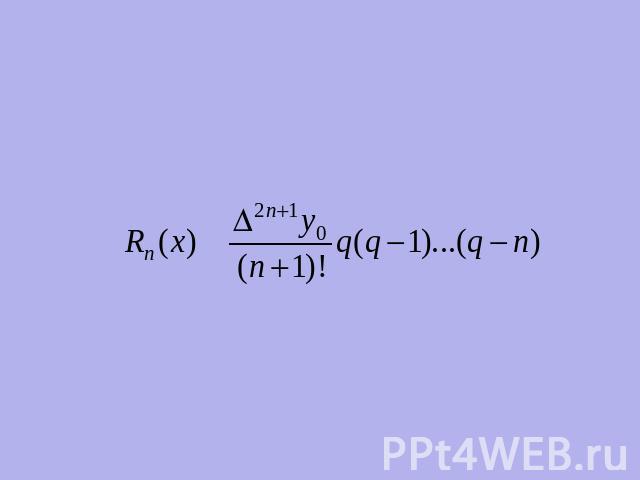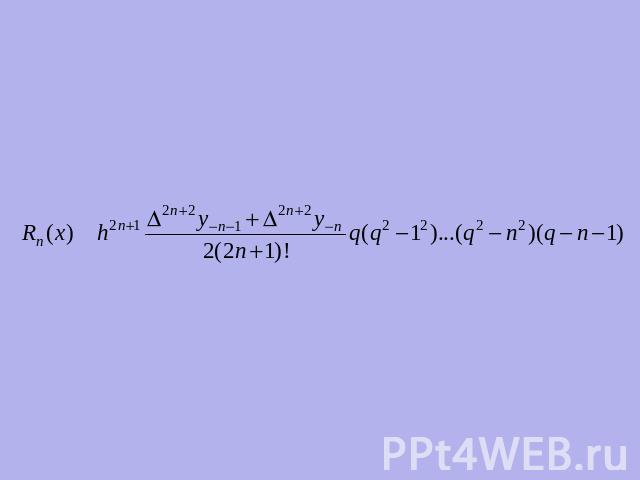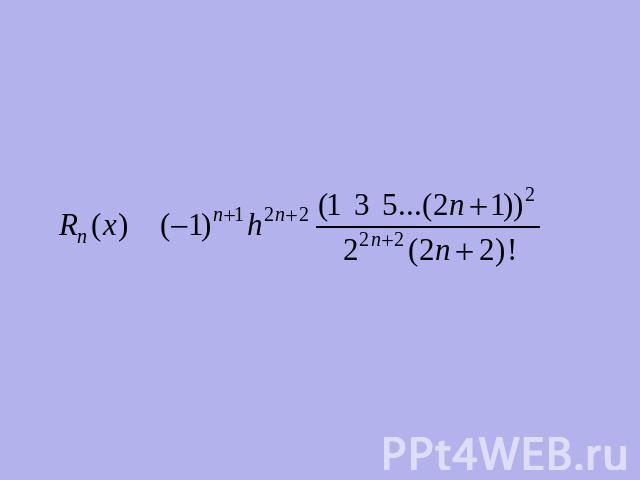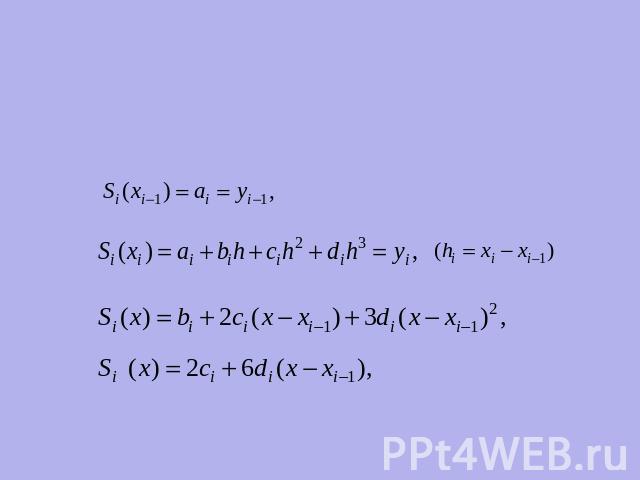Презентация на тему: Интерполяционные формулы

Интерполяционные формулы

Пусть точка х лежит в окрестности середины интервала содержащего 2n+1 равноотстоящих с шагом h узла интерполирования

Для интерполирования функции f(x) в этой точке можно использовать первой (х0<x) или второй (x0>x) интерполяционными формулами Гаусса.Обозначим

Первая интерполяционная формула Гаусса имеет вид:

Вторая интерполяционная формула Гаусса имеет вид:
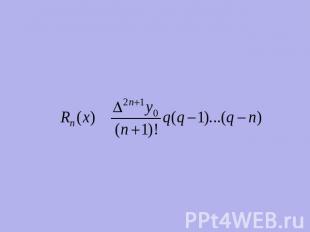

Формула Стирлинга представляет собой среднее арифметическое первой и второй интерполяционных формул Гаусса:


Формула Бесселя имеет вид:


Формула Стирлинга применяется для интерполирования при значениях q, близких к 0. на практике ее используют при

Формула Бесселя используется для интерполирования при значениях q, близких к 0,5. Практически она используется при

В том случае, когда q = 0.5, формула Бесселя может быть переписана в виде:- формула интерполирования на середину.
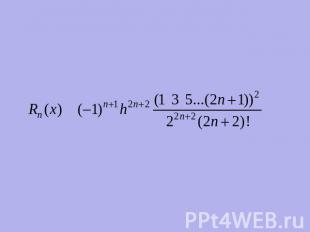

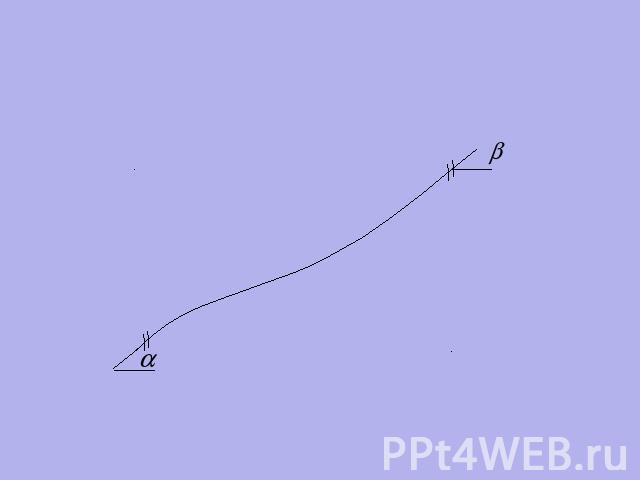
Сплайны. кубические сплайн-функции — это специальным образом построенные многочлены третьей степени.

Они представляют собой некоторую математическую модель гибкого тонкого стержня. Если закрепить его в двух соседних узлах интерполяции с заданными углами наклонов, то между точками закрепления этот стержень примет некоторую форму.

Пусть форма этого стержня определяется функциеймежду каждой парой соседних узлов интерполяции функция S(х) является многочленом степени не выше третьей.

Запишем ее в виде

Для определения коэффициентов на всех элементарных отрезках необходимо получить 4n уравнений.