Презентация на тему: Дисперсионный анализ

Дисперсионный анализ Докладчик: ординатор Хамаева А.А.

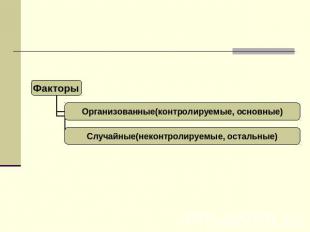
Основные понятия дисперсионного анализа Факторы – любые воздействия или состояния, определяющие ту или иную величину наблюдаемого признака Результативные признаки – наблюдаемые признаки, которые испытывают влияние изучаемых факторовВарианты – отдельные значения результативного признака

Статистические комплексы (таблицы) Равномерные – с одинаковым числом значений в каждой клетке комбинационной таблицыПропорциональные – число значений в различных клетках комбинационной таблицы различно, но соблюдена единая для всего комплекса пропорциональность между ними Непропорциональные – распределение значений по клеткам таблицы различно

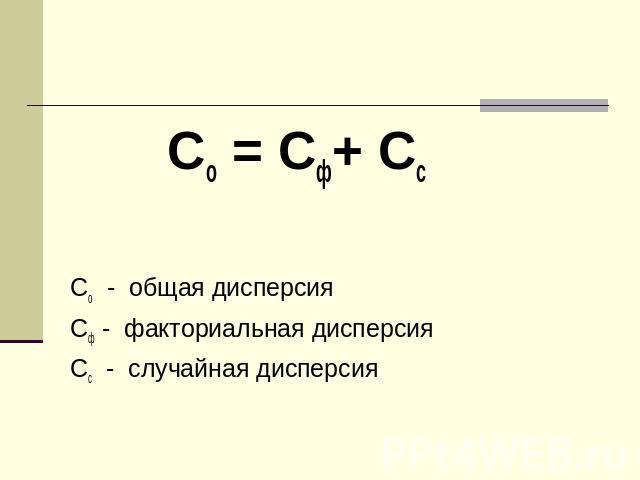
Общая дисперсия равна сумме дисперсий, вызванной организованными факторами(факториальной дисперсии) и дисперсии, вызванной случайными факторами(остаточной дисперсии)

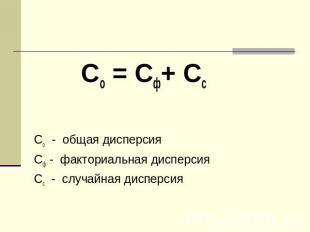
Со = Сф+ Сс Со - общая дисперсияСф - факториальная дисперсияСс - случайная дисперсия

Общая дисперсия: Факториальная дисперсия:Случайная дисперсия:Где Х – отдельное значение результативного признакаХс – общая средняя арифметическая всего комплексаХф – групповая средняя

Когда измеряется влияние нескольких факторов (в многофакторном комплексе), сумма дисперсий каждого из учитываемых факторов и случайной дисперсии должна быть равна общей дисперсии: Со = Сф1 + Сф2 + Сф3 + … + Сфn + Сc

Доля участия отдельных факторов в формировании результативного признака определяется из отношения групповых дисперсий к общей (в процентах):

Для определения достоверностм влияния факторов в группах с разным числом значений применяется тка называемая девиата, т.е. дисперсия, приходящаяся на один элемент свободного варьирования или на одну степень свободы

При вычислении общей девиаты: ДО= СО / nПри вычислении факториальной девиаты: ДФ = CФ / nПри вычислении случайной девиаты: ДС = СС / n

Обработка однофакторного дисперсионного комплекса

Вычисление общей дисперсииСумма всех значений 54+57+73+70+67+63=384Число значений n=2х3=6Общая средняя х= 384/6=64Общая дисперсия (сумма квадратов отклонений каждого значения от общей средней) С = (54-64)2 +(57-64)2 +(73-64)2 +(67-64)2 +(63-64)2 =276

Вычисление факториальной (групповой) дисперсии Определить средние величины результативного признака каждой градации фактора (Хф)Вычесть из них общую среднюю всего комплекса (Х – Хс) и возвести в квадрат полученные отклоненияУмножить их на повторность опыта p*(Хф – Хо)2 и сложить эти произведения

Вычисление случайной дисперсии Находятся групповые средние (Хф)Определяются отклонения каждой даты от своей групповой средней (v – Хф) и полученные отклонения возводятся в квадратКвадраты отклонений складываются

Отношение факториальной дисперсии к общей характеризует степень влияния изучаемого фактора: Сф/Со = 259 / 276=0,94 Следовательно, статистическое влияние организованных факторов на результативный признак составляет 94%Степень влияния неучтенных факторов: Сс/Со = 17/276 = 0,06 Доля влияния на результативный признак неучтенных факторов составляет 6%

Оценка достоверности влияния организованных и неучтенных факторов на величину результативного признака производится путем сравнения отношения факториальной и случайной девиат с соответствующими табличными значениями

Число степеней свободы в однофакторном комплексе определяется следующим образом:Для общей дисперсии nо = n – 1, в примере 6 – 1 = 5Для факториальной дисперсии nф = r – 1, в примере 3 – 1 = 2Для случайной дисперсии nс = n – r , в примере 6 – 3 = 3

Обработка двухфакторного дисперсионного комплекса 1. Вычисление общей дисперсии осуществляется как при однофакторном комплексе 2. Вычисление случайной дисперсии аналогично нахождению ее в однофакторном комплексе 3. Вычисление дисперсии суммарного действия организованных факторов

Двухфакторный статистический комплекс

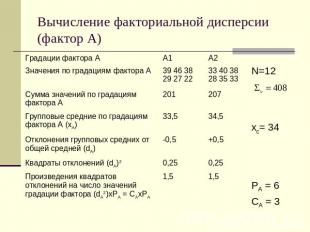
Вычисление факториальной дисперсии (фактор А)

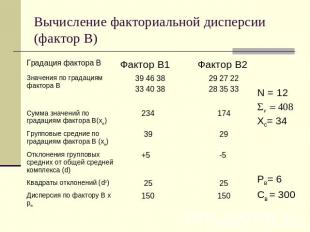
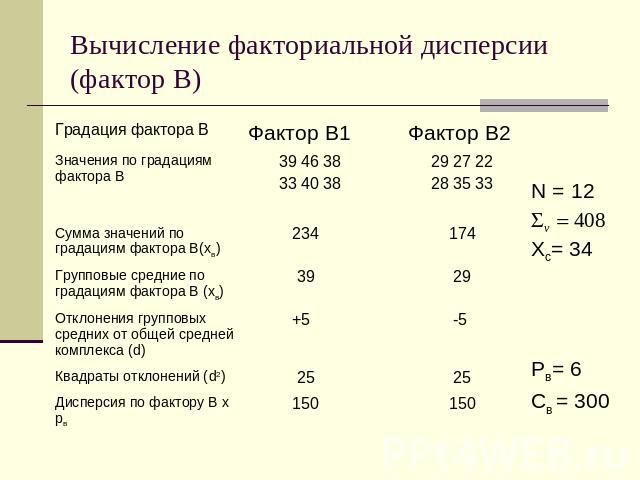
Вычисление факториальной дисперсии (фактор В)

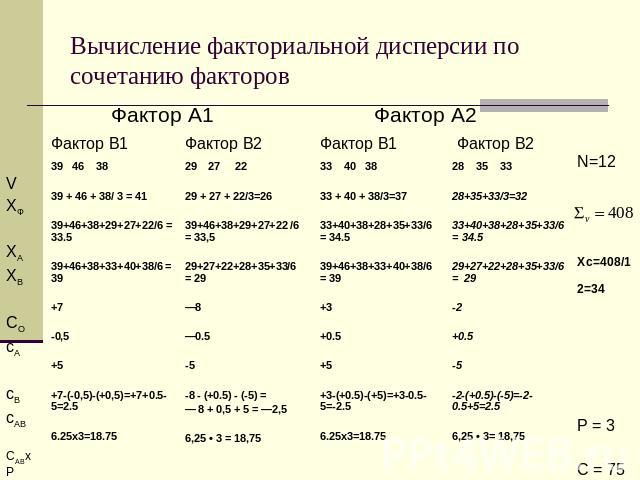
Вычисление факториальной дисперсии по сочетанию факторов

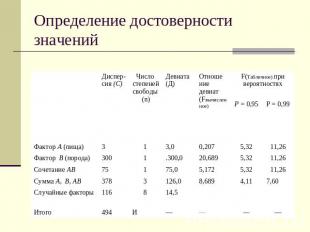
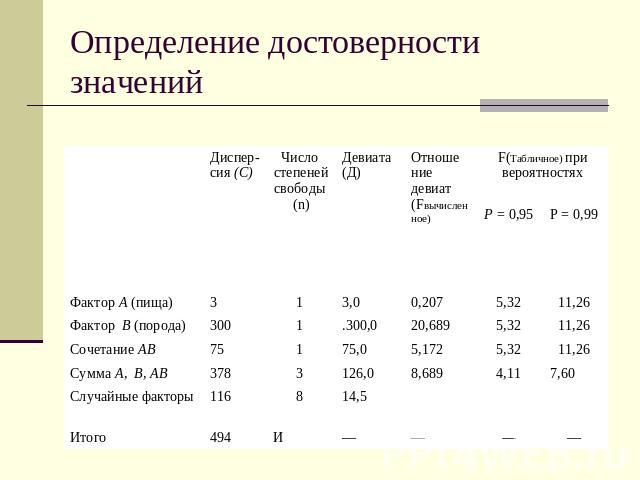
Определение достоверности значений

Спасибо за внимание!