Презентация на тему: Методы решения текстовых задач

Методы решения текстовых задач Слушатель ОП «Математическое образование в основной и средней школе» Шаронова Мария Викторовна

Содержание: Введение 31. Составные части задачи и требования по ее решению в школьномкурсе математики 42.Метод математического моделирования при решении текстовых задач. 62.1. Понятие модели и моделирования. 62.2. Моделирование при решении задач. 102.2.1.Задачи на встречное движение двух тел. 132.2.2.Задачи на движение двух тел в одном направлении. 142.2.3.Задачи на движение двух тел в противоположных направлениях. 152.3.Опытно-практическая работа по сопоставлению применяемых способов решения задач в 5 и 9 классов. 17 Заключение 18Приложение.Список литературы.

Методы решения задач - анализ и синтез- метод сведения к ранее решённым- метод математического моделировавния- метод математической индукции- метод исчерпывающих проб

Метод математического моделирования «В процессе математического моделирования выделяют три этапа: 1. Формализация – перевод предложенной задачи (ситуации) на язык математической теории (построение математической модели задачи). 2. Решение задачи в рамках математической теории (говорят: решение внутри модели). 3.Перевод результата математического решения задачи на тот язык, на котором была сформулирована исходная задача (интерпретация решения).»

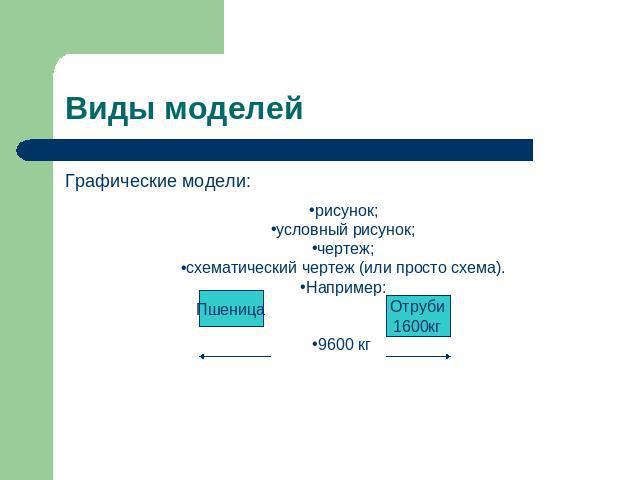
Виды моделей Графические модели:рисунок;условный рисунок;чертеж;схематический чертеж (или просто схема).Например:9600 кг

Знаковые модели: - краткая запись задачи;- таблица

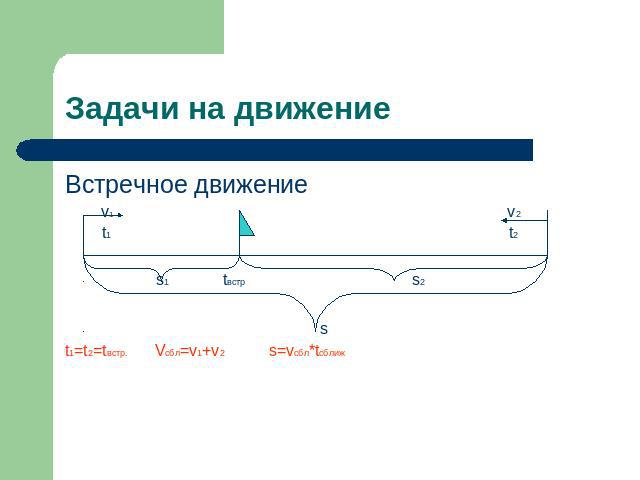
Задачи на движение Встречное движение v1 v2 t1 t2 s1 tвстр s2 st1=t2=tвстр. Vсбл=v1+v2 s=vсбл*tсближ

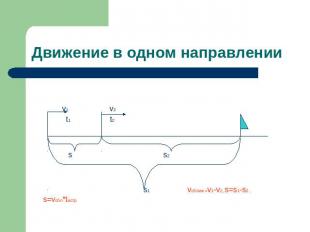
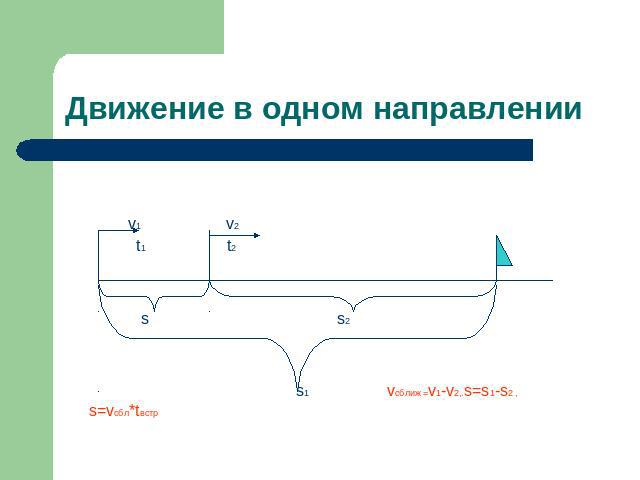
Движение в одном направлении

Движение в противоположных направлениях В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки: а) одновременно; б) в разное время. А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.Общим теоретическим положением для них будет следующее: v удал. = v1+ v2, где v1 и v2 соответственно скорости первого и второго тел.(Схематический чертеж строится аналогично предыдущим).

Заключение В школьном курсе нет четкого разделения методов, в том смысле, что авторы школьных учебников не дают напрямую схему какого либо метода. Поэтому, решая задачи любого типа, пусть даже наиболее удобным методом не стоит забывать о других способах её решения.