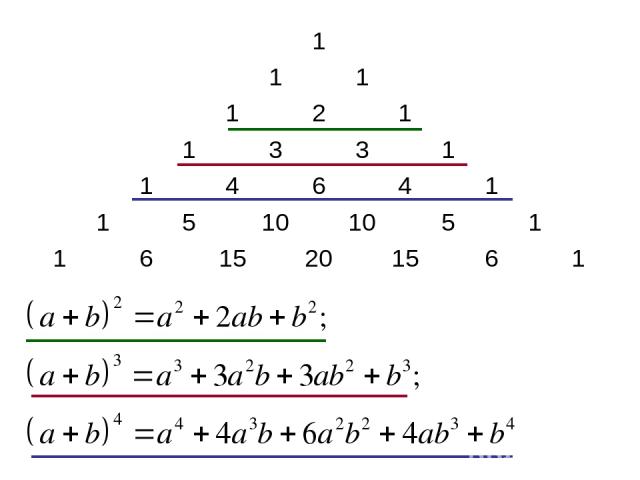Презентация на тему: Предел числовой последовательности

Числовые последовательности. Предел числовой последовательности. 1, 3, 5, 7, 9, 11… аn – общий член последовательности

Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7, 9, 6… Продолжите ряд 77, 49, 36, 18… Ответ: Перемножаются две цифры, входящие в предыдущее число Ответ: Ряд состоит из двух частей: числа на нечетных местах: 1, 3, 5, 7, 9...; числа на четных местах: 10, 9, 8, 7 Примеры последовательностей.

Назовем постоянной последовательность, если она равна константе для любого номера n:

Назовем последовательность ограниченной, если найдется такое число M, для которого модуль любого члена последовательности окажется не больше этого числа:

Последовательность ограничена, если найдется такое положительное число, для которого все члены последовательности по модулю окажутся не больше этого числа.

Последовательность называется возрастающей, если: Последовательность возрастает, если каждый последующий член не меньше предыдущего. Последовательность монотонная, если она возрастающая или убывающая.

Рукава многих галактик расположены в соответствии с этой последовательностью. Длины фаланг пальцев человека относятся примерно как числа Фибоначчи. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610… Числа Фибоначчи. Элементы числовой последовательности, в которой каждое последующее число равно сумме двух предыдущих чисел.

В сосновой шишке, если посмотреть на нее со стороны черенка, можно обнаружить две спирали, одна закручена против, другая по часовой стрелке. Число этих спиралей 8 и 13.

Когда потоки воды двигаются по океану и волны прилива подходят к берегу, они изгибаются в форме спирали, которая может быть математически отражена на графике с точками 1,1,2,3,5,8,13,21,34 и 55.

Ветви, листья деревьев, ракушки, морские звезды, ушная раковина человека, тюльпаны и другие цветы, и особенно раковины моллюсков - сформированы по той же самой схеме. С каждым приростом раковина добавляет себе ещё один сегмент в соответствии с масштабом Фибоначчи.    

Паук плетет паутину спиралеобразно по тому же принципу. Спиралью закручивается ураган...

Ячейки ананаса расположены в 8 правосторонних, 13 левосторонних, 21 вертикальных спиралей.

Семена подсолнуха располагаются в двух пересекающихся спиралях с количеством соцветий 34 и 55 или 55 и 89 согласно последовательности Фибоначчи.

Из истории астрономии известно, что И. Тициус, немецкий астроном XVIII в., с помощью этого ряда (Фибоначчи) нашел закономерность и порядок в расстояниях между планетами солнечной системы

Леонардо Пизанский или Фибоначчи Схемы, по которыми сформированы лепестки, листья и семена цветов, соответствуют определённым числам.

Леонардо Фибоначчи (родился около 1170 — умер после 1228), итальянский математик.

Последовательность Фибоначчи рекуррентно задать легко, а аналитически – трудно.

При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда  будет величина, колеблющаяся около иррационального значения 1.61803398875… . Божественная пропорция. Оказывается что число ФИ -Строительный камень, который господь Бог использовал для создания Мира.

Блез Паскаль (1623 – 1662 ). Французский математика XVII

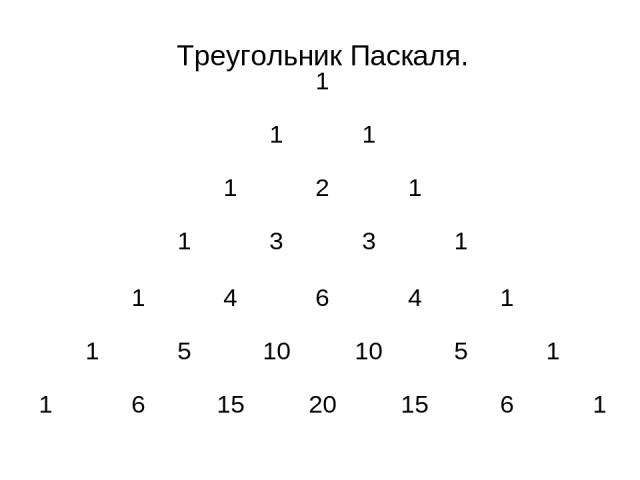
Треугольник Паскаля – это бесконечная числовая таблица треугольной формы, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа в предшествующей строке:

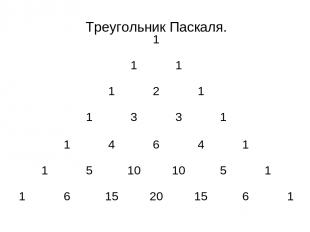
Треугольник Паскаля. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1

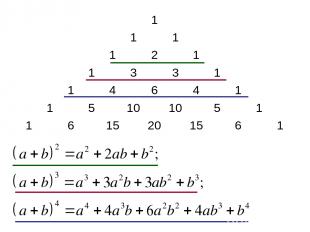
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1

1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1

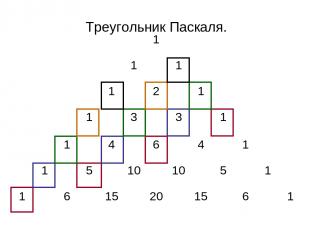
Треугольник Паскаля. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1

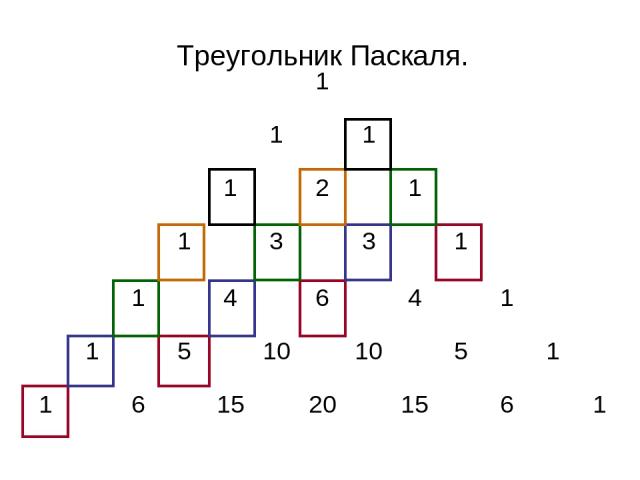
Подсчитав для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел, получим числами Фибоначчи : для 1 диагонали – 1; для 2 диагонали – 1; для 3 диагонали – 1+1=2; для 4 диагонали – 1+2=3; для 5 диагонали – 1+3+1=5; для 6 диагонали – 1+4+3=8; для 7 диагонали – 1+5+6+1=13 ….

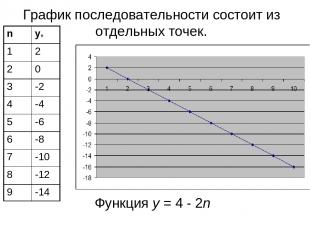
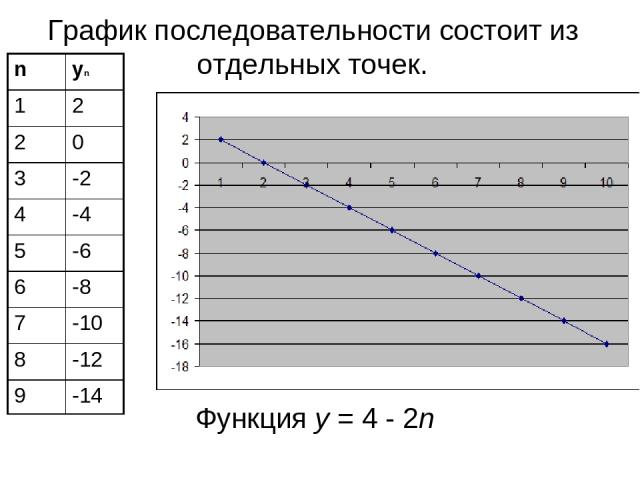
Функция у = 4 - 2n График последовательности состоит из отдельных точек. n yn 1 2 2 0 3 -2 4 -4 5 -6 6 -8 7 -10 8 -12 9 -14

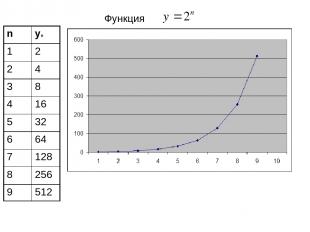
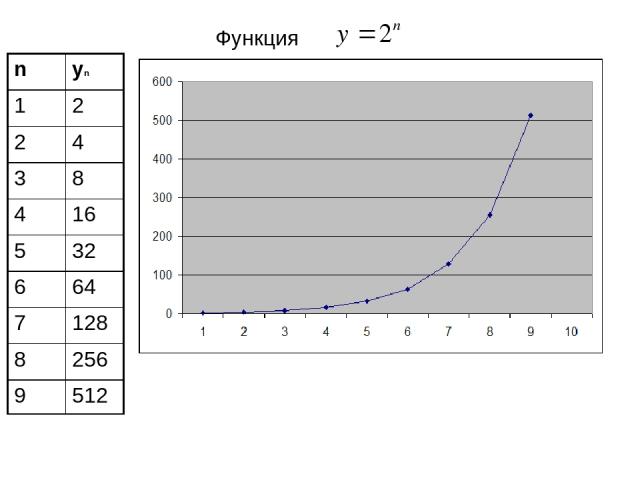
Функция n yn 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512

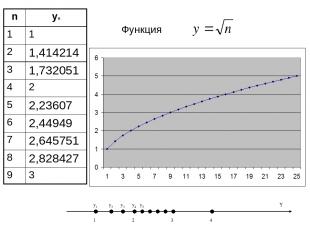
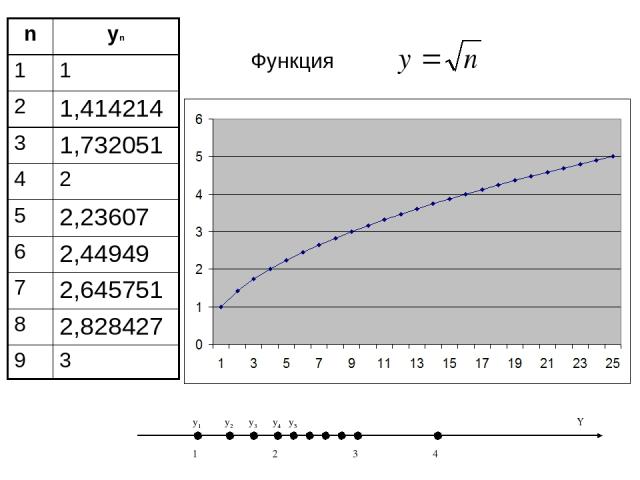
Функция n yn 1 1 2 1,414214 3 1,732051 4 2 5 2,23607 6 2,44949 7 2,645751 8 2,828427 9 3

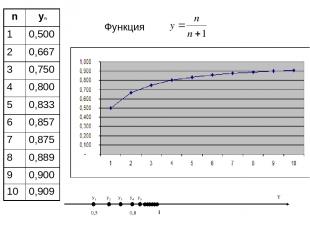
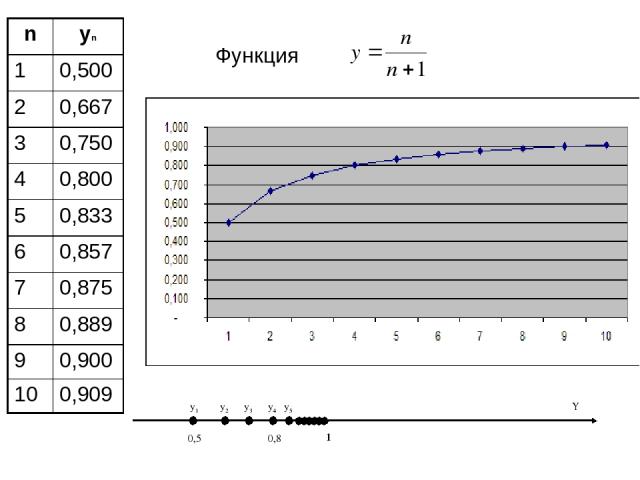
Функция 0,5 0,8 1 y1 y2 y3 y4 y5 Y n yn 1 0,500 2 0,667 3 0,750 4 0,800 5 0,833 6 0,857 7 0,875 8 0,889 9 0,900 10 0,909

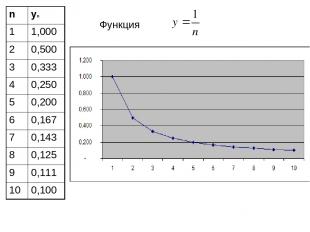
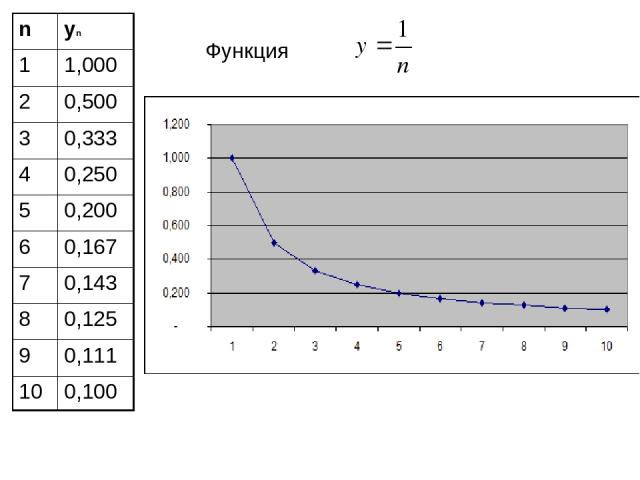
Функция n yn 1 1,000 2 0,500 3 0,333 4 0,250 5 0,200 6 0,167 7 0,143 8 0,125 9 0,111 10 0,100

Последовательность, которая имеет предел, называется сходящейся, в обратном случае последовательность расходится.

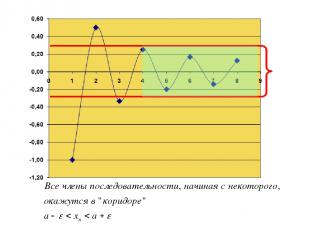
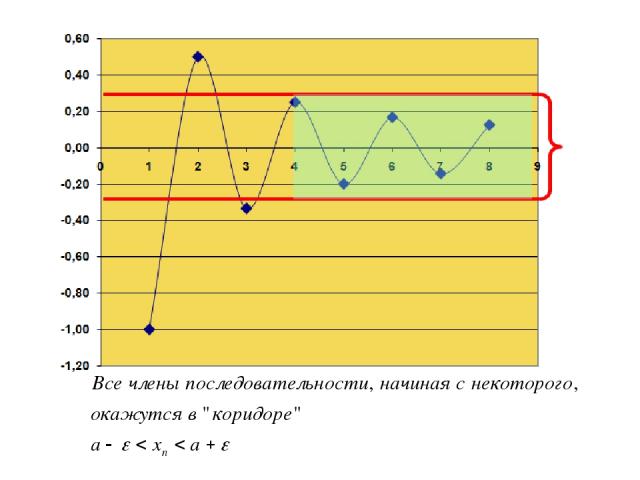
Число называется пределом последовательности x = {xn}, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |xn - a|

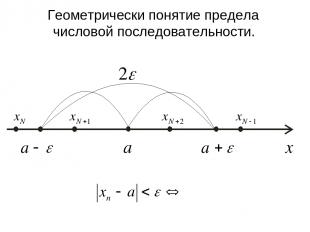
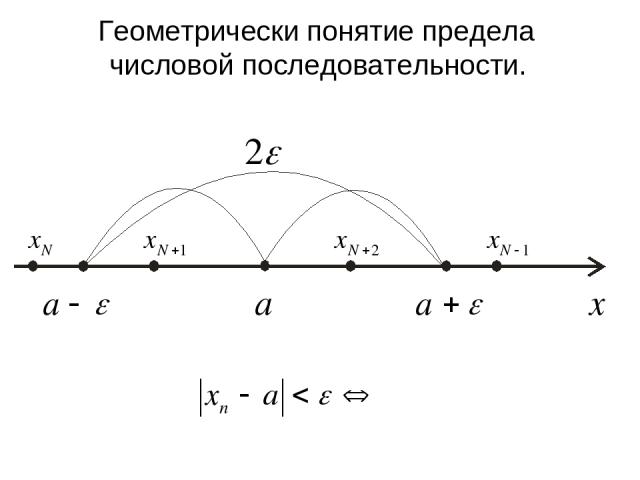
Геометрически понятие предела числовой последовательности.

Неравенство означает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ε; a + ε).

Постоянное число a есть предел числовой последовательности {xn}, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности точки a) найдется такой элемент последовательности с номером N, что все последующие элементы с номерами n>N будут находиться внутри этой окрестности.

Последовательность сходится, если она имеет предел.

Воспользуемся определением предела. По виду последовательности можно сказать, что с ростом номера n общий член последовательности хn приближается к единице, а разность |хn – 1| приближается к нулю.

Теорема о единственности предела последовательности: Последовательность не может иметь больше одного предела.

Это следует из того, что последовательность не может одновременно приближаться к двум разным числам одновременно. Формально, выберем ε значительно меньше разницы между числами a и b. Тогда очевидно, что мы не сможем указать такого номера N, начиная с которого одновременно будут выполнены два условия:

Теорема: Если последовательности {an} и {bn} сходятся, то сходится и их сумма {an + bn} и, кроме того, предел суммы равен сумме пределов:

Теорема: Постоянную величину можно выносить за знак предела:

Теорема: Если последовательности {an} и {bn} сходятся, то сходится и их произведение {an ⋅ bn} и, кроме того, предел произведения равен произведению пределов:

Теорема: Если последовательности {an} и {bn} сходятся, причем Предел отношения равен отношению пределов.

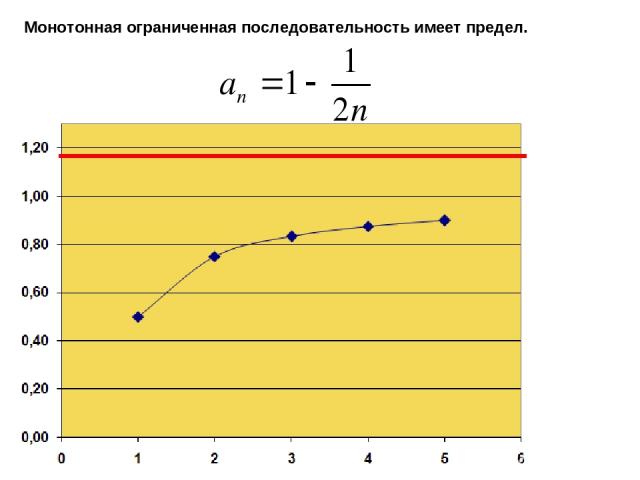
Теорема: Если последовательность ограничена и монотонна, то она сходится. Пример такой последовательности, которая ограничена, возрастает и потому имеет предел Признак существования предела.

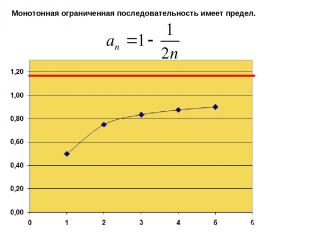
Монотонная ограниченная последовательность имеет предел.

Теорема о двух милиционерах Теорема (признак существования предела): Если одна последовательность заключена между двумя другими, имеющими одинаковый предел, то она имеет тот же предел. Название теоремы связано с такой ее интерпретацией. Если два милиционера ведут с двух сторон под руки подвыпившего гражданина и направляются в отделение, туда же придет и гражданин.

Дана последовательность

Ссылки на материалы из интернета: http://bmcapital.blog.ru/?page=5 http://forexaw.com/TERMs/Theory_of_market/l725_%D0%A4%D0%B8%D0%B1%D0%BE%D0%BD%D0%B0%D1%87%D1%87%D0%B8_Fibonacci http://sceptic-ratio.narod.ru/rep/kn15.htm http://geana.hiblogger.net/tag/%F2%E2%EE%F0%E5%F6/ http://www.skilpadde.ru/25-chisla-fibonachchi.html http://blog.i.ua/user/1577787/226447/ http://best-mama.info/publ/pochemuchka/biolog/34 http://kinder-online.ru/blog/lady-gaga-ili-njusha/page/2/ http://klen20078.ya.ru/replies.xml?item_no=3858 http://www.vlad-amelin.ru/stihi-o-zhizni/2256-zhizn-yeto-cep-sluchajnyx-chisel.html http://www.liveinternet.ru/users/daemaken/