Презентация на тему: Решение квадратных уравнений различными способами

Решениеквадратных уравненийразличными способами Автор работы:Уразгалиева Алсу, ученица 10 класса,МОУСОШ пгт Красная Поляна.Руководитель: Камаева И.Б., учитель математики

Цель работы: Знакомство с различными способами решения квадратных уравнений.Задачи: Подобрать информацию по теме из письменных источников и сети Интернет Составить план изложения материала по теме Законспектировать информацию Синтезировать информацию по плану Выбрать различные способы решений квадратных уравнений Составить разноуровневые карточки для самостоятельных работ Провести обобщение по теме.

Гипотеза: Предполагаю, что квадратные уравнения можно решить несколькими разными способами. Использование какого-либо способа зависит от индивидуальных особенностей человека, от его теоретической подготовки.Методы исследования: Подбор и обработка информации, знакомство с методами решения квадратных уравнений, подготовка дидактического материала по теме для учащихся 8 класса.

Квадратное уравнение – уравнение вида ax2 + bx + c = 0,где х- переменная, а,b и с-некоторые числа, причем, а ≠ 0. Если в квадратном уравнении ах2 + bx + c = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.Неполные квадратные уравнения бывают трёх видов:1) ах2 + с = 0, где b ≠ 0;2) ах2 + bх = 0, где с ≠ 0;3) ах2 = 0.

Из истории квадратных уравненийПравило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Индийский ученый Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:ах2 + bх = с, а > 0В уравнении коэффициенты, кроме а, могут быть отрицательными. Правило Брахмагупта по существу совпадает с нашим.

Формулы решения квадратных уравнений были впервые изложены в книге, написанной итальянским математиком Леонардо Фибоначчи(XIII в.).х2 + bх = с, при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Люди, благодаря которым способ решения квадратных уравнений принимает современный вид

Решение квадратных уравнений с помощью циркуля и линейки.Решим графически уравнение:x2-2x-3=0Решение: Определим координаты точки центра окружности по формулам:x= -b/2a= -(-2/2*1)=1y=(a+c)/(2a)=(1-3)/(2*1)= -1Проведем окружность радиуса SA, где А(0;1)Ответ: x1= -1; x2=3.

Решение квадратных уравнений с помощью номограммы. Номограмма- графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывание линейки) исследовать функциональные зависимости без вычислений.С помощью номограммы можно решить только приведенные уравнения, общая формула таких уравнений: x2+px+q=0

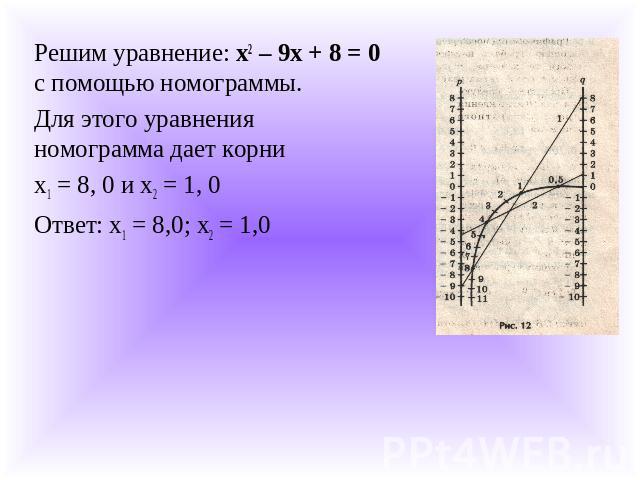
Решим уравнение: x2 – 9x + 8 = 0 с помощью номограммы.Для этого уравнения номограмма дает корни x1 = 8, 0 и x2 = 1, 0Ответ: x1 = 8,0; x2 = 1,0

Решения квадратных уравнений способом «переброски» Рассмотрим квадратное уравнение ах2 + bх + с = 0, а ≠ 0.Умножая обе его части на а, получаем уравнение а2 х2 + а bх + ас = 0.Пусть ах = у, откуда х = тогда приходим к уравнению у2 + by + ас = 0,равносильного данному.

Решим уравнение 2х2 – 11х + 15 = 0 .Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у2 – 11y +30 = 0.D=b2-4ac=(-11)2-4*30=121-120=1y1=(-b+√D)/2a=(-(-11)+1)/2*1=12/2=6y2=(-b-√D)/2a=(-(-11)-1)/2*1=10/2=5x1=y1/2=6/2=3x2=y2/2=5/2=2,5Ответ:x1=3 ; x2=2,5

ОбобщениеЗначение квадратных уравнений заключается в изяществе и краткости решения задач. В результате применения квадратных уравнений при решении задач обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений. Квадратные уравнения играют огромную роль в развитии математики. Моя работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.